基于SAT的可逆線路檢測集生成算法

李明翠，周日貴

（華東交通大學信息學院，江西 南昌330013）

能耗和散熱是電子產品功能越來越復雜、體積越來越小發展過程中日益突出的問題。由于可逆線路的低能耗特性，可逆線路被認為為未來量子計算、納米技術以及低功耗COMS等領域的一種解決方案。計算機每擦除一位信息就會釋放至少kT ln 2 J的熱量（k是波爾茲曼常數1.38×10-23，T是計算時的絕對溫度）［1］。不可逆電路中的能量消耗與在計算過程中擦除的信息位數乘正比。而可逆線路要求在計算過程中保持輸入和輸出的一一對應關系，因此可逆計算沒有信息丟失。Bennett［2］指出如果所有的運算都是用可逆部件完成的話，零能耗將成為可能。Barenco等［3］指出任何的運算在邏輯上和熱力學上都可以以可逆的方式進行。另一方面，由于量子物理學中的酉變換是可逆的，因此，可逆線路是量子力學中的最基本部分。從可逆門的設計到加法器及各種可逆電路的合成，國內外學者進行了很多相關的研究［4-7］。為了保證電路的正確性，在電路設計過程中和設計后的錯誤檢測非常重要。可逆電路的錯誤模型和檢測集生成方法與傳統電路存在很大的不同。目前提出的可逆線路錯誤模型主要有：固定點錯誤模型、單門失效模型、門重復錯誤模型、多門失效錯誤模型、門部分控制點失效等模型。Patel［8］提出的錯誤檢測集產生方法（ILP），Ramasamy［9］提出的基于錯誤表的適應樹方法，以及文獻［10-13］設計的基于奇偶保持的可逆容錯線路，都是針對可逆電路的固定點錯誤模型。然而，在可逆線路中，更能體現整個電路是否實現了目標功能的是門錯誤模型。Polian等人［14］用離子阱技術通過激光脈沖作用于離子的方式模擬了基于k-NOT 門的可逆電路的單門失效（SMGF）、門重復（RGF）、連續位置的多門失效（MMGF和門部分失效（PMGF）錯誤模型。Hayes等［15］提出了基于k-NOT 門的門失效錯誤模型（MGF）檢測方法DFT。DFT 方法是在原有線路中增加一條傳輸線和多個受控非門，這種方法的優點是僅用一個檢測向量就能檢測整個線路中是否存在單個門錯誤，但其缺點也很明顯：為了輔助錯誤檢測而增加的多個受控非門本身也可能產生新的錯誤，這些門一旦產生錯誤，DFT方法的優點將不復存在。肖芳英等人［16］提出了根據門間占據關系檢測單門失效的錯誤完備測試集算法CTS，這種方法不適于復雜的不規則電路。Zhang［17］提出了用向量反復迭代的方式獲得單門失效最小測試集的方法，其缺點是每生成一個測試向量都要用該向量對剩余錯誤進行迭代檢測。Kole［18］提出了連續位置門失效問題測試集的生成算法。以下根據SAT可滿足性原理著重研究基于k-NOT 門的可逆電路的單門失效錯誤檢測集的自動產生方法。

1 可逆電路中的單門失效錯誤模型

可逆電路的輸入和輸出具有一一對應的雙射關系，n位輸入的可逆電路必有n位輸出，常用n×n表示具有n位輸入和n位輸出的可逆電路。一個n×n的可逆電路的真值表具共有2n行輸入和2n行輸出。對于基本的二進制位輸入，可逆電路的輸出是輸入的某個排列置換。可逆電路從左到有對信息進行線性轉換，每向右邊增加一次轉換稱為深度增加1。k-NOT 門是組成可逆電路的最常用基本門。一個k-NOT門有k個控制位c1,c2,...ck和一個目標位t，實現的是一個(k+1)×(k+1)的酉變換。k-NOT 門的邏輯功能為即控制位的輸入與輸出相同，當所有的控制位的輸入都為1時，目標位的輸出與輸入相反。其中0-NOT 相當于一個反向器（NOT），輸出與輸入相反，1-NOT 也叫控制非門（CNOT），2-NOT 門也叫Toffoli門。圖1描述了這三種門的邏輯表示方式，其中門的控制位用·表示，目標位用⊕表示。

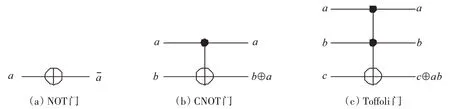
圖1 三種基本可逆門Fig.1 Three elementary reversible gates

單門失效錯誤（SMGF）指的是電路中的一個k-NOT門的功能完全消失，其所在位置相當于傳輸線直接連通的效果。實現該門的激光脈沖太短或者消失或沒有調整到位都可能是造成SMGF的物理原因。可逆線路具有非可逆線路所沒有的兩個重要特征可控制性和可觀測性。可控制性是指，存在一個檢測向量能產生電路中任意指定位置所需要的狀態，即在電路的某個深度指定的任意狀態都有一個對應的輸入向量。可觀察性指任何一個改變某個中間狀態的錯誤也同時改變輸出。根據可控性和可觀測性，一個SMGF可以通過設置失效門的所有控制點輸入為1，其他輸入是0或1來檢測。圖2（電路來源于可逆電路測試網站http：//www.cs.uvic.ca/～dmaslov）描述了虛線框中的2-NOT門失效的SMGF錯誤。在圖2的例子中，如果輸入{in1,in2,in3}={0,1,1}，正確的輸出應該是{out1,out2,out3}={1,0,0}，然而，當虛線框中的SMGF發生后輸出變成了{out1,out2,out3}={0,1,1}。線路中可能的SMGF數量與線路中門的數量相等。

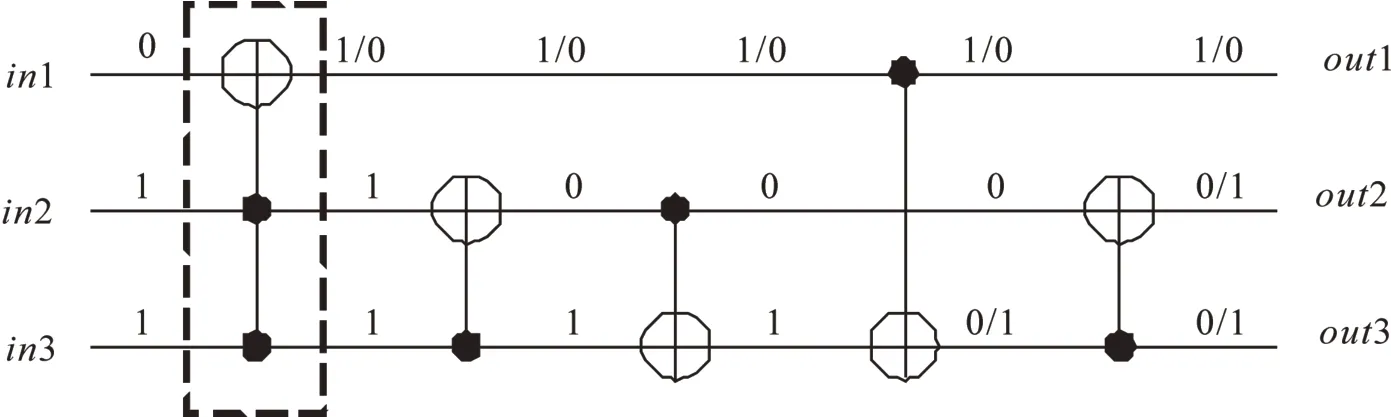
圖2 單門失效錯誤（SMGF）Fig.2 Single missing-gate fault（SMGF）

2 基于SAT的單門失效錯誤完備檢測集生成算法

布爾可滿足性問題（SAT）是指對給定的一個包含k個布爾變量的邏輯函數h，確定是否存在這n個變量的一組取值組合，使得h的值為1或者證明不存在使得h為1的取值組合。如果賦值組合存在則稱為可滿足（SAT），否則，稱為不可滿足（UNSAT）。SAT問題是計算機理論界和邏輯學界共同關注的重大問題，被廣泛的應用于自動規劃、模型診斷和電路等價性等方面的研究。SMGF問題可以轉化為這樣一個SAT問題“是否存在這樣一個輸入向量，使得k-NOT 門gj的所有控制位輸入為1，1 ≤j≤m，m是線路中的k-NOT 總數”。用NuSMV模型檢測器檢測指定的可逆線路是否滿足某個線性屬性。

2.1 可逆線路中的數據傳輸建模

給定一個具有n條傳輸線和m個k-NOT 門的可逆線路。假定所有的初始輸入為基本的二進制輸入0和1，則n位的0和1的組合沿著傳輸線從左到右依次經過m個可逆門進行傳輸和轉化。將電路中的n位數據用向量A=a1a2…an表示，A每經過一個k-NOT 門，狀態會發生改變，我們用aj i表示第i位數據經過第j個門后的狀態，用gj表示第j個門，1 ≤i≤n，1 ≤j≤m。則aj i的轉化可以用數學公式（1）描述。公式（1）表示n位信息經過gj后，只有gj的目標位所在的傳輸線中的信息會發生變化，其余信息位不變。

例如圖3中可逆線路Ham3中的信息轉化關系為

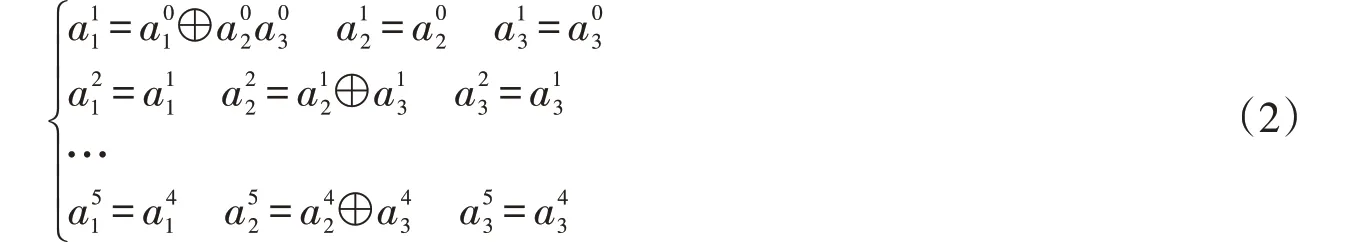
圖3 Ham3中的信息傳輸Fig.3 Data transformation in reversible circuit Ham3

2.2 SMGF錯誤約束

m個k-NOT 門組成的可逆線路有m個可能的SMGF錯誤。根據線路中門的輸入輸出關系，將m個可逆門生成m個數據轉化實例gc1,gc2,…,gcm。這m個實例的數據輸入輸出關系用公式（3）描述，其中gcj+1.in[i] ，是第j+1（1 ≤j≤m-1，1 ≤i≤n）個層次（深度）的輸入向量，gcj.out[i]是經過第前j個層次的k-NOT 門后得到的輸出。

一個SMGF的錯誤檢測可以約束為將該失效門的所有控制點輸入為設置為1。例如圖3中的編號為2的CNOT門的錯誤檢測約束為a13=1，即gc1.out[3]=1。同理編號為4的CNOT門的錯誤檢測約束為a13=1，即gc3.out[1]=1。公式（4）用線性時態邏輯（LTL）描述了第j+1個k-NOT門的錯誤約束的反，用來表示指定線路不存在滿足指定公式的屬性，其中p,q,…,r∈Cj+1，Cj+1是第j+1個k-NOT門的控制點集合。

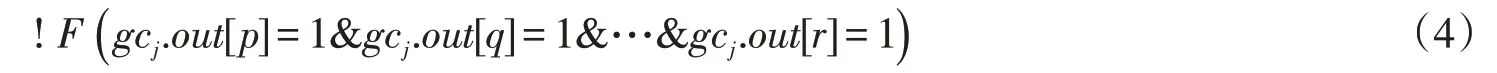
根據公式（4），圖3的Ham3線路中5個單門失效錯誤約束取反可以描述如下

將數據傳輸模型和錯誤約束LTL公式輸入SAT檢測器NuSMV，得到的反例就是每個錯誤的輸入檢測向量。Ham3 根據公式（1）～（5）得到的一組檢測集向量為（011，111，101，011，101），合并后得到（011，111，101），因此（011，111，101）是圖3所示Ham3的SMGF完備檢測集。

3 實驗結果分析

可逆線路單門失效錯誤檢測集生成算法實驗結果如表1所示。

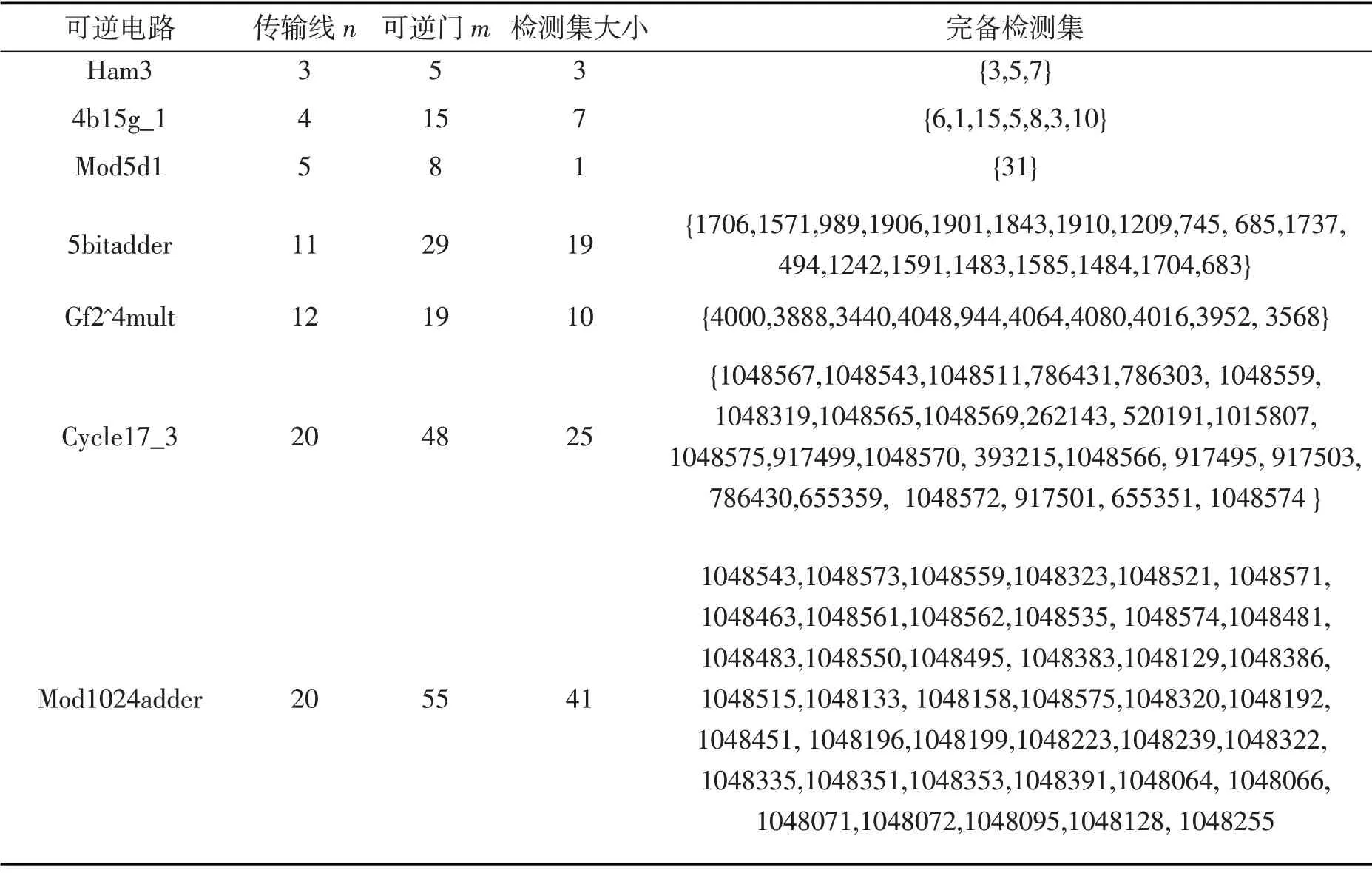
表1 文章所提出方法的實驗結果Tab.1 Experiment results of the proposed method

實驗所用線路全部來自可逆線路測試網站（http：//www.cs.uvic.ca/～dmaslov）。表中第1 列是所選用的可逆線路名稱，第2列是線路的傳輸線數目，第3列是線路中包含的可逆門數目，第4列是用本文提出的方法得到的完備檢測集大小，第五列是具體的檢測集，其中所有的檢測向量都已轉換為十進制數，其對應的二進制數從高位到低位對應于線路的傳輸線1,2,…,n的輸入。實驗結果顯示本方法對于無規則線路和復雜線路均有效。

在檢測過程中，由于NOT門可以被任意輸入向量檢測到，因此在檢測集生成時可以忽略NOT門的檢測向量生成。對輸入有特殊限制的電路（例如Mod5d1的最后一根輸入線要求是1，Gf2^4mult 的最后四根線的輸入要求為常量0），可以將錯誤約束LTL 公式進行特征約束擴展，將公式（4）擴展成公式（6），其中a0是電路最左端的初始輸入，u,...,v∈{1,2,3,...,n}是對輸入有特殊限制的傳輸線編號，w根據具體線路的輸入限制取0或1。

4 總結

可逆線路的可控制性保證了可以求得任意指定層次數據對應的原始輸入向量，可觀測性保證了任意層次數據的改變將直接反應到輸出結果。根據可控性和可觀測性，將檢測向量生成問題轉化為求解邏輯可滿足問題，通過在k-NOT 門的對應層次上指定其所有控制位輸入為1的約束條件來獲得對應的檢測向量。將邏輯線路的數據轉化抽象成線性邏輯公式，用線性時態邏輯LTL描述所求問題的反，通過求反例的方式來自動生成整個可逆電路的完備單門失效錯誤檢測集。用可逆線路網站上的部分線路檢測提出的方法，實驗結果顯示此方法能夠很好的產生完備檢測集，自動化程度高，能應對不規則的復雜線路，易于針對線路的特殊屬性進行擴展。

[1] LANDAUER R.Irreversibility and heat generation in the computing process[J].IBM Journal of Research and Development, 1961,5(3):183-191.

[2] BENNETT C H.Logical reversibility of computation[J].IBM journal of Research and Development, 1973,17(6):525-532.

[3] BARENCO A,BENNETT CH,CLEVE R.Elementary gates for quantum computation[J].Canadian Metallurgical Quarterly, 1995,52(5):3457-3467.

[4] TOFFOLI T.Reversible computing[M].Berlin Heidelberg:Springer,1980:1-34.

[5] THAPLIYAL H, SRINIVAS M B.A novel reversible TSG gate and its application for designing reversible carry look-ahead and other adder architectures[M].Berlin Heidelberg:Springer,2005:805-817.

[6] 黎海生,周日貴.在糾纏量子系統中的圖像幾何形狀存儲和檢索[J].華東交通大學學報,2013,30(4):14-18.

[7] ZHOU RIGUI,ZHANG MAN QUN,WU QIAN,et al.Optimization approaches for designing a novel 4-bit reversible comparator[J].International Journal of Theoretical Physics,2013,52(2):559-575.

[8] PATEL K N, HAYES J P, MARKOV I L.Fault testing for reversible circuits[J].Computer-Aided Design of Integrated Circuits and Systems,IEEE Transactions on,2004,23(8):1220-1230.

[9] RAMASAMY K, TAGARE R, PERKINS E, et al.Fault localization in reversible circuits is easier than for classical circuits[C]//Proceedings of the International Workshop on Logic and Synthesis,June 2004.

[10] SAFARI P, HAGHPARAST M, AZARI A, et al.A design of fault tolerant reversible arithmetic logic unit[J].Life Science Journal,2012,9(3):643-646.

[11] BOROUMAND S,HAGHPARAST M.A novel nanometric fault tolerant reversible associative memory cell[J].Australian Journal of Basic and Applied Sciences,2011,5(10):945-950.

[12] MITRA S K,CHOWDHURY A R.Minimum cost fault tolerant adder circuits in reversible logic synthesis[C]//VLSI Design(VLSID),2012 25th International Conference.IEEE,2012:334-339.

[13] ZHOU R G,LI Y C,ZHANG M Q.Novel designs for fault tolerant reversible binary coded decimal adders[J].International Journal of Electronics,2014,101(10):1336-1356.

[14] POLIAN I, FIEHN T, BECKER B, et al.A family of logical fault models for reversible circuits[C]//Test Symposium, 2005 Proceedings 14th Asian.IEEE,2005:422-427.

[15] HAYES J P,POLIAN I,BECKER B.Testing for missing-gate faults in reversible circuits[C]//Test Symposium, 2004 13th Asian.IEEE,2004:100-105.

[16] 肖芳英,陳漢武,李志強.量子電路中門失效錯誤的檢測方法[J].儀器儀表學報,2008,29(10):2084-2089.

[17] ZHANG H,FREHSE S,WILLE R,et al.Determining minimal testsets for reversible circuits using boolean satisfiability[C]//Africon.IEEE,2011:1-6.

[18] KOLE D K,RAHAMAN H,DAS D K,et al.Derivation of test set for detecting multiple missing-gate faults in reversible circuits[J].Computers and Electrical Engineering,2013,39(2):225-236.