廣義誤差分布下CVaR模型的股市風險研究

朱翔翔， 姚 儉

（上海理工大學 管理學院，上海 200093）

金融業管制的放松和金融自由化的發展導致了全球金融市場波動的加劇，金融機構面臨著日趨嚴重的金融風險.目前，金融市場風險測度的主流方法是由Morgan提出的風險價值VaR（value at risk）.該指標不僅被金融機構用于風險管理，而且被眾多金融監管組織作為風險評估的標準.巴塞爾銀行監管委員會還在“1996年巴塞爾修正案”中利用VaR所確定的市場風險來規定銀行及其它金融機構的資本充足率.我國學者杜海濤［1］在市場指數風險量度、單個證券的風險度量、基金管理人員績效評價及確定配股價格等方面運用VaR 方法，驗證了VaR 模型對風險的測度效果較好.盡管VaR 指標在實踐中得到廣泛的應用，但其本身存在著諸多的理論缺陷，如VaR 不滿足一致性風險測度理論中次可加性的公理，這使得基于VaR 的資產組合無法通過分散化投資降低投資風險［2］.因此，人們提出了許多不同的風險測度指標，其中，條件風險價值 CVaR（conditional value at risk）滿足一致性風險測度理論，在性質上優于VaR 指標［3］.同時，金融資產收益波動率的測度及其動力學特征的刻畫，對基于VaR，CVaR 指標的金融市場風險測度具有十分重要的理論意義.目前的理論研究中存在多種不同的模型描述方法可以用于刻畫金融資產收益波動率，究竟哪一種模型最適合我國股票市場的實際波動特征和風險狀況尚無定論.實證研究發現［4］，我國金融資產的收益率序列普遍不服從獨立同分布假設且不服從正態分布，存在著波動集聚（volatilityclustering）和厚尾（fat－tail）的特性，具有很強的自回歸條件異方差（ARCH）效應.因此，可以運用廣義自回歸條件異方差模型（GARCH 模型）對滬深300指數的波動率進行估計.另外，在采用極大似然估計GARCH 模型時，通常假定誤差服從正態分布，但此種假設不能反映我國金融收益序列的特征，一般可以通過假定收益率序列服從具有尖峰厚尾特征的分布，如廣義誤差分布（GED）來解決［5］.廣義誤差分布可以通過其參數的調整擬合出不同的分布形式，使用更為靈活，對數據分布的刻畫也更準確.

基于以上認識，本文通過運用GARCH 模型為我國股票市場收益的條件波動率建模，同時選擇對金融資產收益率分布典型特征具有較強描述能力的廣義誤差分布來刻畫滬深300指數收益率的分布特征.在此基礎上計算不同風險測度模型的風險價值VaR 和條件風險價值CVaR，并運用返回檢驗方法檢驗VaR 和CVaR 兩種指標的準確性，探討適用于我國股票市場的風險測度方法.

1 數據選取與檢驗

滬深300指數是由滬深證券交易所聯合發布的反映我國A 股市場價格波動和運行狀況的重要指數.選取滬深300 指數為研究樣本，選擇2005年1月4日至2012年6月29日的每日收盤價格指數，共計1 816個數據.估計時對指數數據進行自然對數處理，計算指數的日收益率

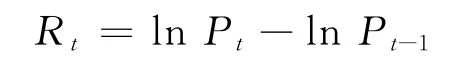
式中，Rt代表時間t 的日收益率；Pt代表時間t 的收盤價格指數.

圖1給出了2005年1月5日至2012年6月29日的每日收益率序列圖.從圖1中可以直觀地看出，收益率序列顯示出一定的波動聚集現象.

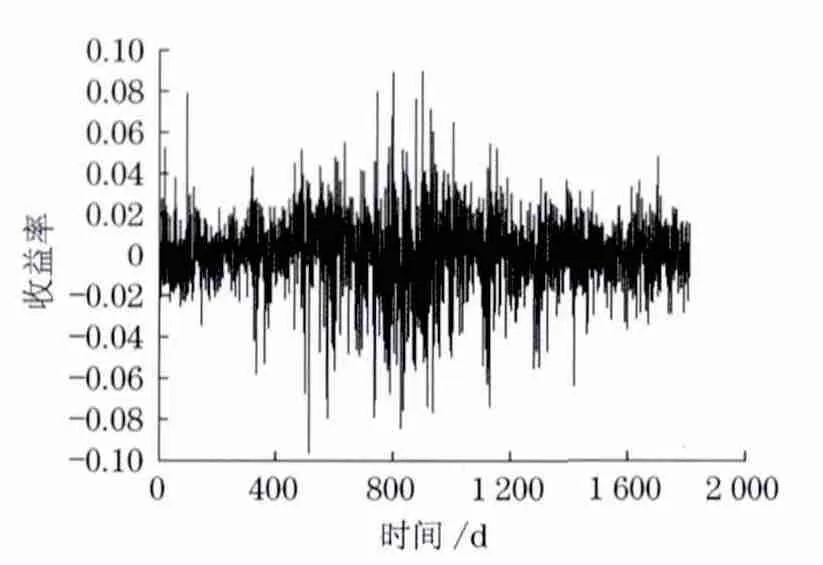
圖1 滬深300指數每日收益率序列Fig.1 Time series of daily return rate of CSI 300index

使用Engle 提出的拉格朗日乘數檢驗，即ARCH LM 檢驗，對原始收益數據進行ARCH 效應檢驗.表1為ARCH LM 檢驗結果.R 為可決系數，n為樣本量.

表1 異方差性檢驗：ARCH 效應Tab.1 Heteroskedasticity test：ARCH effect

表1中F 統計量和LM 統計量均十分顯著，說明拒絕收益序列沒有自相關的假設，暗示收益波動具有ARCH 效應，所以，可以利用GARCH 模型進行波動率的建模.

圖2將樣本數據頻率圖與正態分布對比，指數每日收益率呈現出明顯的尖峰厚尾現象，并不滿足正態分布的假設.

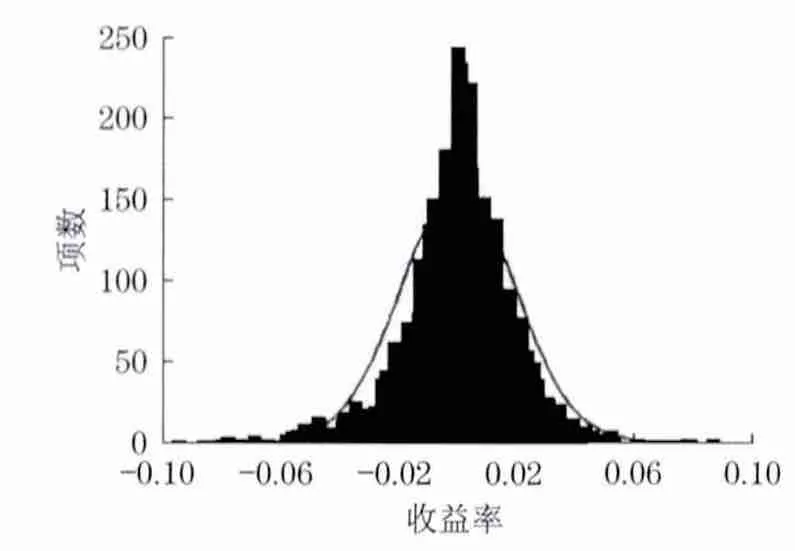
圖2 指數每日收益率分布與正態分布對比圖Fig.2 Comparison between return rate distribution and normal distribution

另外，運用迪基－福勒檢驗（ADF test）檢查數據的平穩性.從表2結果可以看出，收益率序列滿足平穩性假設，可以直接用于下一步的計量建模.

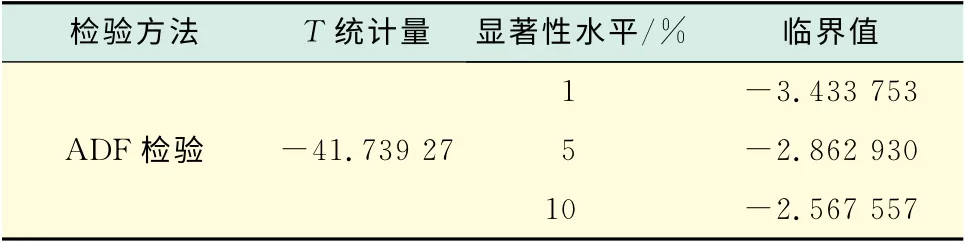
表2 收益率序列ADF單位根檢驗Tab.2 Unit root test of return rate series by ADFtest

2 我國股票市場波動率模型及估計

2.1 我國股票市場波動率模型

在金融時間序列中經常發生某一特征的值成群出現，即資產收益率大的變化（正的或負的）后，往往隨后會有大的變化，小的變化（正的或負的）后會發生小的變化，這就是波動聚集效應.圖1顯示，滬深300指數收益率具有明顯的波動聚集效應.針對這一現象，Engle 提出了自回歸條件異方差模型（ARCH 模型），很好地刻畫了金融時間序列的這種特征［6］.但由于在非負參數約束下求解極大似然估計，對參數進行估計有一定的困難，Bollerslev又提出了廣義的ARCH 模型，即Generalized ARCH 模型（GARCH 模型），他在條件方差的方程中加上了自回歸項，用簡單的GARCH 模型代表一個高階的ARCH 模型，彌補了ARCH 模型的不足，大大減少了待估的參數，使得方程更加簡約，避免了過度擬合［7］.Engle和Patton的研究結果表明［8］，實證研究中GARCH（1，1）模型是權衡計算精度和模型復雜程度的一種比較合適的折中，因此，現假定條件方差滿足GARCH（1，1）模型.

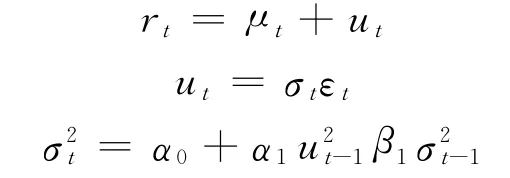
式 中，rt為 指 數 收 益 率；ut為 殘 差；μt 為 收 益 率 的 條件均值；εt為滿足獨立同分布且服從標準正態分布的隨機變量；α0，α1，β1 為系數.

考慮到我國滬深300指數收益率存在的尖峰厚尾現象（如圖2所示），采用一種較為靈活的、能夠同時刻畫這兩種特征的GED 來表示εt的分布情況.GED 的密度函數為

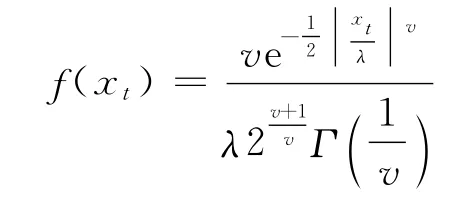
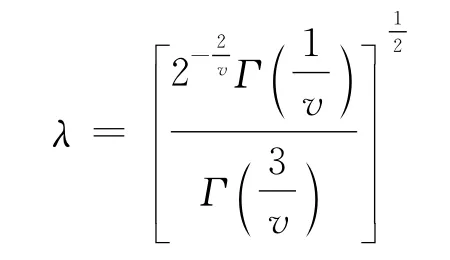
式中，Γ（ ）· 為伽馬分布；v為GED 分布參數.

通過對參數值v 的調整，GED 可以表示出不同程度的尖峰厚尾.當v＝2時，GED 即為標準正態分布；當v＜2時，廣義誤差分布比正態分布具有更厚的尾部和更尖的峰，而且隨著v值的減小，尖峰厚尾現象越明顯，即極端事件出現的概率隨v 的減小而增大；當v＞2時，其尾部則較正態分布更薄.

同時，為了驗證GED 分布假設對波動率方程估計的影響，還將對正態分布假設下的波動率方程進行估計.兩種不同的情況分別記為GARCH（1，1）－GED，GARCH（1，1）－N.

2.2 波動率模型的參數估計

運用Eviews軟件對兩種波動率模型進行參數估計，結果如表3和表4所示.

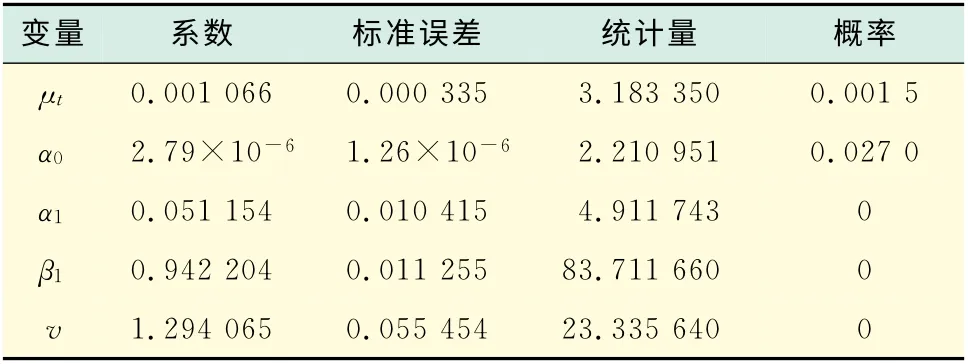
表3 估計GARCH（1，1）－GED 模型結果Tab.3 GARCH（1，1）－GED model estimation and results

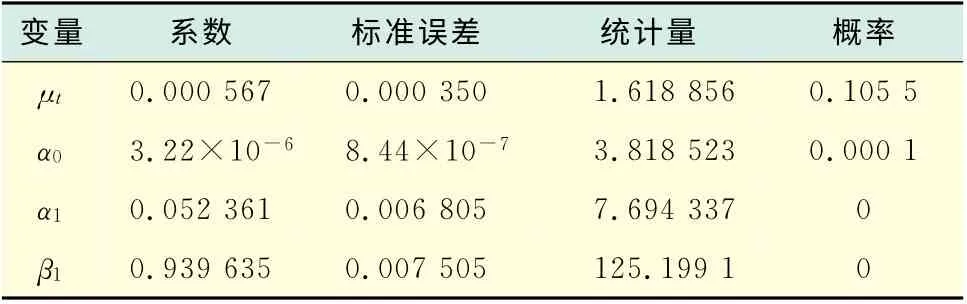
表4 估計GARCH（1，1）－N 模型結果Tab.4 GARCH（1，1）－N model estimation and results

從表3和表4的估計結果可以看出，條件方差方程中3項的系數均高度統計顯著.此外，與典型的金融資產收益GARCH 估計相似的是，這里滯后一期的誤差平方項與滯后條件方差系數的和接近于1.這表明沖擊對條件方差的影響具有很強的持續性.截距項μt 很小，而滯后條件方差系數β1 很大，為0.9，意味著在一段時間內，大的正或負收益會導致大的方差預測值［9］.

對GARCH（1，1）－GED 模型估計的殘差再作ARCH LM 檢驗，從表5（見下頁）的檢驗結果發現，殘差序列已經不存在顯著的異方差現象，所以，上述模型較好地刻畫了我國股票市場滬深300指數收益率序列的波動率特征.

表5 異方差性檢驗：ARCH 效應Tab.5 Heteroskedasticity test：ARCHeffect

3 風險測度值的計算及返回檢驗

3.1 風險測度值的計算

運用參數法計算VaR 值.在置信水平α 下，可以寫出t時刻的VaR 值為

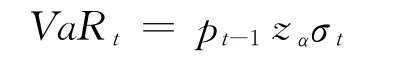
式中，pt－1代表滯后一期的指數值；zα表示在給定置信水平α 下的分位數；σt可由GARCH 模型先求出，進而開方得出相應的標準差σt.

取置信水平99%計算VaR 指標序列.

若用zα表示對應于某一置信水平α 的分位數，用q表示大于zα的分位數.根據CVaR 的定義可知CVaR 值為［10－11］

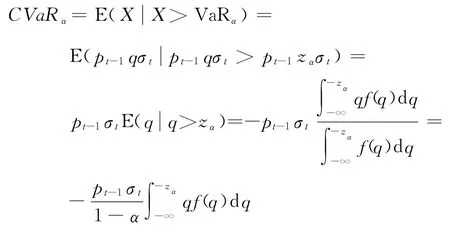
式中，pt－1表示第t－1日的指數收盤價格；f（q）表示收益率序列服從分布的密度函數.

在GED 條件下，CVaR 值為

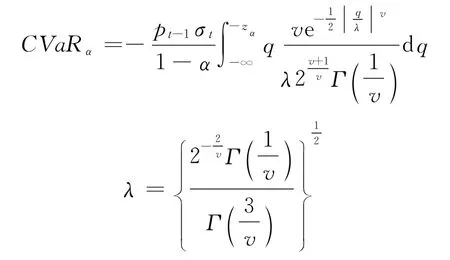
在正態分布條件下，CVaR 值為

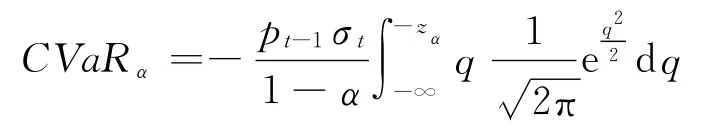
3.2 不同風險測度值的返回檢驗

對VaR，CVaR 進行返回檢驗分析主要是檢驗其對風險（實際損失）的覆蓋情況［12］.本文采用Kupiec于1995年提出的失敗頻率檢驗法.當損失超過風險測度值時，記為一次測度失敗，則失敗率PL＝N／T.其中，T 為實際考察天數，N 為失敗的天數.理論上每次觀察到的失敗次數服從概率為P＊L＝α的伯努利分布，所以，對風險測度值的檢驗便可以轉化為檢驗PL是否顯著等于P＊L.基于這一推論，Kupiec提出了似然比檢驗LR.

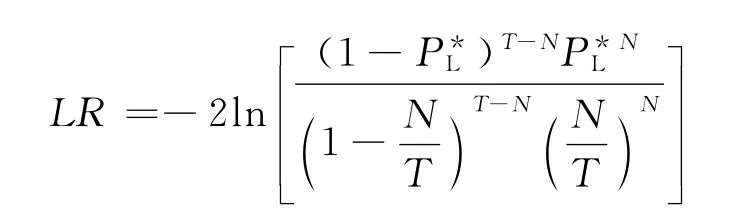
若零假設是正確的，則似然比滿足自由度為1的χ2分布，也就是說，在置信水平α上，如果所計算的LR 統計量大于該水平上自由度為1的χ2分布的臨界值，則應該拒絕原假設；反之，則應該接受原假設，即認為所采用的風險測度模型足夠準確［13］.

計算在99%的置信水平下基于GARCHGED 和GARCH－N 模型的兩種不同風險測度值.模型對風險狀況預測結果的返回檢驗采用最為常見的“失敗率”檢驗.由Matlab軟件計算，得到結果如表6所示.

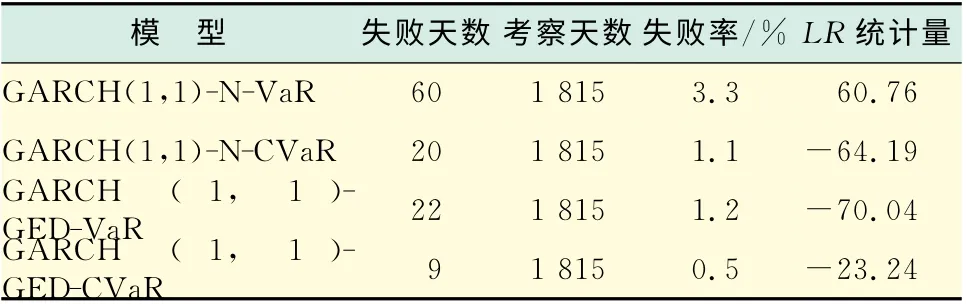
表6 99%置信水平下VaR，CVaR 模型的返回檢驗Tab.6 Back test of VaR and CVaR model at 99%confidence level

從表6的返回檢驗結果可知：a.基于GED 的兩種風險測度值均要好于基于正態分布的情況，因此，可以認為，目前研究中所采用的正態分布假設并不適用于我國股票市場的風險測度，而使用具有尖峰厚尾特征的GED 有助于提高對市場極端風險的估計精度.b.在99%置信水平下，基于相同的分布假定和GARCH 模型，CVaR 的失敗天數和失敗率均小于相應的VaR 的失敗天數和失敗率.由LR 統計量來看，只有GARCH（1，1）－N－VaR 模型未通過檢驗.其它3個模型的失敗天數均處于可接受的范圍內.因此，綜合考慮對我國股票指數收益率波動的刻畫以及VaR，CVaR 指標對風險的估計精度，結合GARCH（1，1）－GED 的CVaR 模型對我國股票市場的風險測度較為合理.

4 結 論

以滬深300指數為研究樣本，對我國股票市場指數收益率的波動特點進行了研究，結果表明，GARCH（1，1）－GED 模型可以很好地刻畫收益序列的波動率.在此基礎上對股市風險進行測度，實證分析了4種風險測度模型，并運用返回檢驗的方法對比了不同模型風險測度指標的精度，最終得出結論，在相同的收益率分布假定下，CVaR 指標對風險的測度更為準確、合理，說明CVaR 值對風險的容忍度更低，更加客觀保守，也更加符合風險管理的謹慎性原則，對我國金融市場的風險管理以及市場監管工作具有一定的借鑒意義.

［1］杜海濤.VAR 模型在證券風險管理中的應用［J］.證券市場導報，2000（8）：57－61.

［2］Artzner P，Delbaen F，Eber J，et al.Thinking coherently［J］.RISK，1997，10（11）：68－71.

［3］Artzner P，Delbaen F，Eber J，et al.Coherent measures of risk［J］.Math Fin，1999，9（3）：203－228.

［4］陳守東.VaR 的一種模擬方法［J］.決策借 鑒，2000，3（3）：32－33.

［5］吳曉霖，蔣祥林，孫紹榮.基于廣義期望效用理論的主觀概率調整的一致性風險測度［J］.上海理工大學學報，2010，32（5）：479－487.

［6］Engle R F.Autoregressive conditional heteroskedasticity with estimates of the variance of united kingdom inflation［J］.Econometrica，1982，50（4）：987－1008.

［7］Bollerslev T.Generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1986（31）：307－327.

［8］Engle R F，Patton A J.What good is a volatility model？［J］.Quantitative Finance，2001，1（5）：237－245.

［9］Brooks C.金融計量經濟學導論［M］.鄒宏元，譯.成都：西南財經大學出版社，2005.

［10］文鳳華，馬超群，陳牡妙，等.一致性風險價值及其算法與實證研究［J］.系統工程理論與踐，2004，24（10）：15－21.

［11］趙靜，肖慶憲.條件風險價值度量方法在銀行投資組合優化中的應用［J］.上海理工大學學報，2005，27（5）：389－392.

［12］王鵬，鹿新華，魏宇，等.中國金融期貨市場的風險度量及其Back testing分析［J］.金融研究，2012（8）：193－206.

［13］江濤.基于GARCH 與半參數法VaR 模型的證券市場風險的度量和分析：來自中國上海股票市場的經驗證據［J］.金融研究，2010（6）：103－111.