磁浮直線感應電機的PI 自適應電流可變轉差頻率魯棒控制

陳特放 鄧江明 唐建湘 成 庶 陳春陽

（1.中南大學信息科學與工程學院 長沙 410075 2.中南大學交通運輸與工程學院 長沙 410075）

1 引言

單邊直線感應電機（Single-sided Linear Induction Motor，SLIM）作為一種不經過中間傳動裝置，直接產生直線運動推力的具有優良控制性能的驅動設備，已經廣泛應用于磁懸浮、地鐵、工業機床、電動車門等領域[1]。同時，因為SLIM 結構的特殊性，它初、次級是開斷的，分別為:①短初級長次級結構應用于中低速控制領域，如日本的HSST—100L 磁浮系統，我國國防科大的CMS—04 試驗線、唐山試驗線、西南交通大學試車線[2]等；②長初級短次級結構應用于高速控制領域，如德國的TRANSRAPID 磁浮系統。SLIM 無輪軸和動力的機械轉換裝置，結構簡單、重量輕、體積小、運行可靠，使用起來安靜、無摩擦、污染小、散熱條件好、爬坡能力強[3]。正因為SLIM 的特有優勢和廣泛的工程應用價值，加上其結構及場量不平衡的特殊性，其運行的動態控制問題也是一直以來國內外學者的研究熱點。

目前國內外針對SLIM 運行控制的研究主要分為兩類:

（1）以文獻[4-6]為例的相關研究，以SLIM 的d-q 軸等效電路模型為基礎，由初級電流與磁鏈的坐標分解值計算電機的動態電磁推力，進而控制電機的運行速度。此類方法對直線電機的初次級電阻、電感參數要求已知且非時變。由于直線電機定轉子開斷導致特有的邊端效應，使得各類參數存在時變特性[7]，尤其是互感參數受入端行波影響較大，在高速時最為嚴重，增加了跟蹤及補償控制的復雜度。

（2）以文獻[8]為例的相關研究，采用了麥克斯韋（Maxwell）電磁場理論分析的方法證明了若控制SLIM 的定子電流與轉差頻率，就能有效地控制氣隙磁場與渦流場，也就能有效控制電機的推力與法向力[9]。這種控制方式因其不依賴直線電機的動態等效參數，如磁鏈、電阻等，控制方法簡單可靠，只需通過檢測電機電流與速度量，形成閉環矢量控制，被國內外學者廣泛用來控制磁懸浮列車，也即變流轉差（Variant-Current Constant Slip-Frequency，VCCSF）控制[10]。

鑒于VCCSF 方式帶來最大的問題是在某一恒定轉差下只能實現推力和法向力二者中的一個量最優（例如在磁懸浮應用中主要以實現法向力最優），這樣，不能充分利用直線電機的額定容量以輸出更大推力，從而實現磁浮列車的快速起制動。為解決推力和法向力的電流轉差頻率協同最優控制問題，本文先分析了最大推力輸出的轉差頻率與過零法向力的轉差頻率配置，針對兩個轉差頻率點不重合，提出了一種分段變轉差頻率變電流（Variant Current and Variable Slip-Frequency，VCVSF）控制方法。通過控制轉差頻率和電流的自適應調整，既能夠獲得較大的起動制動推力，同時在穩態運行工況下也可以實現法向力最小。此外，為了確保SLIM 在穩態運行時法向力振動的自收斂，以對抗電機內在干擾（各類橫向邊端效應）和外在干擾（軌道不平順），本文還建立了以穩態轉差頻率點波動為其中一個阻尼控制變量的Popov 超穩定模型，通過在線性環節增加前饋補償器的方式確保等價反饋系統嚴格正實，從而實現法向力輸出對懸浮系統的干擾最小。實驗不僅驗證了所提控制算法的有效性，還能細化研究SLIM 推力-法向力特性，為磁懸浮的高效動態優化控制提供參考。

2 分段變轉差頻率控制策略

2.1 推力最優點轉差頻率配置

因SLIM 開斷不對稱的結構特點，其在運行控制中存在兩類效應:橫向邊端效應和縱向邊端效應。因為中低速磁浮直線電機采用的是多極（單臺8 個），五臺換位級聯拓撲編組的方式運行，而且次級鋁導板的寬度大于初級鐵心磁場作用的有效寬度，在這種情況下，橫向端部效應對級聯電機組的影響已很小，國內外學者一般考慮的是與速度相關的動態邊端效應對電機力輸出特性的影響，并基于場路復量功率相等的原則，提出考慮動態邊端效應影響的SLIM 的T 形一相等效電路[4,5,11]，如圖1所示。

圖1 SLIM 的T 形等效電路（Duncan 模型）Fig.1 Duncan equivalent circuit model (ECM) of SLIM

圖1 中，電壓有效值為U1；r1、Llσ分別為初級電阻、漏感；Lm為互感；ω 為同步角速度，r′2/s 為折算后次級等效電阻；s 為轉差；L′2σ為折算后次級等效漏感。因動態縱向邊端效應引起的渦流和氣隙磁密在電機入端緩慢變化而在出端迅速衰減，故可只考慮入端行波的影響，對其補償通過修正勵磁電抗和在互感回路中串入附加電阻修正能量損耗。其中L′m=Lm(1-γ)，γ ˙為Duncan 修正系數[12]，計算如下:

式中 l——初級長度；

vm——SLIM 的瞬時速度。

圖1 中與速度變量有關的阻抗描述為

其中阻抗模值為

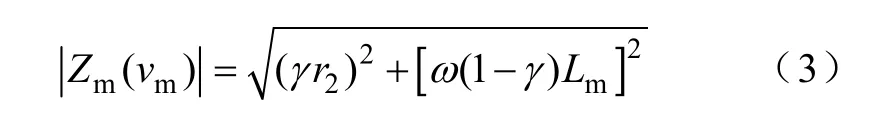
通常r2很小，同時γ＜1，故忽略式（3）右邊第一項，得

式中，ω=2πf1；f1為同步頻率，可得

由圖1，根據KVL 電壓定律，列寫電壓回路方程為

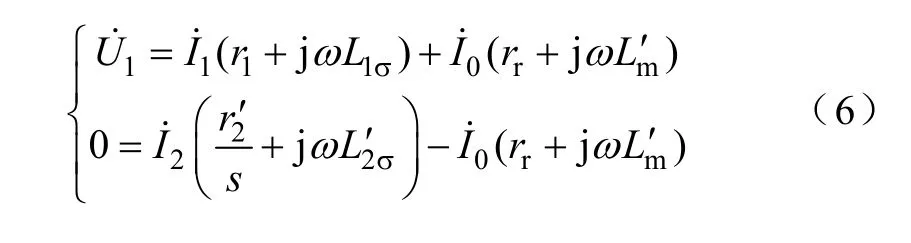
由基爾霍夫電流定理，A 點的相電流滿足

SLIM 同步電磁推力計算如下:

式中 Vs——同步速度，且Vs=2τf1；

τ——極距；

m1——初級繞組相數。

結合式（6）～式（8）可以得出

直線電機轉差頻率fs計算如下

故式（9）可化為

經驗證，由式（10）求得的fs，即為電機輸出推力最大時的轉差頻率，將式（12）代入到式（11）得到相應的最大推力為

式（11）表明，當控制fs為式（12）的值恒定不變時，電機輸出最大電磁推力，并且最大推力只與輸入電流有關，是輸入電流有效值的二次函數。

2.2 法向力最優點轉差頻率配置

SLIM 在運行過程中，電機初級與次級導電板及鐵軛渦流場的斥力、與次級鐵軛的吸力形成了電機在運行過程中所受的動態法向力。國內外學者給出了諸多不同法向力的推導與計算式[13-15]。本文引入基于二維多層通用行波理論[7,17]計算的法向力公式如下:

式中 k=π/τ；

D——電機有效寬度；

μ0——真空磁導率，取4π×10-7；

J1——初級行波電流層幅值，且

其中 Nph——每相串聯匝數；

kw1——電機繞組系數；

np——單個電機極對數；

G——直線電機的“品質因數”，且

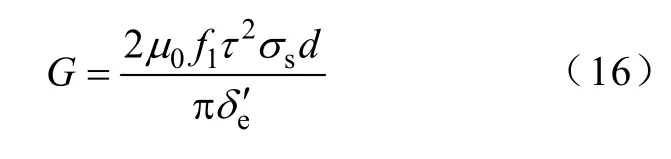
其中eδ'——電機等效氣隙；

d——次級導體厚度；

σs——次級導體表面電導率。

由式（10）、式（16），進一步得

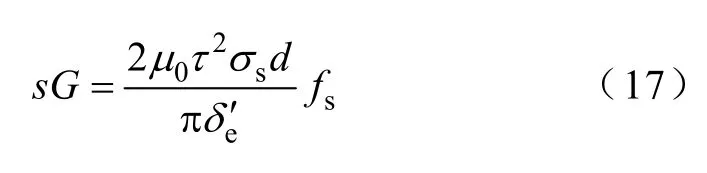
由式（14）、式（15）、式（17）可以看出，在其他參數恒定的情況下，若控制SLIM 的初級電流有效值I1和動態轉差fs，就可有效控制法向力。

由式（14），令Fy=0，可以得到法向力為零時，轉差頻率的最優控制點如下:

式中 ρs——次級體積電阻率，ρs=d/σs。

由式（12）、式（18）可知，因SLIM 按照設計方案成型后，推力最優點轉差fs,t與法向力最優點轉差fs,a通常不相等，有時相差較大。為了證明這一點，通過對一臺中低速（時速≤120km/h）磁懸浮用單邊短初級直線感應電機的額定設計參數（見表1、表2）進行相應計算。

表1 直線感應電機額定設計參數Tab.1 Design parameters of SLIM

表2 SLIM 等效電路參數列表Tab.2 ECM parameter list of SLIM

將表1、2 的各參數代入式（12）、式（18）中可得:fs,t=3.36Hz，fs,a=13.59Hz，顯然fs,t≠ fs,a。因此在恒電流變轉差頻率控制下無法在一個轉差控制點實現推力、法向力同步最優，故需研究分段轉差頻率控制策略，以解決電機推力和法向力協同優化控制問題。

2.3 分段可變轉差控制策略

結合式（12）、式（14）的表達式特性，可知SLIM 推力、法向力最優配置特性如圖2 所示。

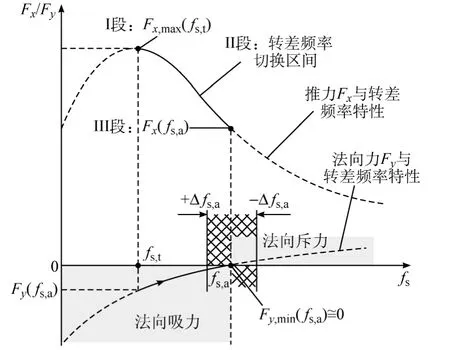
圖2 不同轉差頻率下SLIM 推力/法向力變化特性Tab.2 Analysis of thrust and normal force under the control of variable slip-frequency

若將轉差控制分為I、II、III 段，則可控制SLIM在加/減速段運行時，電機工作在某一轉差頻率點，使得推力輸出最優，電機以最短時間加減速；而在恒速段運行時，電機工作在另一轉差頻率點，使得法向力輸出最優，電機在法向不輸出對懸浮系統干擾的力矩。具體調節策略如下:

I 段-加速:維持推力最優點的轉差頻率運行，即控制fs=fs,t＜fs,a，SLIM 獲得較大的推力和加速度值，在最短時間內加速到指令速度，此段電機的法向力表現為吸力，在中低速磁懸浮方案中，此轉差頻率下產生的法向力數值相比于該點約30kN 懸浮力還是較小且逐漸削弱，可幾乎忽略其瞬態影響。

II 段-轉差頻率自適應切換:隨著速度接近給定速度值時，需控制轉差頻率以自適應方式切換到電機法向力最優點fs,a，即fs=fs,t→fs=fs,a，以便電機法向力對恒速運行的懸浮系統的沖擊擾動最小。

III 段-恒速運行:隨著轉差頻率過渡到fs=fs,a，法向力逐漸降低到零值點（介于法向吸力與法向排斥力之間）附近時，此時維持轉差頻率在fs,a，法向力在零值點附近波動fs∈{fs-Δfs,fs+Δfs}，推力亦下降到一定值后穩定。

3 基于Popov 穩定的PI 自適應控制

當SLIM 應用于中低速磁懸浮列車運行時，在轉差頻率的自適應調整策略上，要考慮以下兩方面:

（1）在垂直方向存在懸浮車體上下自由慣性沖擊，因F 軌道曲線特性，即使懸浮系統能在各種振動沖擊和電機法向力的影響下保持懸浮穩定，也會引起SLIM 氣隙的非線性波動[16]。從式（17）也可看出，sG(fs)是與電機氣隙有關的，這樣即使控制轉差率恒定在法向力最優點，法向力也會隨著氣隙的變化在零點處非線性波動，從而給懸浮系統帶來擾動沖擊，尤其當法向力與車體慣性基波發生共振時，嚴重時會導致懸浮失敗。

（2）氣隙和加速度類傳感器引入的反饋狀態控制信息，存在至少一個采樣周期的延時[17]，加上控制算法計算時間，故自適應魯棒控制系統的開環至少設計為二階。

綜上考慮，為保證在穩態最優點轉差處的法向力非線性振動自收斂，以實現法向力輸出對懸浮系統的干擾最小。先建立法向力控制電流ip(t) 與懸浮氣隙eδ'(t) 為狀態變量的二維狀態空間模型，然后取穩態轉差頻率fs(t) 為其中一個阻尼控制量的Popov自適應模型，則整個控制系統的等價非線性反饋部分分解如下:

（1）線性環節

（2）非線性環節

式中，A0、B0為時變參數矩陣的初始值，使式（20）滿足Popov 積分不等式的解為

取PI 型正定積分核:KΦ(t-τ)=KΦ＞0，KΨ(t-τ)=KΨ＞0，Ki(t)=Ki＞0，以實現狀態矢量x(t)平滑控制。根據超穩定理論，在非線性環節滿足Popov 不等式下，要求線性環節嚴格正實[18]，而線性環節狀態特性依賴給定的Am，而一般情況下要求Am嚴格正實是不太現實的，為此在前向通道中設置了線性補償控制器D，這樣即使已知的Am非正實，亦可通過調節D 來保證。整個自適應補償控制系統結構如圖3 所示。

圖3 基于狀態描述方程的Popov 穩定PI 自適應控制Fig.3 PI adaptive controller based on state space function

式（19）的等價反饋環節的前向矩陣表達式為

而式（21）描述的自適應系統，要求Gv(s) 必須是嚴格正實。由K-Y 引理[21]，必然存在一個對稱正定矩陣P 和一個對稱正定矩陣Q，使得下式成立

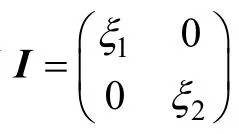
不失一般性，當Q 具有一般對稱正定矩陣表達形式，可采用Cholesky 分解，則P=M·M*，其中M 為主對角線上元素全為正的下三角陣，M*為其共軛轉置陣，則線性補償控制器D 求解為

式中，a11＞0，a22＞0，為M 矩陣主對角元素；Γ為實對稱部分。

可知反饋增益ξi影響D 矩陣的值，而D 矩陣的不同值決定了補償前向通道的比例增益，即決定非線性自收斂速率。

進一步討論所采用的PI 自適應控制律與傳統恒轉差頻率下的PI 電流控制在系統的時間響應特性上的表現。在理想的恒電流轉差頻率控制系統中，其二階離散型輸入輸出差分表達形式為

而PI 自適應控制律差分表達式為

式中，{yk}表示輸出時間序列，{uk}表示控制量采樣值序列，k 為當前時刻，k-1 表示上一時刻。ai、bi均為相應的二階和PI 控制系數，為常量。

對比式（25）、式（26），一旦采樣周期T 取值很小時（本文中數據采集周期500μs 遠小于控制采樣周期100μs），在此時間段內可認為輸入量保持著與前一個采樣時刻一樣的值

則在輸出時間序列上，采用本文的控制算法就可少計算了一步反饋狀態值ayk-2。即使忽略ayk-2的作用時間，也可通過合理選擇積分核參數KΦ、KΨ的值，使得PI 自適應算法在控制時間響應特性上不比傳統恒轉差PI 電流算法表現差。

圖4 實驗平臺和DSP 控制器內部算法設計Fig.4 Laboratory platform and DSP controller design block diagram

4 實驗研究

算法的實用性在一個轉向架含兩臺牽引直線電機的磁浮小車上予以驗證，實驗平臺及控制器結構原理如圖4 所示，采用C 語言編程在微處理器DSP–TMS320F2812 上實現所提控制算法；小車支撐軌道結構為F 型軌，表面為厚4mm 的鋁板，鐵軛為厚28mm 的Q—235 導磁鋼材質，牽引用直線感應電機采用雙層疊繞的方式，符合JB/T 7823—2007 標準，初級相數為三；最大設計時速不大于120km/h，初級額定電流340A，電機的U、V、W 端連接到IPM逆變器模塊輸出端，IGBT 開關頻率10kHz，懸浮控制采用直流斬波控制器輸出可變直流，穩定懸浮間隙在8mm 左右，其中電機的各個參數見表1，實驗供電電源±DC750V，考慮到γ 隨速度的變化曲線，如圖5 所示，電機速度vm升高，SLIM 受動態邊端效應的影響，氣隙磁場逐漸削弱，式（13）中動態邊端效應因子γ 值變大，此時在恒定初級電流340A下，推力則逐步下降。為動態反映式（11）表現的推力受γ 的影響，在控制上既可以通過補償控制初級注入電流實現，也可以通過補償轉差頻率實現，因本文考慮的是變轉差頻率控制，故采用對轉差頻率的補償代替對電流的補償控制，這樣可以維持控制電流在額定值340A 以下運行。綜上分析，尋優計算的推力最大轉差頻率fs,t=3.65Hz（低速區補償γ-0.29Hz）和法向力過零點轉差頻率 fs,a=15.65Hz（高速區補償γ-1.96Hz），逆變器輸出最大同步頻率fup=39.4Hz，因為測試軌道長小于30m，且小車慣性較大，加速時間和距離較長，從測試安全的角度出發，將小車的速度和加速距離統一折算到一個單位時間（約8.66s），它反映了電機在安全距離內將單位質量加速到給定速度所需的時間。整個測試分為三步:①測試電機在VCCSF 策略下的性能；②測試電機在VCVSF 策略下的性能；③測試電機在法向力為零處電機的受線性補償矩陣變量 Di的影響法向力振動自收斂特性表現。本文研究的前兩步控制分加速段，取控制指令速度v*（3m/s→8m/s）和減速度段，取控制指令速度v*（8m/s→3m/s）予以分析；而最后一步在穩定速度下，控制轉差頻率恒定在15.65Hz 時加以驗證法向力的自收斂特性。

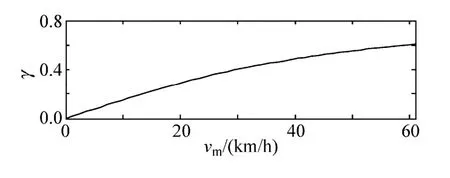
圖5 邊端效應因子γ 隨電機速度變化曲線Fig.5 Eddy-effect factor γ˙ versus motor speed

圖6、圖7 分別為電機在VCCSF 策略下的電機加速、減速狀態下的速度vm、三相電流iabc、轉差頻率fs、推力Fx和法向力Fy動態波形。從圖中可知，在0.2s 時，上位機發出加、減速控制指令，電機隨即加、減速。控制在法向力最優點的恒定轉差頻率15.65Hz 下，電機維持法向力在零值點附近，此時推力最大輸出只有約±2 300N，而在PI 電流調節器作用下，電流被限幅輸出340A，因為速度上升慢，電流外環調節時間較長，電機的跟蹤時間也較長，在一個單位時間里，電機無法以足夠的精度跟蹤到給定值。

圖6 恒轉差頻率PI 電流調節下各加速動態波形Fig.6 Acceleration waveforms under VCCSF control

圖7 恒轉差頻率PI 電流調節下各減速動態波形Fig.7 Deceleration waveforms under VCCSF control

圖8、圖9 分別為電機在VCVSF 策略下的電機加速、減速狀態下的速度vm、三相電流iabc、轉差頻率fs、推力Fx和法向力Fy動態波形。從圖中可知，在0.2s 時，上位機發出加、減速控制指令，電機隨即加、減速。在小于0.5 個單位時間里，電機快速跟蹤到給定值。因為采用先變轉差頻率的原則，電機轉差頻率從15.65Hz 下將至3.65Hz，且先維持電流在最大幅值 340A 處運行，則此時電機產生約4100N 大推力（比VCCSF 策略大了近78%），極大縮短了電機加速時間，而法向力體現為吸力作用，約為1600N，然后隨著轉差頻率上升，逐步下降。當電機速度接近指令值，轉差頻率以PI 平滑跟蹤形式升至15.65Hz，從而繼續維持法向力在零值點附近，而推力輸出此后在PI 自適應電流調節下，由340A 下降到與負載力矩平衡，完成整個加速/制動過程。

圖8 變轉差頻率PI 電流調節下各加速動態波形Fig.8 Acceleration waveforms under VCVSF control

圖9 變轉差頻率PI 電流調節下各減速動態波形Fig.9 Deceleration waveforms under VCVSF control

表3 給出的是兩種控制策略下的速度跟蹤性能統計，其中閾值點ε=|v*-vm|/v*×100%，本文取ε=10%，ε=5%，ε=1%三個點予以分析，對比表3的數據可以看出，VCVSF 策略在速度跟蹤的動態響應上要比VCCSF 策略表現好，是因為變轉差頻率輸出推力比恒轉差頻率輸出的推力大的緣故。

表3 兩種控制策略跟蹤快速性能統計Tab.3 Tracing performance statistics of studied two algorithms

為了簡化PI 積分核參數的整定，根據轉差頻率和初級電流各自的額定值限制，先取K1=K3=0.075，然后經多次試湊，在相對最好的輸出動態特性下，整定得到K2=1.26，K4=16.3。其中，控制采樣周期T=100μs，各參數矩陣求解如下:

圖10 給出的是電機分別在不同線性矩陣Di控制下，法向力過零轉差15.65Hz 處振動自收斂特性。表4 為不同Di下相應的狀態量統計，從表中可知，雖然線性補償矩陣列二范數||D2||2＞||D1||2＞||D0||2，自適應系統前向通道環節比例增益值越大，轉差頻率切換阻尼作用大，法向力自收斂速度也越快，但增加了占空比調節寬度，使得轉差頻率輸出波動范圍較大，而逆變器的實時頻率 f1(t)=fs(t)±|Δfs(t)|+vm/2τ，也加大了IGBT 的切換次數和損耗。故需綜合考慮，選取合適的D 參數，既實現快速的法向力自收斂速度，又可保證IGBT 切換次數不至過多，延長其使用壽命。

圖10 不同線性矩陣Di下的法向力自收斂特性Fig.10 Asymptomatically stable of Fyunder different Di

表4 不同矩陣值Di下自適應系統動態控制量r(t)邊界特性Tab.4 Boundary performance statistics of control variables r(t) under different linear matrix Di

5 結論

本文研究了一種將磁浮直線電機推力/法向力協同控制的變電流變轉差頻率控制方法，并通過建立以穩態轉差頻率為其中一個動態阻尼控制量的Popov 超穩定模型，在反饋線性環節增加補償器確保等價反饋系統嚴格正實，從而實現穩態運行時法向力振動的自收斂。理論與實驗均驗證了所提算法的有效性。以本文的研究為基礎，相關學者可以探索出直線電機的優化設計方案，使得推力法向力最優點轉差頻率兩個點能盡可能靠近，這樣可解決在一個轉差頻率點實現推力法向力同步最優的問題。

[1]佟力華,馬沂文,胥刃佳.適用于城市交通的中低速磁懸浮技術[J].電力機車與城軌車輛,2003,26(5):4-6.Tong Lihua,Ma Yiwen,Xu Renjia.Medium and low speed maglev technology applicable to urban mass transit [J].Electric Locomotives &Mass Transit Vehicles,2003,26(5):4-6.

[2]李希寧,佟來生.中低速磁浮列車技術研究進展[J].電力機車與城軌車輛,2011,34(2):1-4.Li Xining,Tong Laisheng.Technology research of medium and low speed maglev train[J].Electric Locomotives &Mass Transit Vehicles,2011,34(2):1-4.

[3]Yan L G.Development and application of the maglev transportation system [J].IEEE Transactions on Applied Superconductivity,2008,18(2):92-98.

[4]Faiz J,Jafari H.Accurate modeling of single-sided linear induction motor considers end effect and equivalent thickness[J].IEEE Transactions on Magnetics,2000,36(5):3785-3790.

[5]Kim D,Kwon B.A novel equivalent circuit model of linear induction motor based on finate element analysis and its coupling with external circuits[J].IEEE Transactions on Magnetics,2006,42(10):3407-3409.

[6]Xu W,Jian G Z,Zhang Y C,et al.An improved equivalent circuit model of a single-sided linear induction motor[J].IEEE Transactions on Vehicular Technology,2010,59(5):2277-2289.

[7]龍遐令.直線感應電動機的理論和電磁設計方法[M].北京:科學出版社,2006.

[8]Morizane T,Tsujikawa K,Kimura N.Control of traction and levitation of linear induction motor driven by power source with frequency component synchronous with the motor speed[J].IEEE Transactions on Magnetics,2011,47(10):4302-4305.

[9]Isfahani A H,Ebrahimi B M,Lesani H.Designoptimization of a low-speed single-sided linear induction motor for improved efficiency and power factor[J].IEEE Transactions on Magnetics,2008,44(2):266-272.

[10]Wallace A K,Parker J H,Dawson G E.Slip control for LIM propelled transit vehicles[J].IEEE Transactions on Magnetics,1980,16(5):710-712.

[11]Duncan J.Linear induction motor-equivalent circuit model[J].IEE Proceedings B–Electrical Power Application,1983,130(1):51-57.

[12]Ram P B,Dale R S.Thrust expressions for induction motors thin conducting secondaries[J].IEEE Transactions on Magnetics,1990,26(2):1101-1106.

[13]Laporte B,Takorabet N,Vinsard G.An approach to optimize winding design in linear induction motors[J].IEEE Transactions on Magnetics,1997,33(2):1844-1847.

[14]Lee B J,Koo D H,Cho Y H.Investigation of linear induction motor according to secondary conductor structure [J].IEEE Transactions on Magnetics,2009,45(6):2839-2842.

[15]Kuijpers A A,Nemlioglu C,Sahin F,et al.Force analysis of linear induction motor for magnetic levitation system[C].14th International Power Electronics and Motion Control Conference(EPE-PEMC),2010:17-20.

[16]Itoh K,Kubota H.Thrust ripple reduction of linear induction motor with direct torque control[J].IEEE Transactions on Magnetics,2007,43(5):655-658.

[17]Lin F J,Wai R J,Chou W D,et al.Adaptive backstepping control using recurrent neural network for linear induction motor drive[J].IEEE Transactions on Industrial Electronics,2002,49(1):134-146.

[18]Lian K Y,Hung C Y,Chiu C S,et al.Robust adaptive control of linear induction motors with unknown endeffect and secondary resistance[J].IEEE Transactions on Energy Conversion,2008,23(2):412-421.