一種具有頻率變化適應性的并網逆變器改進型重復控制方法

陳 東 張軍明 錢照明

（浙江大學電氣工程學院 杭州 310027）

1 引言

隨著近年來新能源的不斷發展和利用，應用于新能源的分布式發電系統受到了廣泛的關注和研究。而并網逆變器則是其中的一個重要組成部分。

為了減小對電網的污染，并網逆變器必須提高其輸出功率因數，減小其輸出電流的總諧波失真（Total Harmonic Distortion，THD）。為此多種針對并網逆變器的現代控制策略及算法已被提出，其中基于內模原理[1]的重復控制技術，在基波和諧波頻率處具有很高的增益，因此能夠使系統實現優秀的穩態跟蹤性能，和極低的THD[2-9]。然而，傳統重復控制要求系統采樣頻率與電網頻率的比值必須為整數。但此比值在某些應用場合中不能保持為整數，例如:①電網頻率存在波動，尤其是在分布式發電系統中較為明顯；②微控制單元的時鐘頻率為40MHz，采樣頻率為此頻率的整數倍分頻，如10kHz，而電網頻率為60Hz。此時若采用傳統的重復控制技術，由于其諧振頻率偏離了電網實際的基波與諧波頻率，系統的性能將會有顯著的降低。

文獻[10,11]提出了一種采用可變一階低通濾波器的重復控制方法，以適應電網頻率的變化。雖然該方法能使重復控制的諧振頻率在電網基波處完全吻合，但是其余的諧振頻率在諧波處還是有所偏離，導致其諧波抑制能力的下降。文獻[12]提出了一種采用虛擬采樣的重復控制方法，由固定采樣頻率的實際采樣數據經過線性插值法[13]得到虛擬采樣點的數據，并保持虛擬采樣頻率與電網頻率的比值為整數。但是該方法每個虛擬采樣點位于前后實際采樣點之間的位置不同，導致每次線性插值法的計算不同，提高了設計難度；同時變化的系統采樣頻率對數字控制系統的性能也存在一定的影響。

為了解決上面提到的問題，本文提出了一種改進型重復控制方法，它包含了一個基于線性插值法[13]的數字濾波器，與重復控制必需的延時環節相級聯。此數字濾波器能夠逼近于由系統采樣頻率與電網頻率比值小數部分構成的延時環節，從而使重復控制的諧振頻率與電網實際的基波及諧波頻率相吻合。當電網頻率變化時，本文提出的方法可以通過快速調整此數字濾波器的參數，保持其重復控制環節逼近于理想重復控制，從而顯著提高并網逆變器系統的穩態跟蹤性能和諧波抑制能力，實現了系統對電網頻率變化的適應。本文分析了此數字濾波器的特性以及該方法的原理，并且通過Matlab 軟件中的Simulink 仿真以及一臺三相并網逆變器樣機的實驗，驗證了該方法的有效性。

2 系統結構與模型

本文的研究主要在三相并網逆變器系統中進行，此系統的控制框圖如圖1 所示。該系統的功率部分由三相逆變橋，三相LC 濾波器（Lf和Cf），電路斷路器以及三相電網接口電感Lg組成。

圖1 三相并網逆變器系統控制框圖Fig.1 Control diagram of three-phase grid-connected inverter system

當三相電網電壓對稱且平衡時，選取兩個電感的電流iL、ig以及電容的電壓vC作為狀態變量，可以得到此系統在靜止坐標系下的狀態方程為

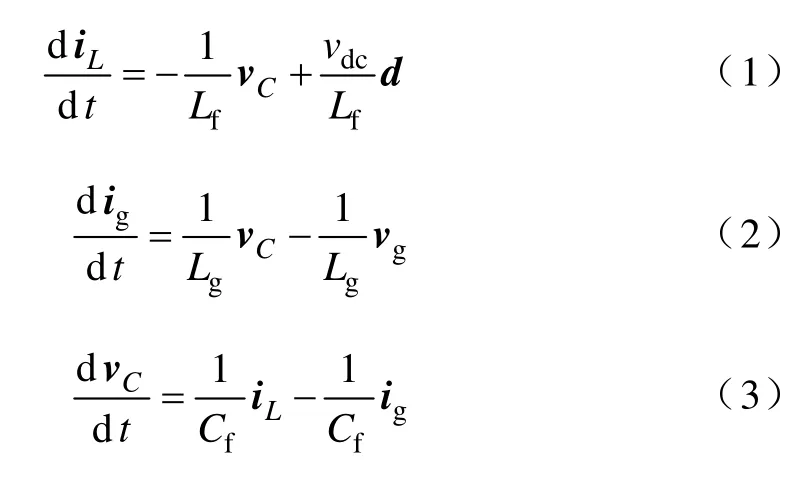
式中，vdc為輸入直流母線電壓值；vg為電網電壓矩陣；d 為占空比矩陣，且

靜止坐標系到旋轉坐標系的轉換矩陣為

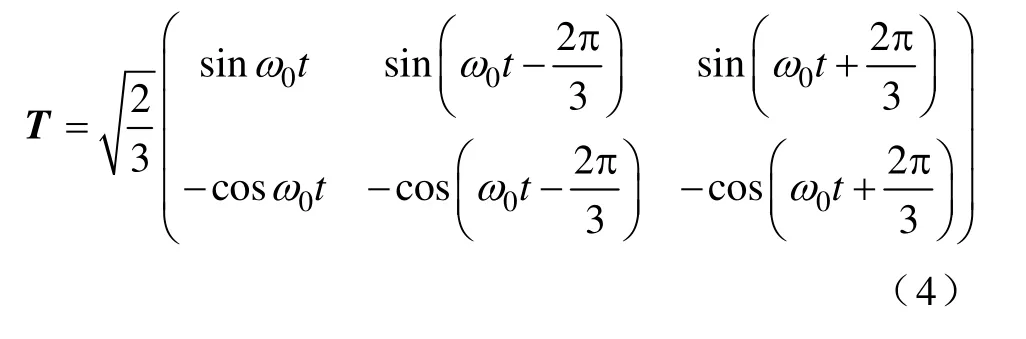
式中，ω0=2πf0，f0是電網的基波頻率。在式（1）、式（2）、式（3）兩端乘上矩陣T，則有

式（5）～式（7）經過拉普拉斯變換后，可以得到占空比dd、dq到輸出電流id、iq的傳遞函數，即并網逆變器的傳遞函數Gp(s)為

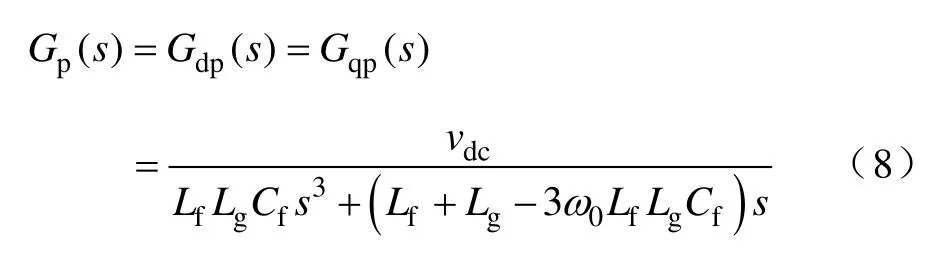
式中，Gdp(s)、Gqp(s)分別為旋轉坐標系下d 軸、q軸的傳遞函數。

同時，從圖1 可以看出，此系統的控制部分主要由以下幾個環節組成:基于改進型重復控制方法的電流控制器，使逆變器注入到電網的電流跟隨電流基準id_ref、iq_ref，并實現低穩態誤差和低THD。鎖相環（Phase Lock Loop，PLL）用來為電流控制器提供采樣頻率與電網頻率的比值 N，以及為abc/dq 轉換提供電網電壓相角θ。當電流基準為零時，逆變器的輸出電壓應該與電網電壓近似同步，以便使電路斷路器可以隨時閉合。電網電壓va、vb、vc轉換為vd、vq后，經過比例環節Kv再加到電流控制器的輸出端，形成電壓前饋，可以實現這個目的。電流id、iq經過比例環節Kcp(其值為2πf0(Lf+Lg)/vdc)后同樣加到電流控制器的輸出端，以實現解耦控制。由于此系統由穩定的直流源供電，因此不需要額外的直流母線電壓控制環節。

3 改進型重復控制方法的原理與設計

重復控制技術的內模如圖2 所示。其中圖2a為時域框圖，圖2b 為離散域框圖，由N 個先進先出（First In First Out，FIFO）單元組成；N=fs/f0=T0/Ts,為采樣頻率fs和電網頻率f0的比值。當電網頻率變化時，比值N 不能保持為一個整數，然而離散域中使用的FIFO 單元只能為整數個，這個差別將使離散域重復控制環節的諧振頻率偏離電網實際的基波與諧波頻率，從而降低了整個系統的性能。

圖2 重復控制技術的內模Fig.2 Internal model of repetitive control technique

圖3 為本文提出的改進型重復控制的離散域框圖。圖中Gp(z)為逆變器傳遞函數，Io(z)為逆變器輸出電流，Iref(z)為電流基準，ID(z)為電流干擾，E(z)為電流跟蹤誤差。重復控制環節包含以下三部分:

（1）重復控制內模1/(1-Q(z)z-Ni):由Q(z)與延時環節z-Ni級聯后再經正反饋后構成。

（2）延時環節z-Nr:傳統重復控制中，Nr=N[14,15]；而在本文中，比值N 隨電網頻率的變化而變化，且不能保持為整數。為了簡化設計，本文最終選取Nr為固定的整數，其值具體為|fs/fr|，fr為電網額定頻率。當電網頻率變化時，固定取值的Nr將偏離實際的比值N，但其僅造成控制系統的相位有少許偏差，而對重復控制的內模沒有影響。

（3）補償環節KczNcGc(z):與傳統重復控制的設計方法相同[14,15]。Kc為重復控制環節的增益；超前環節zNc（Nc為整數）作為相位補償器用來補償逆變器傳遞函數Gp(z)以及濾波器Gc(z)引起的相位滯后，使zNcGc(z)Gp(z)在低頻段近似零相位；濾波器Gc(z)的作用是使Gc(z)Gp(z)在中低頻段保持單位增益，在高頻段增益迅速衰減。

圖3 改進型重復控制的離散域框圖Fig.3 Diagram of the improved repetitive control in discrete-time domain

傳統重復控制中，Q(z)通常選取為一個稍小于1 的常數，或者一個普通低通濾波器；當電網頻率變化時，這兩種選取均會使重復控制的內模特性偏離理想重復控制內模1/(1-z-N)的特性。為了解決這個問題，本文提出了一個基于線性插值法[13]的數字濾波器，用以代替傳統重復控制中的Q(z)。該數字濾波器的傳遞函數為

式中，D 等于比值N 的小數部分，而圖3 中的Ni等于比值N 的整數部分；即Ni=|N|，D=N-Ni。

式（9）的時域形式為

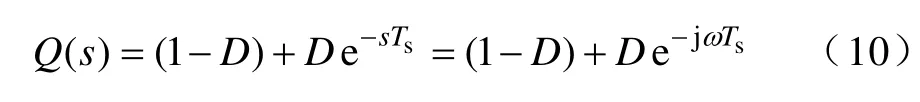
式中，Ts為采樣周期。而由數值D 構成的延時環節z-D的時域形式為

由歐拉公式，式（10）、式（11）可以分別修改為

如果式（12）與式（13）相等，可以推出

在低頻段,考慮到電網基波及其主要諧波頻率相對于采樣頻率fs很小，有

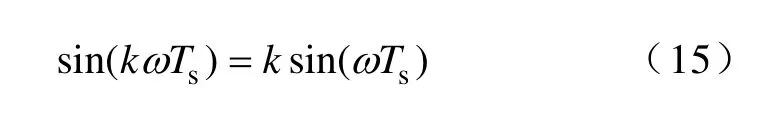
將式（15）代入式（14）,可以證明式（14）成立。則在低頻段，基于式（9）的數字濾波器Q(z)能夠逼近于延時環節z-D。而Q(z)與z-Ni級聯后，能夠使該重復控制的內模逼近于理想重復控制的內模1/(1-z-N)。

本文提出的數字濾波器Q(z)，作為線性插值法的一種實際應用，其形式與文獻[12,16]中所采用的插值法一致。不同之處在于，該Q(z)的系數由比值N 的小數部分D 決定，當比值N 已知時，Q(z)的系數為固定值且計算十分簡捷；同時，Q(z)的作用為逼近于延時環節z-D，其在重復控制環節中的意義直觀、明確。

本文提出的改進型重復控制方法，當電網頻率變化時，根據PLL 提供的采樣頻率fs與當前電網實際頻率f0的比值N，計算出數字濾波器Q(z)的系數以及延時環節z-Ni中Ni的值，從而使此重復控制的諧振頻率與電網實際的基波及諧波頻率相吻合，保持其重復控制環節逼近于理想重復控制，并最終使并網逆變器系統實現良好的穩態跟蹤性能和較低的THD，以及實現對電網頻率變化的適應性。

可以看出，由于Q(z)的系數以及Ni需根據電網頻率f0在線實時計算，因此PLL 的性能對該重復控制方法存在明顯的影響。本文采用了文獻[17]中的方法設計PLL，該方法將電網電壓進行了abc/dq 變換，對變換后的信號進行調節從而實現鎖相功能。為了減小PLL 檢測到的頻率與電網實際頻率之間的誤差，本文PLL 中調節環節（具體為比例積分器）的帶寬，設計得要低于其常規取值范圍[17]。盡管此時PLL 的動態性能會較差，但由于重復控制本身的動態響應極慢，因此對系統的整體性能不存在明顯影響。同時，由于Q(z)系數的計算過程十分簡捷，適合于高頻率的在線實時更新，因此為了簡化控制方法的具體實施，本文中PLL 輸出檢測值的頻率以及Q(z)系數的計算頻率均與系統采樣頻率相同。

圖4 為理想重復控制，文獻[11]提出的重復控制，以及本文提出的改進型重復控制的內模，在540～660Hz 之間的伯德圖。圖中采樣頻率 fs為10kHz，電網實際頻率f0為50.1Hz，則N=199.6，Ni=199，D=0.6。從圖4 中可以看出，文獻[11]提出的采用可變一階低通濾波器的重復控制方法，其諧振頻率在諧波處明顯偏離了理想重復控制，因此其諧波抑制能力與傳統重復控制一樣，均較差；而本文提出的改進型重復控制方法，其特性能夠保持逼近于理想重復控制，尤其是在諧波頻率處，因此具有良好的穩態跟蹤性能和諧波抑制能力。

圖4 不同重復控制的內模伯德圖Fig.4 Bode plots of different repetitive control internal models

4 仿真及實驗結果

本文研究的三相并網逆變器系統的具體參數見下表。

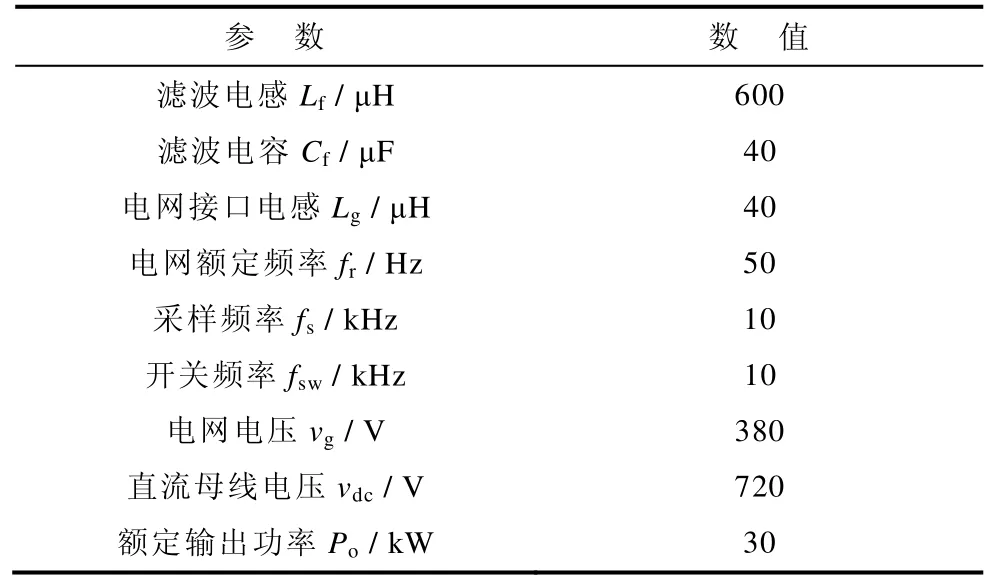
表 逆變器系統的參數Tab. Parameters of the inverter system

系統仿真使用的是Matlab 軟件中的Simulink。系統的額定輸出功率為30kW，則每相輸出電流的額定有效值為45A。

為了驗證本文提出的改進型重復控制方法的有效性，這里也列出了文獻[11]中重復控制方法的仿真結果。圖5 和圖6 分別為電網頻率為50.1Hz、49.9Hz時逆變器A 相輸出電流ia和電流跟蹤誤差eia的仿真結果。當電網頻率為50.1Hz 時，改進型重復控制的逆變器輸出電流THD 為2.54%，而文獻[11]中重復控制的電流THD 為3.45%。當電網頻率為49.9Hz時，電流THD 分別為2.52%和3.81%。從仿真結果可以看出，文獻[11]中重復控制方法的系統性能與當前電網的實際頻率有關，這是因為該重復控制方法的諧振頻率雖然在基波處能夠吻合，但在諧波處仍然有所偏離，且偏離程度隨電網頻率的不同而不同；而本文提出的改進型重復控制方法，其系統的穩態跟蹤性能以及諧波抑制能力基本保持不變，并且要優于文獻[11]中的重復控制方法。

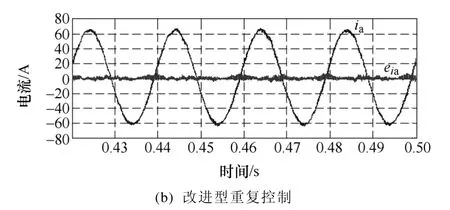
圖5 電網頻率為50.1Hz 時輸出電流ia及電流跟蹤誤差eia的仿真結果Fig.5 Simulation results of output current iaand current tracking error eiaat 50.1Hz grid frequency

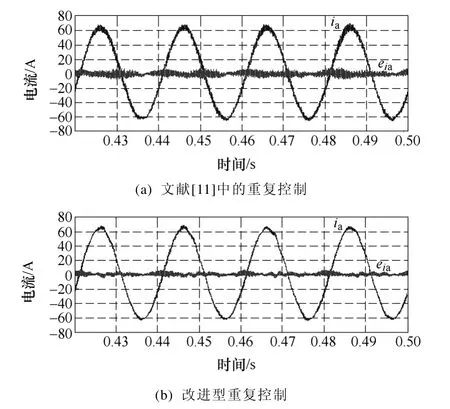
圖6 電網頻率為49.9Hz 時輸出電流ia及電流跟蹤誤差eia的仿真結果Fig.6 Simulation results of output current iaand current tracking error eiaat 49.9Hz grid frequency

本文對基于DSP TMS320F2407 控制的三相并網逆變器樣機進行了實驗驗證。該樣機中三相逆變橋為三菱公司提供的IPM 模塊PM300CAL120。

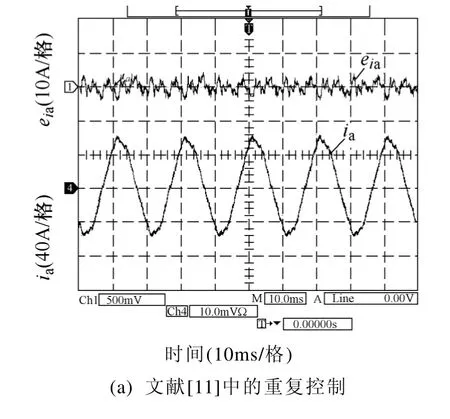
圖7 輸出電流ia及電流跟蹤誤差eia的實驗波形Fig.7 Experimental waveforms of output current iaand current tracking error eia

圖7 給出了文獻[11]中重復控制和改進型重復控制下，逆變器A 相輸出電流ia和電流跟蹤誤差eia的實驗波形。在圖7 中，采用改進型重復控制方法時的電流穩態誤差要低于采用文獻[11]中重復控制方法時的電流誤差，而其輸出電流的波形也相對較優，從而說明本文提出的方法能夠顯著提高系統的穩態跟蹤性能。

圖8 為逆變器輸出電流ia的傅里葉分析結果。可以看出，改進型重復控制方法的電流 THD（2.89%），低于文獻[11]中重復控制方法的電流THD（4.25%），從而驗證了本文提出的方法在抑制并網逆變器輸出電流諧波上的有效性。

圖8 逆變器輸出電流ia的傅里葉分析結果Fig.8 FFT results of inverter output current ia

5 結論

本文提出了一種改進型重復控制方法，它通過采用一個可以根據電網實際頻率進行快速調整的、基于線性插值法的數字濾波器，使該方法的重復控制內模能夠逼近于理想重復控制內模，實現了對電網頻率變化的適應性。在分析了該數字濾波器設計方法和改進型重復控制方法原理的基礎上，進行了系統仿真，并對一臺三相并網逆變器樣機進行了實驗，驗證了該方法對于提高并網逆變器系統的穩態跟蹤性能，降低系統輸出電流的THD，有明顯的作用。由于此方法是對重復控制技術的改進，因此它同樣可以應用于不間斷電源以及有源濾波器等并網系統中。

[1]Francis B A,Wonham W M.The internal model principle for linear multivariable regulators[J].Applied Mathmatics Optimization,1975,2(2):170-194.

[2]Mastromauro R A,Liserre M,Kerekes T,Dell’Aquila A.A single-phase voltage-controlled grid-connected photovoltaic system with power quality conditioner functionality[J].IEEE Transactions on Industrial Electronics,2009,56(11):4436-4444.

[3]Sha D,Wu D,Liao X.Analysis of a hybrid controlled three-phase grid-connected inverter with harmonics compensation in synchronous reference frame[J].IET Power Electronics,2011,4(7):743-751.

[4]Bojoi R I,Limongi L R,Roiu D,et al.Enhanced power quality control strategy for single-phase inverters in distributed generation systems[J].IEEE Transactions on Power Electronics,2011,26(3):798-806.

[5]Delghavi M B,Yazdani A.Islanded-mode control of electronically coupled distributed-resource units under unbalanced and nonlinear load conditions[J].IEEE Transactions on Power Delivery,2011,26(2):661-673.

[6]耿攀,吳衛民,葉銀忠,等.基于重復控制的單相分時復合級聯光伏逆變器控制[J].電工技術學報,2011,26(3):116-122.Geng Pan,Wu Weimin,Ye Yinzhong,et al.Singlephase time-sharing cascaded photovoltaic inverter based on repetitive control[J].Transactions of China Electrotechnical Society,2011,26(3):116-122.

[7]賈要勤,王曉濱,楊強.并聯有源電力濾波器的自適應重復控制[J].電工技術學報,2011,26(10):118-122.Jia Yaoqin,Wang Xiaobin,Yang Qiang.Adaptive repetitive control of parallel active power filter[J].Transactions of China Electrotechnical Society,2011,26(10):118-122.

[8]盧聞州,周克亮,楊云虎.恒壓恒頻 PWM 變換器nk±m 次諧波重復控制策略[J].電工技術學報,2011,26(5):95-100.Lu Wenzhou,Zhou Keliang,Yang Yunhu.nk±m order harmonic repetitive controller for CVCF PWM converters[J].Transactions of China Electrotechnical Society,2011,26(5):95-100.

[9]于晶榮,粟梅,孫堯.有源電力濾波器的改進重復控制及其優化設計[J].電工技術學報,2012,27(2):235-242.Yu Jingrong,Su Mei,Sun Yao.Improved repetitive control and its optimization for active power filter[J].Transactions of China Electrotechnical Society,2012,27(2):235-242.

[10]Hornik T,Zhong Q C.H∞repetitive voltage control of grid-connected inverters with a frequency adaptive mechanism[J].IET Power Electronics,2010,3(6):925-935.

[11]Hornik T,Zhong Q C.A current-control strategy for voltage-source inverter in microgrids based on H∞and repetitive control[J].IEEE Transactions on Power Electronics,2011,26(3):943-952.

[12]Cao Zhenwei,Ledwich G F.Adaptive repetitive control to track variable periodic signals with fixed sampling rate[J].IEEE/ASME Transactions on Mechatronics,2002,7(3):378-384.

[13]Williams A B,Taylor F J.Electronic filter design handbook[M].Chicago:McGraw-Hill Professional,2006.

[14]Yang Shuitao,Cui Bin,Zhang Fan,et al.Arobust repetitive control strategy for CVCF inverter with very low harmonic distortion[C].IEEE Applied Power Electronics Conference,2007:1673-1677.

[15]Shi Xiaojie,Shen Yuwen,Wang Zhiqiang,et al.A repetitive-based controller for a hybrid filter with high quality grid current waveform[C].IEEE Applied Power Electronics Conference,2011:757-762.

[16]Wang Yigang,Wang Danwei,Zhang Bin,et al.Fractional delay based repetitive control with application to PWM DC/AC converters[C].IEEE Control Applications,2007:928-933.

[17]Chung Se-Kyo.A phase tracking system for three phase utility interface inverters[J].IEEE Transactions on Power Electronics,2000,15(3):431-438.