混雜系統理論及其在三相逆變電路開路故障診斷中的應用

李 寧 李穎暉 朱喜華 雷洪利 俞 佳

（1.空軍工程大學航空航天工程學院 西安 710038 2.西安富士達科技股份有限公司 西安 710077）

1 引言

電力電子電路在工業、軍事、航空航天等重要領域已得到廣泛的應用，并對系統的可靠性有著重要的影響。因而，研究電力電子電路通用的、可靠的故障診斷方法用于準確監測電路的運行狀態具有重要意義[1,2]。

電力電子電路傳統開關函數模型只考慮了電路的控制變遷，而忽略了與電路連續狀態相關的條件變遷，可能導致重要故障信息的丟失，從而影響故障診斷的實時性[3]，由于電力電子電路是一種典型的混雜系統，因而混雜系統理論為電力電子電路的故障診斷提供了新的思路。

混合邏輯動態建模作為混雜系統建模方法中的一種，是將系統整個當作一個微分方程組來處理，離散事件以條件的方式嵌入微分方程組中，可以兼顧電路的控制變遷和條件變遷[4,5]。文章建立了電力電子電路的混合邏輯動態模型，在此基礎之上，研究電路的故障診斷方法。

利用事件辨識進行故障診斷是電力電子電路的一種新的基于混雜系統理論的故障診斷方法，其原理是：實時檢測電路事件變遷序列，并與期望序列進行比較，從而實現電路故障的診斷[1]。此方法用于Buck 電路時，由于Buck 電路只有4 個離散事件，診斷效果良好，但當電路離散事件較多時，比如三相逆變電路有212個離散事件，就難以實現，主要存在以下幾個問題：

（1）實際變遷序列的檢測：開關頻率較高導致離散事件變遷迅速，檢測模塊難以跟蹤實際電路的變遷。

（2）期望變遷序列的獲取：不同控制策略的期望變遷序列不同，影響算法的通用性。

（3）觀測器的數量：對所有離散事件進行觀測，需要的觀測器數量龐大。

針對以上問題，由于電路故障事件集是離散事件集的一個子集，文章以電路故障事件集的辨識代替電路離散事件集的辨識，提出基于故障事件識別向量的電力電子電路故障診斷方法，具有通用、易于實現、診斷效果好等特點。

2 電力電子電路的混合邏輯動態模型

混雜系統是指由連續變量動態系統和離散事件動態系統相互混雜、相互作用的系統[6,7]。電力電子電路中開關器件通斷的每一種組合均是一個離散事件，該階段中電路變量的變化受狀態方程的約束，具有連續變量的性質，因此電力電子電路是一種典型的混雜系統，可以利用混雜系統理論和方法解決電力電子電路的問題[8]。

混合邏輯動態建模作為混雜系統建模方法中的一種，是將系統整個當作一個微分方程組來處理，離散事件以條件的方式嵌入微分方程組中，同時兼顧了電路的控制變遷和條件變遷。根據電力電子電路的運行規律，可以建立電力電子電路的混合邏輯動態模型

式中，x=(xc,xl)T為狀態變量，其中連續狀態xc∈Rnc，離散狀態xl∈(0,1)n1，n=nc+nl；輸出變量y=(yc,yl)T，其中連續輸出yc∈Rpc，離散輸出yl∈(0,1)p1，p=pc+pl；輸入變量u=(uc,ul)T，連續輸入uc∈Rmc，離散輸入ul∈(0,1)m1；σ和z分別代表系統輔助邏輯變量和輔助連續變量；A、B1～B3、C、D1～D3、E1～E5為系數矩陣。

3 電力電子電路故障診斷的基本機理

開關器件狀態的每次變化均可導致電路由初始離散事件變遷至目標離散事件，形成電路的一次變遷，可將電路的變遷分為控制變遷和條件變遷兩類[3,9,10]。

定義1：由開關管控制信號引起的電力電子電路拓撲變化稱為控制變遷。

定義2：由電路自身狀態變化導致不控器件通、斷狀態改變而引起的電力電子電路拓撲變化稱為條件變遷。

控制器信號、電路自身狀態、開關器件故障等都可引起電路開關狀態的變化[11]，其中將由開關器件故障導致的電路變遷稱為故障變遷，故障變遷對應的目標離散事件的集合定義為故障事件集，故障事件集中的元素稱為故障事件，可見電路故障事件集就是電路離散事件集的一個子集。

定義3：假如有最簡狀態向量X=(X1···Xi···Xn)在電力電子電路所有故障事件中具有不同的變化規律，則稱向量X=(X1···Xi···Xn)為電路的故障事件識別向量。

以電路混合邏輯動態模型為基礎，分別建立電路每個故障事件的故障模型，基于第j個故障事件的故障模型構造電路觀測器，觀測器估計值為X?j，與實際工作電路的故障事件識別向量Xi進行比較，得到第j個故障事件的故障模型觀測器殘差Zj，其中Xi為故障事件識別向量X=(X1···Xi···Xn)的第i個分量。

定義殘差向量：Z=(Z1···Z j···Zm)，其分量表達式如式（2），其中Z的維數m等于故障事件數，且m＞n，n為故障事件識別向量X的維數；q∈Q，Q是電力電子電路的故障事件集；hj為一大于零的常數，稱為故障辨識閾值，則有

即，電路第j個故障事件的故障模型的觀測器殘差Zj小于故障辨識閾值時，認為電路出現了第j個故障事件對應的故障。

準確的故障辨識閾值hj對于電路故障的診斷具有重要意義，影響故障辨識閾值的因素有：電路故障模型的準確性、選取的故障事件識別向量及各種干擾等。

故障辨識閾值hj的存在性：發生故障后，如果電路的運行仍滿足基爾霍夫定律，則可建立電路該故障事件的數學模型，即故障模型，通過故障模型觀測器的估計值與實際電路值的比較，得到殘差Zj，那么必然存在一個閾值hj，當電路再次發生同樣故障時，使

故障辨識閾值hj的設置原則：假設電路的故障事件集為{A1…Aj…Am}，建立故障事件的故障模型。當電路依次發生故障事件A1…Aj-1、Aj+1…Am時，故障事件Aj的故障模型觀測器的估計值與電路實際值進行比較得到殘差集合為{B1…Bj…Bm-1}，則故障事件Aj對應的故障辨識閾值hj滿足

故障事件辨識規則：實時檢測殘差向量Z，對于分量滿足式（3）的觀測器殘差所對應的故障事件集中的元素就是電路實際發生的故障。

由上述故障事件辨識規則可以推導出，電力電子電路故障診斷的基本步驟如圖1 所示，首先，根據電路故障模式，確定電路的故障事件集；其次，以故障事件集為基礎，確定電路的故障識別向量及及故障事件的故障模型；最后根據故障模型觀測器的殘差向量得出診斷結果。

圖1 故障診斷流程圖Fig.1 Flow chart of fault diagnosis process

4 逆變電路故障診斷

4.1 電路混合邏輯動態模型

逆變電路主拓撲如圖2 所示，下面依次建立逆變電路的混合邏輯動態模型、確定電路故障事件集和故障事件識別向量、得出電路的故障模型。

圖2 三相逆變電路Fig.2 Three-phrase inverter diagram

開關管Sa1～Sa6的開關信號為s1～s6，“1”表示導通，“0”表示關斷，對于逆變器a 臂(b、c 兩臂類似)，定義電流ia流入濾波電感的方向為正。引入邏輯運算符，“∨”表示析取、“∧”表示合取、“～”表示取非、“?”表示等價，將離散事件ia＞0和ia＜0 分別用邏輯變量σa=1和σa=0 表示，有

對于三相逆變電路，根據其工作原理有如下邏輯關系式：

由上述邏輯關系得到電壓uao的數學描述為

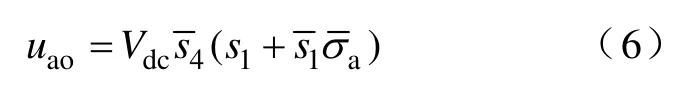
假定電路濾波電阻均為r，電感為L，負載電阻為R，得到逆變電路的混合邏輯動態向量模型為

其中

uA、uB、uC分別為三相輸出電壓。

4.2 電路故障事件辨識

對于電路a 臂，故障事件集=｛Sa1開路故障，Sa4開路故障，Sa1和Sa4同時開路故障｝，下面針對故障事件分別建立其故障模型。

當Sa1開路故障時[12]，相當于Sa1控制信號s1=0，將其代入式（7）得Sa1開路故障的故障模型輸入

同理可得Sa4開路故障、Sa1和Sa4同時開路故障時，電路故障模型的輸入分別為

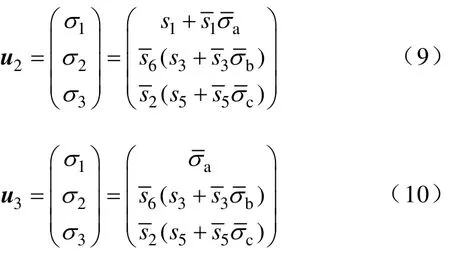
將式（8）～式（10）分別代入式（7）即可得到電路故障事件集的故障模型，可以看出，對于三相逆變電路a 臂的故障事件集，故障事件不同時，ia具有不同的變化規律，因而可以選擇X=(iaibic)作為三相逆變電路的故障事件識別向量。

如圖3 所示，基于故障事件識別向量和電路故障事件集的故障模型構建電路狀態觀測器，得到殘差向量，通過故障事件辨識規則的判斷即可完成對實際電路故障事件的辨識。

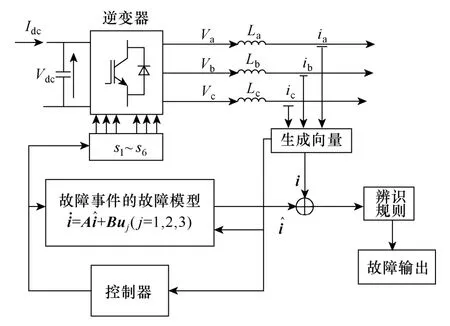
圖3 逆變電路故障診斷Fig.3 Inverter diagnosis diagram

5 仿真與實驗驗證

如圖 2 所示逆變電路拓撲，仿真參數如下：udc=270V，濾波電感L=100μH，濾波電阻R=25mΩ，額定頻率為400Hz。仿真結果如圖4 所示，以a 臂故障為例，故障時間為 0.01s，故障事件集=｛Sa1開路故障，Sa4開路故障，Sa1和Sa4同時開路故障｝，為便于后文敘述，將故障事件集簡記為：故障事件集=｛事件1，事件2，事件3｝，根據上述三種故障事件的故障模型如式（8）和式（9）及圖3 逆變電路的故障診斷原理，將電路故障模型的估計值與實際電路工作值進行比較，得到電路的殘差 (即電路故障事件的故障模型觀測器殘差，如式（2）所示)，將三種故障事件對應的殘差記為｛殘差1、殘差2、殘差3｝。如式（3）所示，若要可靠地完成故障診斷，需要給三種故障事件的故障模型觀測器殘差設定準確的辨識閾值，通過分析及仿真實驗，取h1=h2=h3=0.2。圖4a～圖4d 分別為Sa1開路故障、Sa4開路故障、Sa1和Sa4同時開路故障時，殘差1、殘差2和殘差3 的仿真結果，從圖4 可以看出，當Sa1開路故障時，殘差1、3 滿足辨識規則，當Sa4開路故障時，殘差2、3 滿足，當Sa1和Sa4同時開路故障時，僅有殘差3 滿足，因此根據辨識結果可以確定電路的故障事件，從而診斷出發生故障的類型。

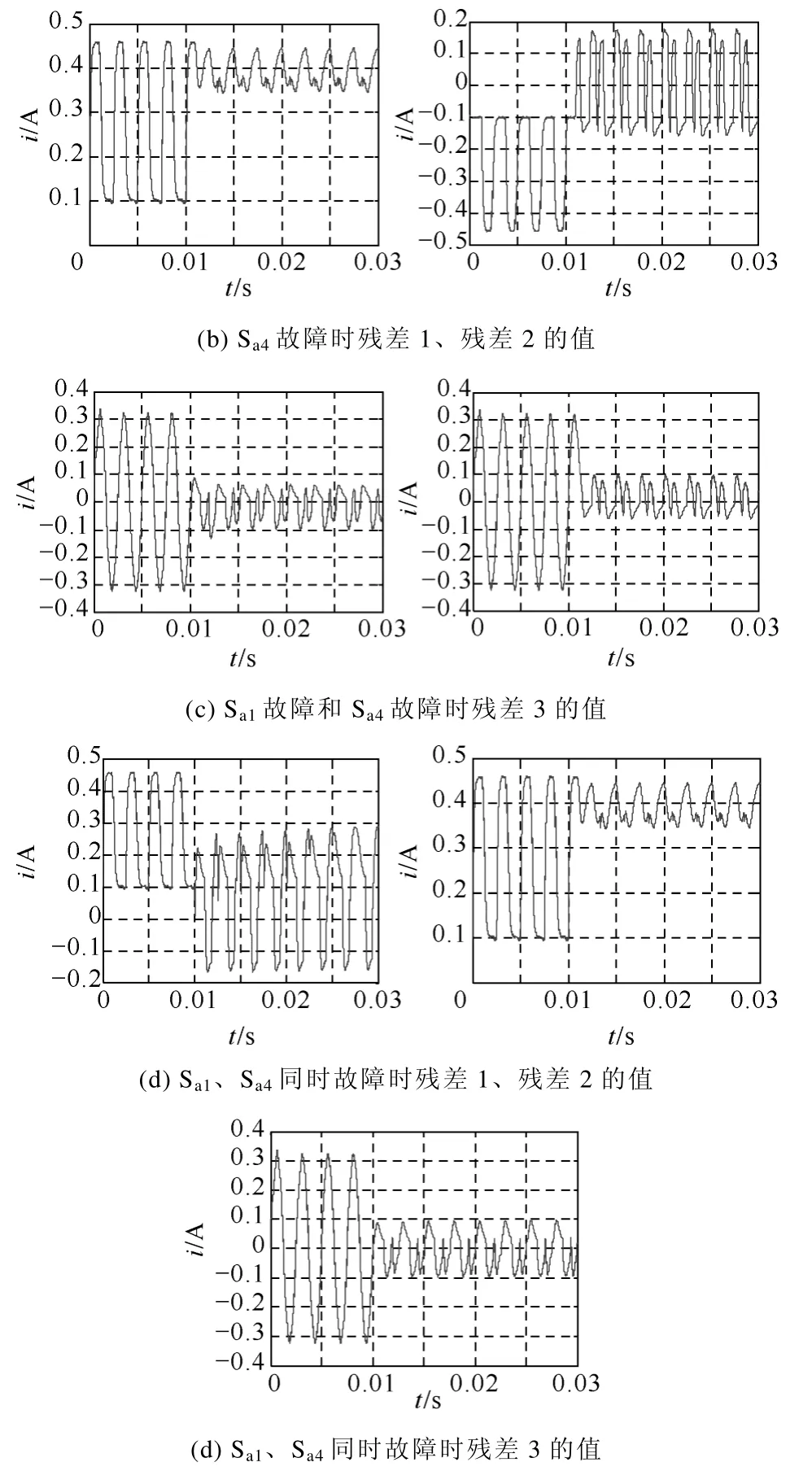
圖4 仿真結果Fig.4 Simulation results

實驗平臺基于TMS320F2407和EPIC6Q240。三相電流檢測電路由電流傳感器、偏置電路和限幅電路組成。濾波電感、電阻分別為：100μH、25mΩ，直流電壓為270V，設定閾值h=2.5。實驗結果如圖5 所示，圖5a 為Sa1開路故障時，事件1 的故障模型觀測器的輸出殘差，圖5b 為Sa4開路故障時，事件2 的故障模型觀測器的輸出殘差；圖5c 為Sa1和Sa4同時開路故障時，事件3 的故障模型觀測器的輸出殘差，均能滿足辨識規則，診斷故障事件。

圖5 實驗結果Fig.5 Test results

6 結論

本文分析并建立了電力電子電路混合邏輯動態模型，克服了電力電子電路傳統開關函數模型只描述電路的控制變遷而忽略電路的條件變遷這一問題，使電路的數學模型更為準確，有利于電路故障診斷的研究。在電路混合邏輯動態模型的基礎上，基于故障事件識別向量，研究了電力電子電路故障診斷方法，該方法適用于多離散事件電路，以逆變電路故障診斷的仿真和實驗驗證了所提方法的可行性和有效性，為電力電子電路的故障診斷提供了一種新的思路和方法。

[1]張志學,馬皓,毛興云.基于混雜系統模型和事件辨識的電力電子電路故障診斷[J].中國電機工程學報,2005,25(3):49-53.Zhang Zhixue,Ma Hao,Mao Xingyun.Fault diagnosis for power electronic circuits based on hybrid system theory and event identification[J].Proceedings of the CSEE,2005,25(3):49-53.

[2]張志學.基于混雜系統理論的電力電子電路故障診斷[D].杭州:浙江大學,2005.

[3]安群濤.三相電機驅動系統中逆變器故障診斷與容錯控制策略研究[D].杭州:浙江大學,2011.

[4]李瓊林,劉會金,宋曉凱.基于切換系統理論的三相變流器建模及其穩定性分析[J].電工技術學報,2009,24(11):89-96.Li Qionglin,Liu Huijin,Song Xiaokai.Modeling and stability analysis of three-phase converter based on switching system theory[J].Transactions of China Electrotechnical Society,2009,24(11):89-96.

[5]Sreekumar C,Vivek Agarwal.A hybrid control algorithm for voltage regulation in DC-DC boost converter[J].IEEE Transactions on Industrial Electronics,2008,55(6):2530-2538.

[6]李雄杰,周東華.基于混雜模型和濾波器的電力電子電路故障診斷[J].西北大學學報,2011,41(3):410-414.Li Xingjian,Zhou Donghua.Fault diagnosis based on hybrid system model and filter for power electronic circuits[J].Journal of Northwest University,2011,41(3):410-414.

[7]Du Jingling,Song Chunyue,Li Ping.Modeling and control of a continuous stirred tank reactor based on a mixed logical dynamical model[J].Chinese Journal Chemical Engineering,2007,15(4):533-538.

[8]Jean Buisson,Pierre Yves Richard,Herve Cormerais.On the stabilisation of switching electrical power converters[C].Proceedings of 8th International Workshop on Hybrid Systems:Computation and Control,vol.3414 of Lecture Notes in Computer Science.Zurich,Switzerland:Springer,2005.

[9]Vichare N M,Pecht M G.Prognostics and health management of electronics[J].IEEE Transactions on Components and Packaging Technologies,2006,29(1):222-229.

[10]Bemporad A,Mignone D,Morari M.Moving horizon estimation for hybrid systems and fault detection[C].In Proceedings of ACC’99,San Diego,CA,USA,1999:2471-2475.

[11]Yu Zhang,Li Peng,Shanxu Duan.The dynamic model of three-phase inverters with magnetic couples[C].The 33rd Annual Conference of the IEEE Industrial Electronics Society,2007.

[12]Hans Brink Hansen,Jan Dimon Bendtsen.A hybrid model of a brushless DC motor[C].IEEE Multi-Conference on Systems and Control,Singapore,2007.