高等數學教學中創新思維的研究與實踐

王 霞

（天津科技大學，天津 300222）

多年的教學實踐我們發現，許多學生不會數學思維，學習數學只會死記硬背，表現在期末考試只要不出作業原題，不論考試題多么簡單，就會出現預想不到的大面積不及格現象，如何在教學的過程中培養學生的數學思維能力，尤其是數學創新思維能力，是擺在我們一線教師面前一項緊迫任務。

一、數學創新思維的含義與特征

思維是人腦對外界事物間接、概括的反映，它反映的是事物的本質和內部規律。

創新思維是思維活動中最高層次的思維，它是主動地、創造性地發現新事物、提出新見解、解決新問題的思維形式。比如常說的“舉一反三”、“觸類旁通”等都屬于創新型思維，即在學習中不因循守舊、善于獨立思考與分析、能夠積極主動探索新問題的一種思維方式。

數學思維是以數及形為思維對象，以數學語言為載體，以認識和發展數學規律為目的的一種思維活動。它是一般思維的特殊形式，主要包括抽象思維、形象思維、逆向思維，發散思維和直覺思維。即數學思維主要表現在意識力求抽象概括化、對象力求形式化、背景力求直觀形象化、過程力求邏輯化、結果力求應用化。

數學創新思維是數學思維與創新思維相結合的產物，它是在已有的數學知識經驗基礎上產生新的思維結果，其特征表現在敢于探索，能夠擺脫思維的常規束縛，產生新穎的、前所未有的思維成果。

二、高等數學內容蘊含豐富的數學創新思維

數學研究對象是思維的產物，它可以看成是一門思維的科學。數學本身又是一個邏輯體系，是由概念、性質、公式、法則，定理構成。以高等數學為例，其每一個概念都蘊含著逆向思維，即每一個概念都有其反面，如函數有界與無界、連續與間斷、收斂與發散，在解決具體問題時，常用反證法來解決，或用逆否命題，如證明空集是任意集合的子集。逆向思維有利于克服思維定勢的保守性，可尋求新的思路與方法，是一種創造性的思維。

類比思維在高等數學中處處可見，如二元及以上函數、極限、連續、可微的定義都類比一元函數得到；二、三重積分、第一型曲線、曲面的概念、性質都可由定積分的概念、性質類比得到。在解決從一元到多元，從一維到多維，從有限到無限，從離散到連續的問題時，類比的思維方法是非常有效的。

類比是特殊到特殊的思維方式，是根據兩個或兩類所考察的對象之間在某些方面有相同或相似的屬性，并且其中一個對象還有另外的某種屬性，從而推出另一對象也具有相同或相似的該種屬性的思維。由于類比思維是提出新問題和做出新發現的一個重要源泉，也是探索解題思路的重要途徑，故類比思維是創新思維的形式之一。

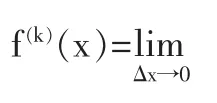
對多元函數求偏導時，將其中一個變量看成未知，其余所有變量均視為已知，即轉化為一元函數求導。在對不定積分與定積分計算時，常用換元法，就是將要求的積分轉化為可以用基本公式來計算的基本情形；二、三重積分的計算的思維方法是分別轉化為兩個、三個定積分來計算，微分方程部分也處處體現了轉化的思維。

轉化思維是通過某種變換過程將復雜的或困難的問題劃歸為與原問題等價的問題，而后者相對與前者較為簡單或比較容易求解，轉化的過程就是創新的過程，即轉化思維是創新思維。

高等數學知識本身的應用就是創新思維，如用夾逼準則方法求數列的極限時，構造不等式的過程就是創新思維過程，還有正項級數的比較判別法，在找另一個正項級數的過程也是創新思維過程，再有設輔助函數、變量代換等，都是創新思維的具體體現。

三、數學創新思維教學實踐

數學創新思維能力的培養一定要貫穿整個教學活動中，問題意識是思維的起點，是獨立思考的標志，是創新的開始。學生的問題意識越強烈，學習過程中不斷地產生“為什么？ ”、“是什么？ ”、“怎么辦？ ”、“怎么變？ ”等，其思維也就越主動、越積極、越自覺，也就越有利于問題發現、問題發展和問題解決，反過來又能有力地促進學生數學思維能力的提高和創新意識的形成和發展。

如在講導數概念時，讓學生明確在均勻情況下凡是用除法定義的概念（物理量），在不均勻的情況下絕大多數都用導數來描述，還有生物種群的生長率和死亡率、放射性物質的衰變率、冷卻過程的溫度的變化率等必須用導數來度量，這就回答了為什么要學導數的概念。

導數是什么？從數學的角度，它就是個數，是函數的改變量與自變量改變量之比的極限值，是函數值隨自變量變化快慢程度的一個度量；從物理角度，它是函數在一點的變化率；從幾何角度，它是曲線過一點的切線的斜率；經濟上，它表示邊際。

導數存在的條件是什么？如果導數存在，如何求導數，即具體的求導方法？由于高等數學的主要研究對象是初等函數，由初等函數的結構自然得到下面的求導線索，如圖1所示。

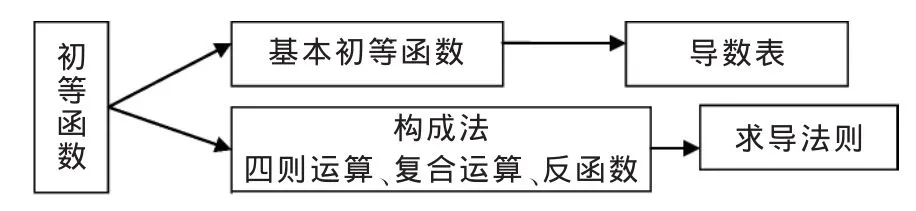
圖1 求導線索圖

導數有什么用？即在一個區間上可導的函數會有什么性質？這就是微分中值定理一章回答的問題。

在講微積分基本定理這一節時，首先，讓學生明白的基本問題是：什么樣的函數可積分？怎樣求可積函數的定積分？將定積分的概念類比導數的定義，可知：在均勻情況下用乘法定義的（物理）量，在不均勻的情況下一般都是用定積分，即導數與積分有互逆的關系。

學習數學，離不開數學思維，可以說數學的本質特性就是思維。我們經歷了數學概念的引入，定理的發現，規律的探求等諸多過程。在這些認識活動過程中，是促使學生能夠一步一步向前走，又能夠使學生的智慧逐步提升，變得越來越聰明。即數學思維和數學思維方法，是數學學習過程中必須接觸的內容，學生在學習高等數學的過程中，能力的提高主要在于對數學思維方法的掌握。

[1]王茹.國內數學創新思維能力研究述評[J].牡丹江教育學院學報，2008（4）.

[2]陳定元.高等教育中數學創造性思維的培養[J].安慶師范學院學報，2009（2）.

[3]楊錦偉，黃堃.基于高等數學創新思維的創新人才培養[J].教育與職業，2013（26）.

[4]聶東明.培養學生數學創新思維的教學策略[J].衡陽師范學院學報，2003（3）.

[5]趙世安.數學創新思維的心理機制及其能力的培養[J].廣西民族學院學報，2001（2）.

[6]張文強.談數學創新教育[J].錦州范學院學報，2002（2）.