短波通信信道衰落技術的研究與仿真
秦小軍,肖 強
(陜西烽火電子股份有限公司,陜西 寶雞 721006)
1 試驗組織及參數設置
本試驗的重要目的就是分析不同傳播模式信號的衰弱情況,從中提取出各傳播模式信號幅度伴隨時間的變化信息。試驗運用定頻探測以及掃頻探測結合的模式。系統工作周期是30min,每周期開始時進行一次掃頻,再于定頻點持續進行16次探測,時間間隔是1min,定頻探測自整分點開始,共計發射512個信號,時間為25.6s。試驗用發射機功率為400W,采樣頻率是160kHz,線性調頻脈沖信號帶寬是40kHZ,脈沖重復周期是50ms。
2 分析試驗數據
所選電路及10MHz頻點上基于頻域信號最大原則提取規則E模式、Es模式以及具有大小不均體的F2低角模式信號幅度隨時間變化的示意圖(見圖一)。圖像顯示25.6s觀察時間內E模式信號伴隨著時間變化幅度改變很小,具體變化可以大致使用線性函數來展開敘述,圖中虛線所示為直線擬合結果。Es模式以及含有大小不均勻體的F2模式信號幅度變化明顯,在25.6s內進行了多次深度快衰落。
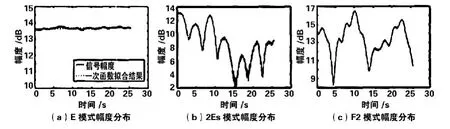
圖一 11時15分各模式信號幅度分布示意圖
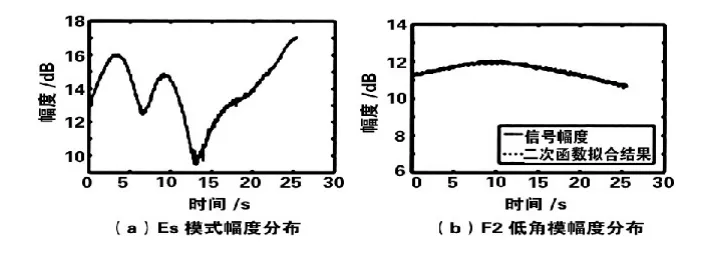
圖二 14時47分各模式信號的幅度分布示意圖
對比圖一、二,結果顯示同一電離層下,若傳播模式不相同,信號幅度的變化趨勢就不同。但同種傳播模式,在不同的電離層下,信號幅度變化趨勢的差異性就很大。
電離層是線性時變通道,通過電離層傳播以后的電波信號的變化具有隨機性,需借助統計手段來分析、研究。信號幅度衰落累積分布往往用于信號衰落統計特性。經資料證實、理論計算,在短波信道內可用Rician分布與Rayleigh分布來表示信號幅度衰落分布。
按照上述分析,我們能夠得出這樣的結論:其一,和Rayleigh分布比較,E層和F2層信號幅度衰落分布較為接近Rayleigh分布,而在25.6s內,其幅度變化規則。需重點考慮電離層在短時效應時,需要運用拋物線函數以及線性函數進行大致描述,重點描述出E模式信號以及F2信號幅度隨時間的改變特點。其二,在高于75%置信度時,Es層信號幅度分布概率和Rician分布接近,但和Rayleigh分布較大。
3 關于信道的建模及其仿真
3.1 關于信道的建模
從當前來看,較為齊全的短波信道模型便是Vogler,通常是從功率延遲分布、多普勒頻移以及多普勒展寬三方面來開展信道統計性建模。然而它有以下缺陷:第一,利用平面分層等效關系計算電離層路徑的參數過于簡單。第二,該模型依舊運用復高斯隨機過程模擬信道衰落,過程中的假設不具有普遍意義。
在Vogler模型基礎上,結合電離層斜向探測結果針對短波信道進行建模,各傳播模式信號運用不同幅度衰落描述。考慮到便捷性因素,文中建立的Vogler信道模型是廣義的。其中,相位函數以及時延功率剖面因子仍用Vogler模型形式,隨機調制函數則根據不同電離層及傳播模式而定。
3.2 關于信道的仿真
當短波時,變信道仿真的關鍵是隨機調制函數生成,通常情況下Rayleigh衰落過程實現是由兩路獨立高斯白噪聲各自經多普勒成型濾波器之后作傅立葉反變換得到。但由于短波信道多普勒展寬范圍極小,若直接將高斯白噪聲頻譜與多普勒濾波器傳輸函數相乘,必會引起頻率分辨率過低,我們應用史密斯成形濾波法。
任意選擇探測結果檢驗廣義Vogler模型的精準度。先由實測數據提取各模式信號多普勒信息和時延信息(見表一)。
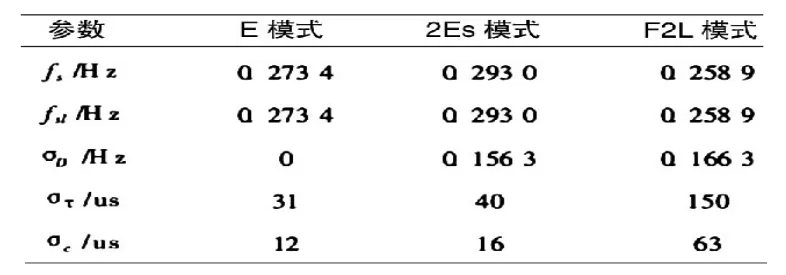
表1 各模式信號的多普勒信息和時延信息

圖三 模型輸出散射函數和實測散射函數的對比
把多普勒信息和時延信息代到信道模型,得到圖三(a)所示的散射函數,圖三(b)則給出了此時實測散射函數圖。
通過兩圖對比我們發現,模型輸出散射函數和實測結果有著相似之處,二者之間最主要的區別是實測散射函數時延功率剖面在低角模在距離處峰值顯著分裂,起伏嚴重,但模型輸出散射函數時延功率剖面則是光滑曲線。這說明模型用時延功率剖面不精確,應進行深入試驗和理論研究。另外,模型輸出未經過一定的抑制手段,因此受到的影響極大。
[1] 凡俊梅,吳振森,焦培南,等.電離層不同傳播模式信號衰落的實驗研究[J].武漢科學學報,2009,(08):13-14.
[2] 張云飛,胡中豫,張宏珉.基于短波接入網的圖像傳輸系統設計與實現[J].四川兵工學報,2009,(10):68-69.

