向量評估遺傳算法優化聚乳酸載藥微球工藝Δ

王婷，馮瑞梅，戴帥，仇麗霞（山西醫科大學衛生統計教研室，太原030001）

在藥物最優制備條件的多目標優化問題中，傳統方法是將多目標問題轉化為一個或一系列的單目標優化問題來解決，這樣存在極大的主觀性。通過這種方式得到的優化解，往往在某一個目標上是最優的，而在另一個目標上可能是較差的，不能保證所有目標都存在最優解，在實際應用中存在不合理的現象。實際上多目標的優化解不是唯一的，是將各個子目標進行協調權衡和折中處理，使各個子目標函數盡可能達到最優，是一組可供選擇的、非受控的解方案集，稱為Pareto非劣解集[1]。

向量評估遺傳算法[2-5]（Vector evaluated genetic algorithm，VEGA）在解決均勻設計試驗的多目標優化問題中，提供合理的Pareto非劣解集。VEGA是1985年由Schaffer提出的，其開創了多目標優化遺傳算法的先河，利用內在并行的方式給出了多目標優化問題的Pareto非劣解集，解決了多目標優化的難題[5]。

聚乳酸（Polylactic acid or polylactide，PLA）的主要原料為速生資源玉米，經發酵制得乳酸，再以乳酸為主要原料而得到聚合物。其在人體內最終代謝為二氧化碳和水，是經美國FDA批準可用于人體的生物降解材料[6]。載藥微球（Microspheres）是一種新型給藥體系，粒徑一般較小（1～250μm），其以高分子材料為載體，制成包裹藥物的球形或類球形微粒，可以被細胞融合或被網狀內皮系統內吞或被溶酶體中的酶降解后釋放出藥物[7]。聚乳酸載藥微球具有良好的生物相容性、生物降解性、靶向性和控釋性，在藥學領域有著廣闊的發展前景。本文將對聚乳酸載藥微球的制備工藝用VEGA進行多目標優化，進而與原文獻比較優化結果。前期本課題組已對VEGA進行了效果評價及程序測試，結果可靠，可用于實際問題的分析，為決策者提供選擇的空間，達到節省人力、物力，降低研究成本的目的。

1 材料

1.1 儀器

UV2300紫外-可見分光光度計（上海天美科技有限公司）；IKA R20.DM型機械攪拌機（廣州儀科設備有限公司）；KQ2200-E型超聲分散機（江蘇昆山市超聲儀器有限公司）；LA-920激光粒度分析儀（日本Horiba公司）。

1.2 藥品與試劑

線形聚d，l-乳酸（華南農業大學合成，相對分子質量：1.2×104）；二氯甲烷（廣州化學試劑廠，分析純）；亮藍（英國Kris公司，分析純）；PVA-224聚乙烯醇（日本Nopco公司，相對分子質量：6000，水解度：95%）。

2 方法與結果

2.1 兩目標（藥物包封率與平均粒徑）的測定

聚乳酸載藥微球用線形聚d，l-乳酸、二氯甲烷、聚乙烯醇等試劑合成，并通過一系列精密儀器測定其含量。以0.4%二氯甲烷的乙醇溶液為空白樣，通過繪制標準曲線得出亮藍的質量濃度（c）在1.0、1.5、2.0、5.0、7.5、10.0 μg/ml范圍內與吸光度（A）的線性關系良好，相關系數達到0.9999。影響工藝制備的因素有內水相體積、二氯甲烷質量濃度、聚乙烯醇質量濃度、攪拌速度及氯化鈉質量分數，評價工藝的指標有藥物包封率（y1，%）和產物平均粒徑（y2，μm）。進而確定目標值藥物包封率與平均粒徑的測定方法，按照以下公式進行計算。

載藥量＝（微球中亮藍的質量/微球的質量）×100%

包封率＝（微球中亮藍的質量/所投亮藍的質量）×100%

取適量的聚乳酸載藥微球，用少量的注射用水分散后，用激光粒度分析儀即可測定載藥微球的平均粒徑。

2.2 試驗設計及模型擬合

2.2.1 均勻設計試驗。采用復乳法制備聚乳酸載藥微球，影響工藝的因素有5個，即內水相體積（x1）、二氯甲烷質量濃度（x2）、聚乙烯醇質量濃度（x3）、攪拌速度（x4）及氯化鈉質量分數（x5），每個因素各有8個水平，按均勻設計試驗U8（85）進行8次試驗，評價工藝的指標有包封率和平均粒徑，試驗結果見表1[8]。

表1 復乳法制備聚乳酸載藥微球均勻設計試驗U8（85）結果Tab 1Results of uniform design U8（85）of Polylactic acid-loaded microspheres prepared by W/O/W emulsion

由表1可見，2號方案包封率最大，6號方案平均粒徑最小，兩個最優目標不在同一個方案中，于是將8次試驗結果根據建立的二次回歸模型中一次項、二次項的符號，得出最優制備工藝為較高的二氯甲烷質量濃度、較高的攪拌速度及較低的氯化鈉質量分數，但并未給出具體解集。

2.2.2 模型擬合。文獻數據采用逐步回歸方法篩選變量，并對兩目標（包封率與平均粒徑）分別建立了二次型回歸模型[8]。以包封率和平均粒徑作為評價指標，得到與x2、x4、x5的回歸模型。

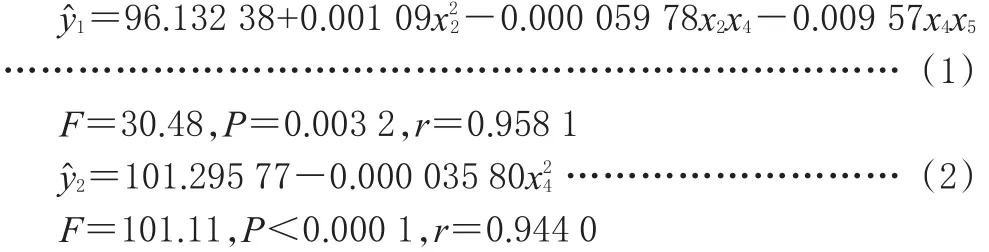
從公式（1）、（2）可知，兩個目標值與因素之間擬合出的模型效果均良好，遺傳算法可利用此模型進行兩個目標值的優化分析。

2.3 單目標及多目標遺傳算法的參數設置

分別以y1和y2為目標函數，用單目標遺傳算法分別搜索藥物包封率最大值的工藝條件及產物平均粒徑最小值的工藝條件：初始種群為30、單點交叉概率為0.9、單點變異概率為0.01、最大進化代數為100，分別進行10次隨機搜索。用VEGA進行兩目標優化，參數設置同單目標優化，進行12次隨機搜索。

2.4 軟件及統計方法

利用課題組編寫的Matlab 2009a外掛SGALAB工具箱Beta 5008完成遺傳算法尋優，需設置參數和方程，在Current directory窗口中，Input text處設置參數，設置參數有最大進化代數、初始種群、單點交叉概率、單點變異概率，在SGA.FITNESS.MO_function.m處設置方程，再打開遺傳算法程序SGALAB_demo_MO_VEGA.點擊運行鍵開始運行程序，即可得出適應度曲線圖與一組Pareto非劣解集。用SPSS 17.0軟件進行統計分析，對運行VEGA得到的Pareto非劣解集及目標函數值用中位數、四分位數間距來描述。

2.5 模型轉化

由于目標值產物y2要求得到最小值，而VEGA搜索得到的結果均為最大值，所以需將y2的模型進行轉換，y2′即為y2的最大轉化值，公式如下：

由公式（3）可知，用VEGA求得的最大轉化值y2′通過模型轉化即可求出y2的最小值y2。

2.6 VEGA搜索兩目標Pareto非劣解方案

以y1和y2作為兩個目標函數值，采用VEGA進行兩目標優化分析，以達到y1最大、y2最小的目的。從回歸模型公式（1）與（2）可看出，進入模型的因素有二氯甲烷x2、x4及x5，則VEGA搜索的因素也只有3個因素，結果詳見表2。

表2 VEGA兩目標隨機搜索結果Tab 2 Randomized search results of two-objective by VEGA

從表2可知，第2號與第12號試驗搜索的兩目標結果均較優，具有較大的包封率和較小的平均粒徑，VEGA兩目標隨機搜索聚乳酸載藥微球最優制備工藝即：2號試驗x2為86.68 mg/ml，x4為1499.48 r/min，x5為0.04%，y1最大達到 95.99%，y2最小達到20.80μm；也可選擇12號試驗工藝，即x2為89.98 mg/ml，x4為1498.96 r/min，x5為0，y1最大達到96.89%，y2最小達到20.86μm。可根據試驗的具體條件來選擇不同工藝。

兩目標最大適應度曲線見圖1，平均適應度曲線見圖2。

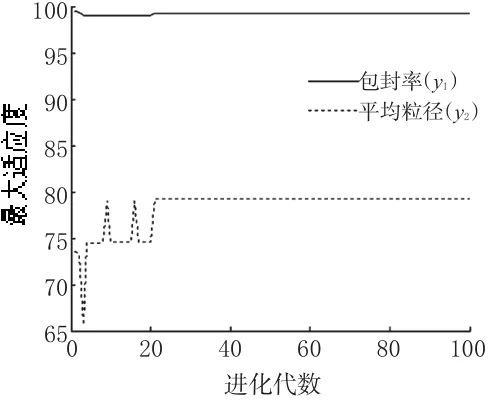
圖1 兩目標最大適應度曲線Fig 1 Two-objective maximum fitness-generation

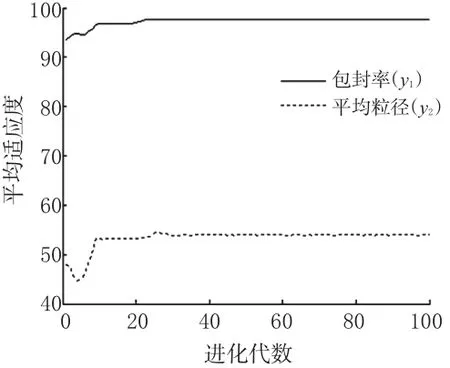
圖2 兩目標平均適應度曲線Fig2 Two-objectivemean fitness-generation

從圖1、圖2可知，VEGA在進化22代后y1和y2的最大適應度曲線和平均適應度曲線均達到穩定，分別反映出VEGA具有良好的收斂性和動態性。最大適應度進化曲線反映解的變化，用來評價算法的收斂性；平均適應度進化曲線用來評價遺傳算法的動態性能。

兩目標VEGA搜索的Pareto非劣解方案平均水平見表3。

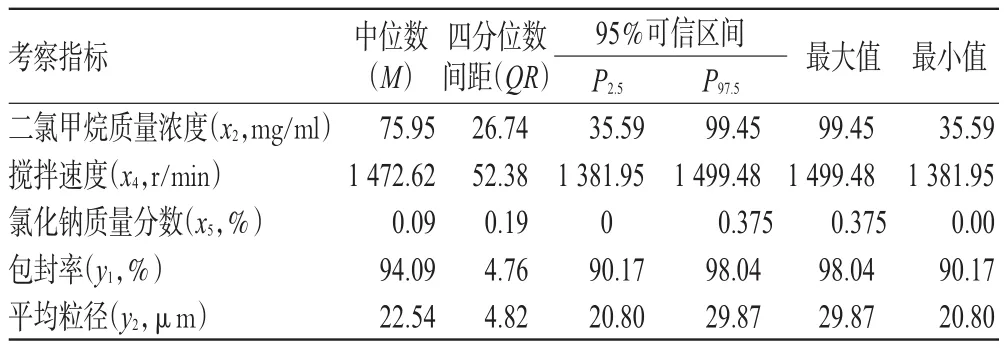
表3 兩目標VEGA搜索的Pareto非劣解方案平均水平Tab 3 Average level of Pareto non-inferior solution of VEGAtwo-objective

由表3可知，12次隨機搜索結果中，y195%可信區間的精度很高，其中位數為94.09%，四分位數間距為4.76%；y2的中位數為22.54μm，四分位數間距為4.82μm，95%可信區間的精度很高，由此可知VEGA的搜索結果是理想的。

2.7 VEGA兩目標遺傳算法與單目標搜索最優制備工藝的比較

單目標與VEGA兩目標Pareto非劣解方案的比較見表4。

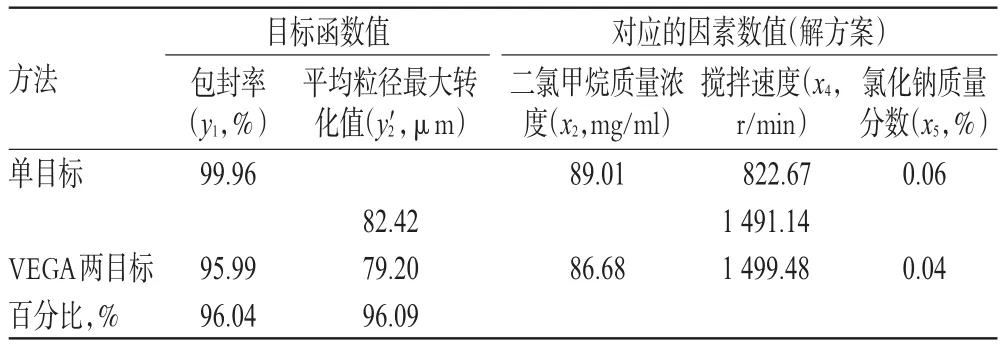
表4 單目標與VEGA兩目標Pareto非劣解方案的比較Tab 4 Comparison of Pareto non-inferior solution between single-objective and VEGAtwo-objective

從表4可知，VEGA兩目標遺傳算法搜索的目標函數值均小于單目標搜索的函數值，目標函數值偏低正體現了多目標遺傳算法的特點，因為多目標優化時將各子目標進行折中處理，盡可能獲得各子目標最大的解集[1]。VEGA兩目標搜索的y1達到單目標的96.04%，y2達到單目標的96.09%，VEGA遺傳算法的多目標搜索的結果達到了單目標最大函數值的96%以上，結果較為滿意。

2.8 VEGA兩目標遺傳算法與原文獻最優制備工藝的比較

原文獻數據利用均勻試驗設計，將8次試驗結果根據建立的二次回歸模型中一次項、二次項的符號，得出最優制備工藝為較高的x2、較高的x4及較低的x5，并無給出具體解集，這種結論帶有較強的主觀性。VEGA兩目標搜索出的最優工藝制備條件為y1最大達到95.99%，y2最小達到20.80μm，結果優于原文獻中均勻試驗設計的結果，并給出一組Pareto非劣解集，如表2中的12次隨機搜索結果，可供試驗者進行合理的選擇。

3 討論

VEGA搜索多目標問題時，能給出優化分析后的解集，即在因素范圍內尋出一組Pareto非劣解集，這正是VEGA比原文獻的優勢之處。對于實際問題的方案決策，必須依據客觀存在的條件，從Pareto非劣解中挑出一個或部分解作為所求大目標優化問題的最優解。結果表明：VEGA在均勻試驗設計藥物最優制備工藝選擇的應用是滿意的；確定的最優制備條件的效果較好，為研究者提供了精確度較高的試驗條件方案，可推廣到正交試驗設計、析因試驗設計的最優條件選擇。

[1]仇麗霞.基于遺傳算法的最優決策值選擇及醫藥學應用研究[D].太原：山西醫科大學，2007：1-3.

[2]王小平，曹立明.遺傳算法-理論、應用及軟件實現[M].西安：西安交通大學出版社，2001：115-117.

[3]Wu JZ，Hao XC，Chen FC，et al.A novel bi-vector encoding genetic algorithm for the simultaneous multiple resources scheduling problem[J].Journal of Intelligent Manufacturing，2012，23（6）：2255.

[4]崔遜學.多目標進化算法的研究及其應用[M].北京：國防工業出版社，2002：17-19.

[5]周建淞.基于向量評估遺傳算法的多目標優化效果評價及程序測試[J].中國衛生統計，2012，29（2）：181.

[6]曹婷穎，顧月清，高向東.聚乳酸載藥微球的制備和給藥方法[J].藥學進展，2006，30（10）：448.

[7]張海龍，高鈴美，邵洪偉.聚乳酸載藥微球的制備及應用研究進展[J].西北藥學雜志，2010，25（2）：158.

[8]林雅鈴.均勻試驗設計在水溶性藥物聚乳酸微球制備中的應用[J].中國醫院藥學雜志，2009，29（7）：531.