Nash均衡模型的船舶主尺度多目標優選

林少芬，楊貴強

(集美大學 輪機工程學院，福建 廈門361021)

0 引 言

船舶主尺度優選方案中，必須全面考察船舶各項技術性能、經濟性，注意主尺度的選擇對技術、經濟指標的影響程度［1］，多目標的船型優選屬于非線性函數優化范疇。傳統的多目標優化方法有梯度法、牛頓法和直接法等，這些方法繼承了求解單目標問題的一些成熟算法和機理，但對于性質復雜不清的目標函數難以適用［2-3］。

在船型多目標優化過程中，設計者考慮多個性能技術指標，各目標之間相互沖突，難以找到一個最優的非劣解，只有綜合考慮各目標函數的性質，才能得到最優均衡解。本文依據博弈理論，將運輸成本TC和年運貨量AC作為優化目標博弈方，運用非合作Nash 均衡博弈模型來平衡多目標之間的沖突和競爭，以Nash 均衡狀態解作為最優解。

1 博弈論算法求解多目標優化

1.1 多目標優化問題的博弈描述

多目標優化問題是將n 個設計變量映射到m 個目標函數的向量函數，數學模型表示為:

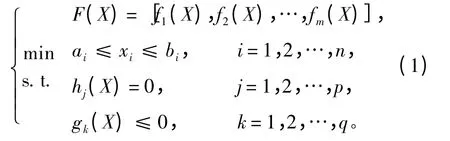
式中:［x1，x2，…，xn］∈X 為設計變量;bi和ai為設計變量xi的上下限;p和q 分別為等式約束和不等式約束的個數。

將多目標問題轉化為博弈策略問題，m 個設計目標看作是m 個博弈方，設計變量集X 視為博弈論中的策略空間S1，S2，…，Sm，多目標函數的約束視為博弈問題中的約束條件，通過某一方案優化后的結果可作為相應博弈方的得益。因此，式(1)中的多目標優化問題轉化為對博弈問題G 的描述:

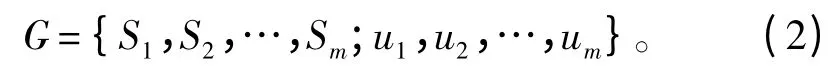
式中:u1，u2，…，um為m 個優化目標即博弈方，并滿足:

1.2 Nash 均衡定義描述

1.3 基于Nash 均衡模型的求解步驟

求解步驟如下:

1)通過設計變量對博弈方得益的計算，得到隸屬于各博弈方的策略集S1，S2，…，Sm;

2)在各博弈方策略集組合Si中隨機生成初始可行策略組合為s0={s10，s20，…，sm0};

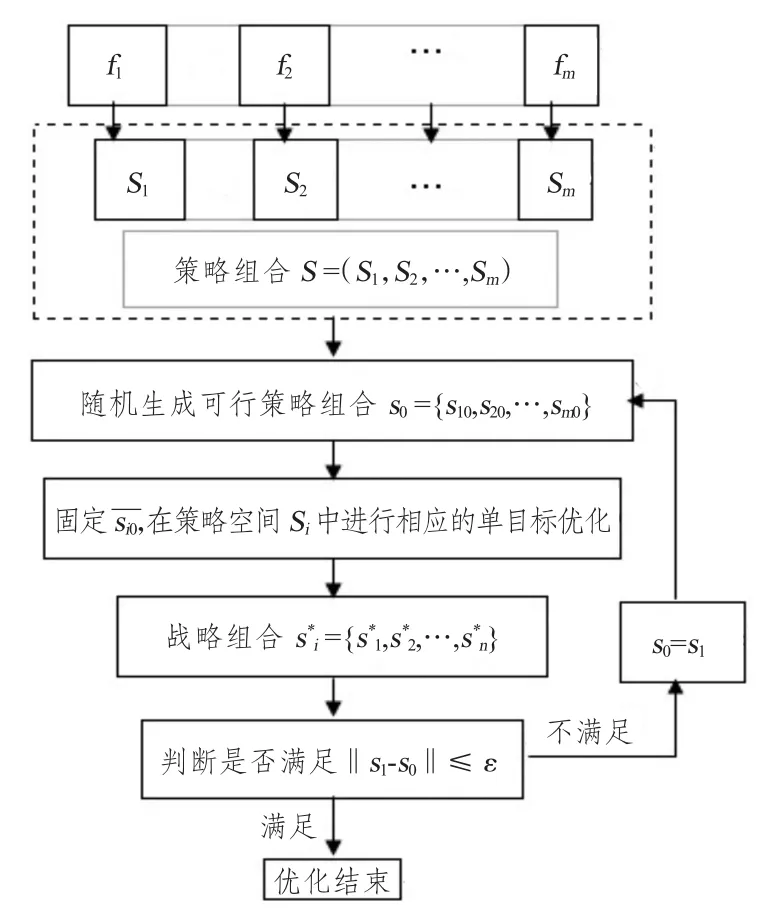
圖1 Nash 均衡計算步驟Fig.1 Computing steps of nash equilibriu

1.4 博弈方策略空間計算

博弈理論分析多目標優化問題的關鍵技術在于將設計變量集X 分解為各博弈方擁有的策略空間S1，S2，…，Sm。本文通過計算設計變量對博弈方得益的影響因子指標，并對該指標進行模糊聚類，得到隸屬于各博弈方的策略空間S1，S2，…，Sm。

計算步驟如下:

2)設計變量xj對第i 個博弈方ui的影響因子

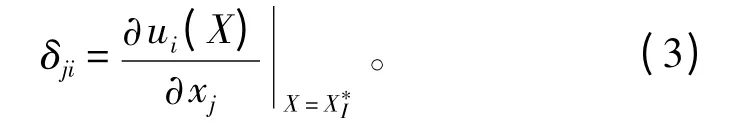
若無法通過目標函數偏倒計算影響因子，也可通過數值方式計算影響因子:在設計變量xj的可行空間中，按步長δj分為T 等段，則設計變量xj對第i個博弈方ui的影響因子:

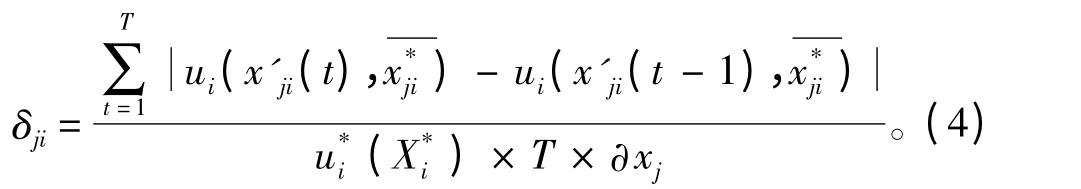
3)δj={?ji，?j2，…，?jm}(j=1，2，…n)為分類樣品表達式，δj為第j 個設計變量對所有m 個目標的影響因子集合。分類樣品全體集合為?={?1，?2，…，?n}，對?進行模糊聚類［8］，將設計變量集X 分解為各博弈方的策略空間S1，S2，…，Sm。

2 算例分析

利用文獻［9-10］中的設計數據，本文考慮6個設計變量、2 個目標函數和11 個約束條件的多目標散貨船船型優選問題。設計變量選定為船長L、船寬B、型深D、吃水T、方形系數CB及經濟航速VK，設計變量集為x={L，B，D，T，CB，VK}T，計算模型見附錄。

目標函數運輸成本TC和年運貨量AC作為博弈方，

式中:Whw為貨物重量;RTPA 為每年周轉次數;My為年費用。要求運輸成本TC最小和年運貨量AC最大。

約束條件選定:

25 000 ≤DWT ≤500 000;L/B ≥6;L/D ≤6;L/T ≤19;T ≤0.45DWT0.31;T ≤0.7D+0.7;0.63 ≤CB≤0.75;L ≤274.32;14 ≤VK≤18;Fn ≤0.32;GMT=KB+BMT- KG ≥0.07B。

式中:DWT 為載重量;Fn 為傅汝德數;GMT為初穩性高;KB 為浮心高;BMT為穩性半徑;KG 為重心高度。

2.1 策略空間計算

1)采用序列二次規劃(SQP)分別對目標函數TC和AC進行單目標優化，優化結果如表1所示。

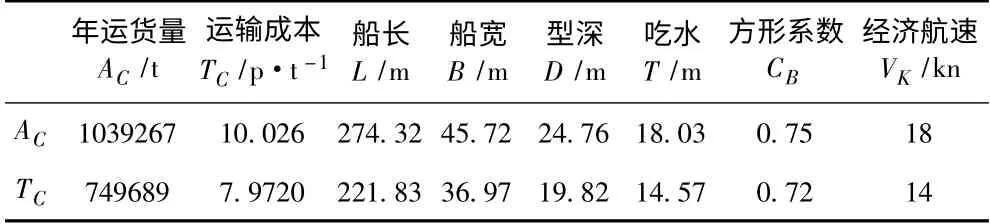
表1 單目標優化計算結果Tab.1 Computing results of single-objective optimization

2)根據式(3)，分別對目標函數求偏導，依據單目標優化結果計算影響因子:

δL={906.7551，0.0075};δB={6235.1，-0.0081};δD={-692.5211，-0.0748};δT={17492，-0.2089};δCB={376069，1.5098};δVK={12106，0.2020}。

3)模糊聚類分析

δ={δL，δB，δD，δT，δCB，δVK}={δ1，δ2，δ3，δ4，δ5，δ6}為影響因子全體，每個因子δi由一組數據{δi1，δi2}表征。建立δ 的模糊相似矩陣R=(rij)6×6，其中xi和xj的相似度 rij采用絕對值減數法 rij=計算［11］，則相似矩陣R 計算結果為:

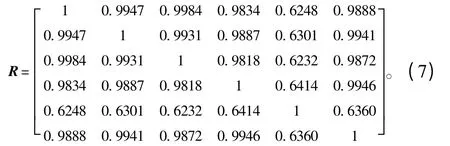
采用傳遞閉包法得:

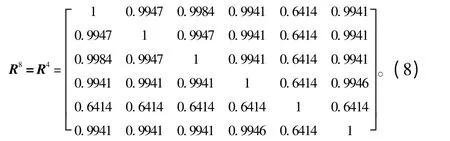
所以R4是R 的傳遞閉包t(R)。設為模糊等價矩陣，結合目標函數數量，取截值λ=0.9941，將δ 分成2 類:

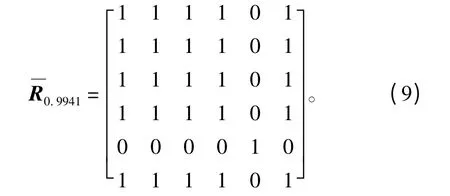
經模糊聚類的結果得:博弈方年運貨量AC的策略空間S1={L，B，D，T，VK}，博弈方運輸成本TC的策略空間S2={CB}。

2.2 Nash 均衡計算

分別以策略空間S2的參數優選S1的5 個參數(即以運輸成本TC的優選參數值CB作為年運貨量AC優化的初始值)和以S1的參數優選S2的參數進行Nash 均衡求解，循環次數為200，得到200 個非劣解，TC和AC之間的非劣解的散點圖分布如圖2和圖3所示。

將圖2 中年運貨量AC最大值用直線連接，根據運輸成本TC由小到大得到5 個備選方案，具體參數見表2。圖3 散點成線性分布，根據年運貨量由大到小得到5 個備選方案(見表3)。

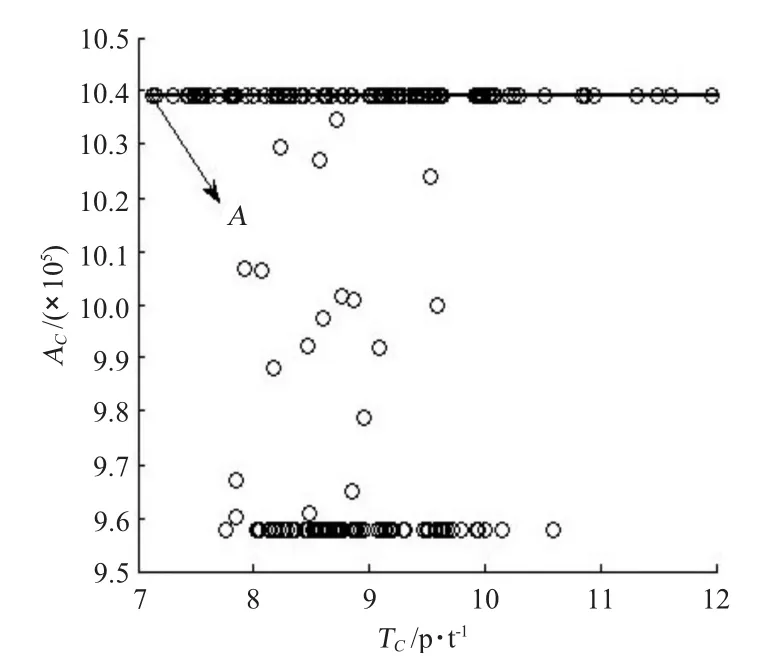
圖2 非劣解散點圖Fig.2 Scatter plot of non-inferior

圖3 非劣解散點圖Fig.3 Scatter plot of non-inferior

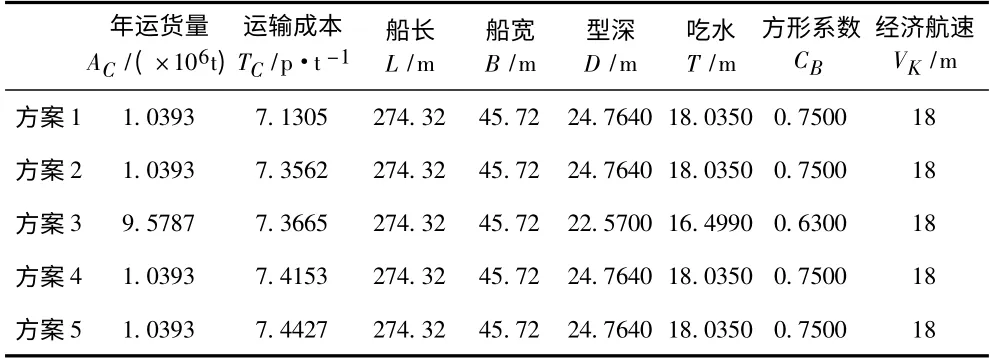
表2 Nash 均衡博弈模型優化結果Tab.2 Optimization solutions of nash equilibrium model

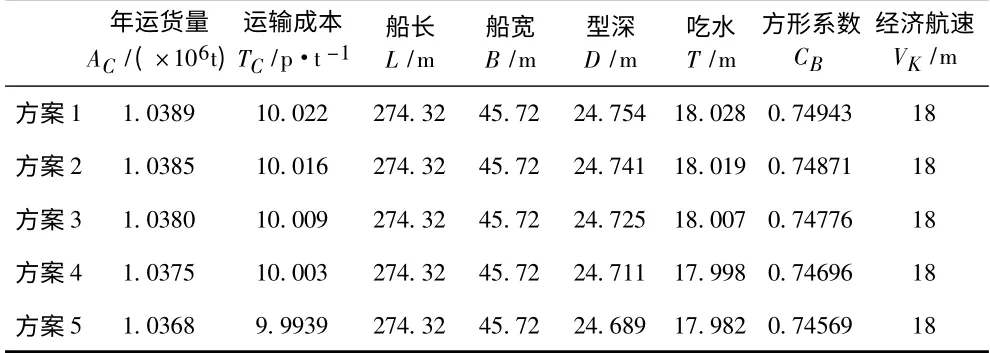
表3 Nash 均衡博弈模型優化結果Tab.3 Optimization solutions of nash equilibrium model

從多目標優化問題定義講，圖2和圖3 中的解都能作為式(1)的可行解，不同的優選方案得到不同的理想解。圖2 優選結果明顯優于圖3，圖2 中方案A(即表2 中方案1 的優選參數)為得益最佳的優選方案，滿足運輸成本T 最小和年運量AC最大。通過與文獻［2］的比較，應用Nash 均衡策略求解多目標問題非劣解，可操作性強，較Pareto 解集更易控制。

非合作Nash 均衡博弈指各博弈方以競爭方式，并以自身的最佳得益為決策目標，其博弈結果可能對其他博弈方不利。通過計算策略空間的Nash 均衡解較優，但不能使各博弈方和整體性達到最優。

3 結 語

本文以散貨船的年運貨量、運輸成本為主要目標進行了主尺度方案的優選。通過對比結果可知，Nash均衡博弈法能夠快速、有效地選擇船舶主尺度，對于不同的設計要求，能使各目標函數以自身的得益最大為目標，獲得各目標函數之間的最優均衡解。在船型方案的優選中，為設計者提供更多的選擇方案。

［1］顧敏童.船舶設計原理［M］.上海:上海交通大學出版社，2001.

［2］潘治，李學斌.改進的多目標優化算法及其在船舶設計中的應用［J］.中國造船，2010，51(2).

［3］李文龍，譚家華.集裝箱船主尺度全局最優化的混沌算法［J］.中國造船，2003(1).

［4］張宏波，顧鐳，徐有忠.基于博弈論的汽車耐撞性多目標優化設計［J］.汽車工程，2008，30(7):553-556.

［5］徐立哲，岑豫皖，謝能剛，等.基于Nash 均衡博弈模型的銑削參數多目標優化設計［J］.裝備制造技術，2009(9).

［6］陳忠，謝能剛，張子明.結構多目標優化設計的合作博弈解法［J］.工程力學，2009，26(4):32-36.

［7］楊二波，陳明.船舶主尺度方案的博弈優選［J］.中國艦船研究，2010，5(6).

［8］XIE Neng-gang，SHI Na，BAO Jia-han.Analysis and application of multi-object decision design based on game theory［C］.6th World Congresses of Structural and Multidisciplinary Optimization.Rio de Janeiro Brazil，2005.

［9］SEN P，YANG J B.Multiple criteria decision support in engineering design［M］.Spinger，London，1988.

［10］PARSON M G，SCOTT R L.Formulation of multicriterion design optimization problems for solution with scalar numerical optimization methods［J］.Journal of Ship Research，2004，48(1):61-76.

［11］張弢，紀德云.模糊聚類分析法［J］.沈陽大學學報，2000，12(2):73-79.