懸臂梁橋中鉸最佳位置的確定
劉春雷,戴素娟,2,劉春暉,2
(1.山東科技大學,山東 青島 266590;2.山東省土木工程防災減災重點實驗室,山東 青島 266590)
1 概 述
隨著我國社會經濟的不斷發展,橋梁建設進入高速發展時期,當今的道路和橋梁的建設投資規模越來越大,相關施工技術水平要求越來越高,結構復雜程度逐漸加深。科學合理的技術方案,不僅能夠確保工程質量,還可以提高經濟效益[1]。
橋梁工程中簡支梁橋是應用廣泛的結構形式之一,是建橋實踐中受力和構造最簡單的橋型。跨度較大的橋梁,跨中恒載彎矩和活載彎矩明顯增大,導致梁的截面尺寸和自重顯著增加,不但耗費大量材料,不經濟,而且會造成施工困難[2]。因此,研究減小橋梁跨中彎矩體系,是橋梁設計中值得探討的重要問題。
懸臂梁橋的內力不受基礎不均勻沉降等附加變形的影響,由于布置伸臂梁,它一方面減少了附屬部分梁的跨度,另一方面使得伸臂上的荷載對簡支部分產生負彎矩,從而抵消橋梁跨中荷載產生的正彎矩[3]。為使懸臂梁橋的最大彎矩值減小,需確定伸臂梁中鉸的最佳位置,當梁的最大正負彎矩值的絕對值相等時,可獲得最佳的經濟效益。
2 兩跨懸臂梁橋中鉸位置的分析
橋梁常用主次梁結構,其中常承受恒載和活載的作用,普通橋梁設計時次梁一般不多。本文以實際工程中常用的兩跨懸臂梁橋為分析對象,研究其在各種荷載作用時的內力分布規律。圖1為兩跨跨度為l 的懸臂梁橋的計算簡圖。懸臂梁橋的最大正負彎矩值與伸臂梁中鉸的位置有關。通過調節鉸的位置,使最大正負彎矩值的絕對值相等,達到減小梁中最大彎矩的目的。
2.1 一跨跨中作用集中荷載時
對兩跨梁分析可知,集中荷載作用在基本部分時,附屬部分無影響。因此,所做的彎矩圖和彎矩的最大值與簡支梁一樣,得出梁的最大彎矩值與鉸的位置無關。
2.2 二跨跨中均有荷載作用時
2.2.1 二跨跨中均作用單個集中荷載時(見圖2)
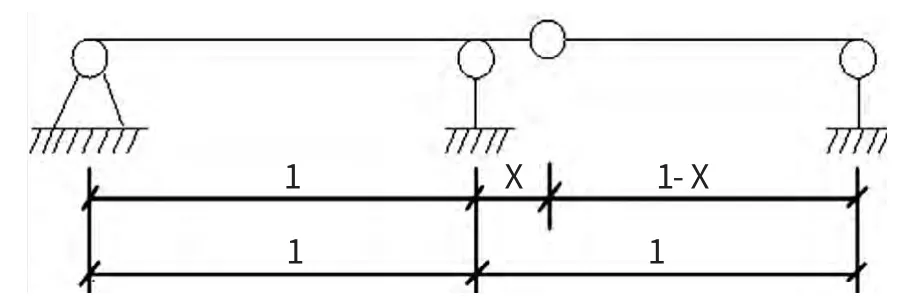
圖1 懸臂梁橋計算簡圖
將FRC與FRD的表達式代入該式,得
2.2.2 二跨跨中分別作用等間距布置的多個集中荷載和均布荷載時,經分析可得多個集中荷載作用時的最大彎矩值和值,列于表1中
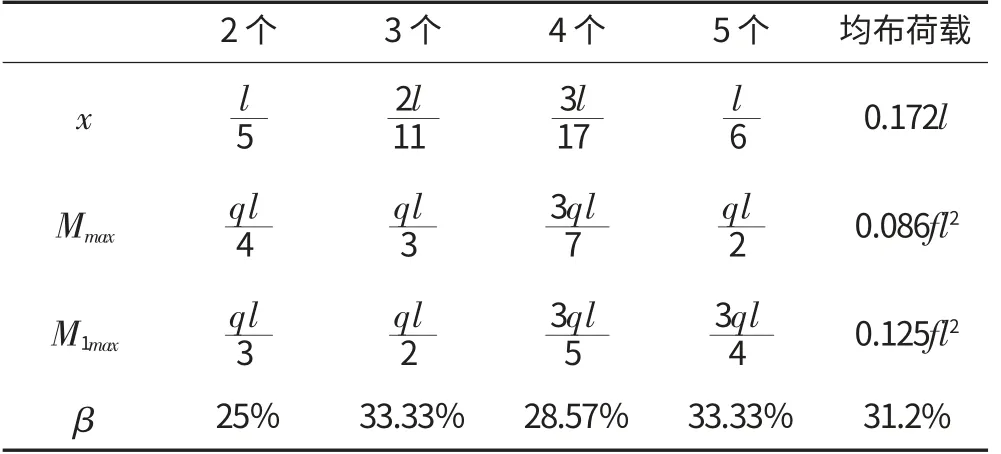
各種荷載作用下的最大彎矩值和鉸的最佳位置 表1
表1中:q 是集中荷載;f 是均布荷載;l 是相鄰支座的距離;x 是與最近支座的距離;Mmax是最大彎矩值;M1max是簡支梁的最大彎矩值;β 是懸臂梁橋的最大彎矩值比簡支梁橋的最大彎矩值減小的百分比。
從上可知,當梁上作用有等間距布置的集中荷載時,選取合適的鉸的位置可使懸臂梁橋的最大彎矩值減小大約30%,其內力分布更加均勻。
對于多跨懸臂梁橋的內力和鉸的位置的計算,可用相同的力學原理求得。
3 結 論
本文分析了實際工程中常用的二跨懸臂梁橋承受單個集中荷載、等間距布置的多個集中荷載和均布荷載作用的情況,根據最大正負號彎矩值的絕對值相等為已知條件,得出了橋梁在受到單個集中荷載、多個集中荷載和均布荷載作用時鉸的最佳位置。當梁上作用等間距布置的集中荷載和均布荷載時,可使梁中最大彎矩值減小大約30%,為相似橋梁和工程的優化設計提供了一定參考。
[1]師云連.淺談懸臂支撐體系進行梁體體系轉換的施工技術[J].門窗,2012(10).
[2]邵旭東,顧安邦,等.橋梁工程(第二版)[M].北京:人民交通出版社,2007.
[3]李廉錕.結構力學(上冊)(第五版)[M].北京:高等教育出版社,2009.

