兩類積分的求解*

姜培華，吳 玲，紀習習

(安徽工程大學數理學院，安徽 蕪湖 241000)

本文討論了兩類積分的簡便求解問題，兩類積分如下:

1 積分(1)的求解

對于上述積分(1)若直接考慮一重積分的方法求解，實屬不易，因為對于這樣的被積函數很難利用湊微分法和分部積分法來解決，為此只好另辟蹊徑．本文下面考慮四種辦法來解決此問題．

首先給出下面的引理1．

引理1 對于實數a∈R+下述積分等式成立:

證明 (ⅰ)給定下述三個平面區域:D1?D2?D3，其中:

L3=(1－e－2aR2)．又因當R→+∞時由夾逼準則可知當R→+∞時，有從而可得結論(ⅰ)成立．

(ⅱ)給定下述三個空間區域:Ω1?Ω2?Ω3，其中:

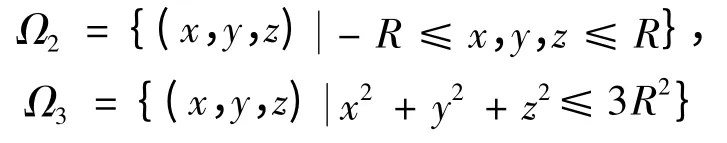
1)二重積分法

考慮到I2并利用引理1的結論(ⅰ)可得:

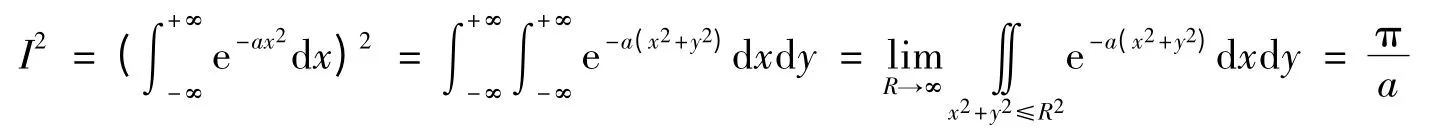
2)三重積分法

考慮到I3并結合引理1中的結論(ⅱ)可得:

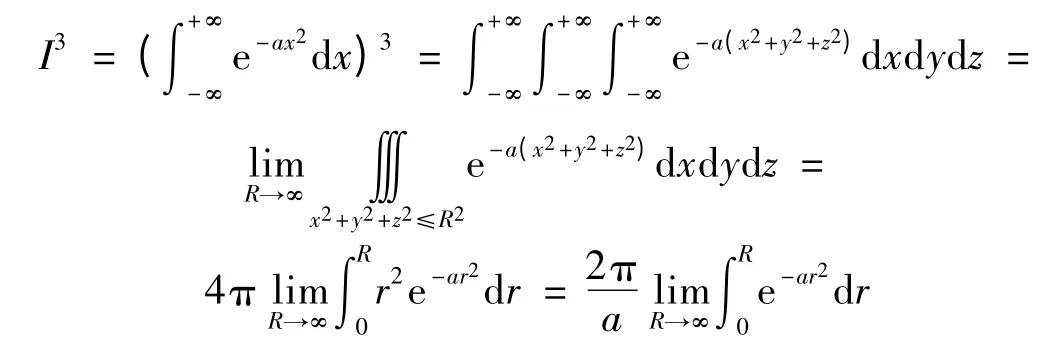
即有:

3)伽瑪函數法

首先給出伽瑪函數的定義和性質，其定義和性質在諸多文獻［1，2］中都有介紹．稱以下函數

為伽瑪函數，其中參數α＞0．伽瑪函數具有如下性質:

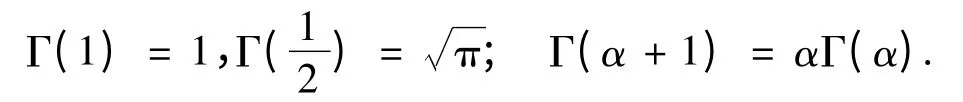
下面求解此積分:

令y=x2對式(4)作變換可得:

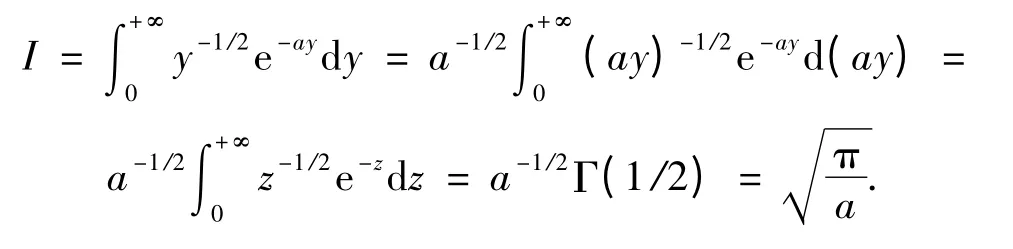
式中z=ay．

4)概率方法

構造正態隨機變量X～N(0，1/2a)，則其密度函數為:

對于積分(1)推廣到如下形式:

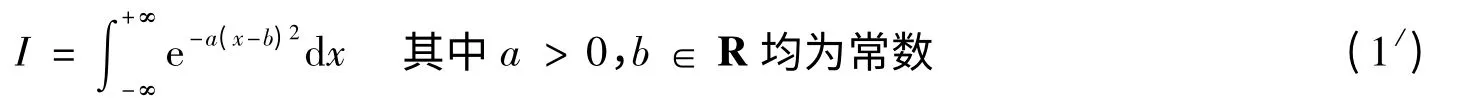
綜上可以看出對于積分(1)考慮到被積函數的形式特點和積分區域的特性，運用概率方法，構造一個適當的概率密度去求解積分，比運用代數方法和分析方法求解要簡潔明了．它使數學的不同分支之間架起了橋梁．

2 積分(2)的求解

對于積分(2)很容易看出其是一個定積分，與積分(1)有很大的區別，其積分上下限都是有限值．在這種情況下如果再利用二重積分法、三重積分法和伽瑪函數法都不能夠解決，為此考慮用概率方法并結合查標準正態分布的概率分布表來解決．

記X～N(0，1)，其概率密度函數和分布函數分別記為φ(x)和Φ(x)．根據積分(2)中被積函數的特點可以構造一個非標準的正態密度函數來表示積分(2)，考慮到積分(2)的積分限都是有限數，進而可以利用正態分布的標準化來查概率分布表求解．基于上述分析可得:

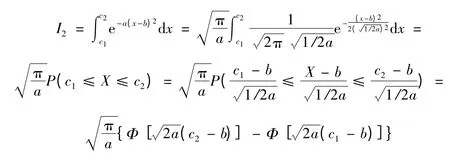
式中X～N(b，1/2a)．

當參數a，b，c1，c2已知時，可以通過查標準正態分布的概率分布表來計算該類積分．

3 應用舉例

例1［3］證明不等式:

證明 設X與Y獨立同分布于標準正態分布N(0，1)，記區域D1，D2分別為:

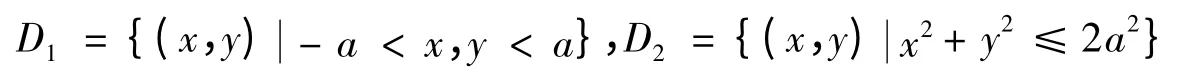
易知D1?D2，故有P{(X，Y)∈D1}＜P{(X，Y)∈D2}，考慮到X與Y獨立即有:

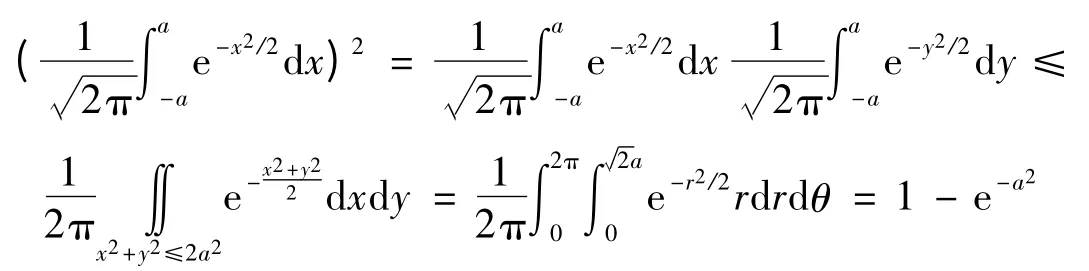
例2［4］已知X，Y相互獨立，X～U(0，1)，Y的概率密度為fY(y)=，y＞0，設a的二次方程a2+2Xa+Y=0，求其有實根的概率．

解 由獨立性可求出(X，Y)的聯合概率密度函數為:

由韋達定理可知方程有實根的概率為:

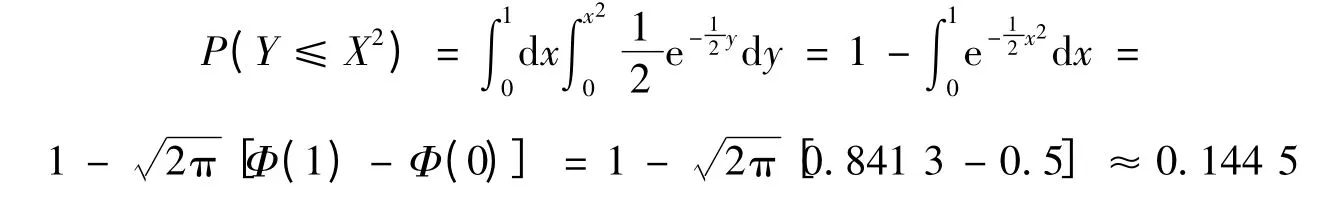
［1］同濟大學應用數學系．高等數學(上)［M］．第5版．北京:高等教育出版社，2002．

［2］茆詩松，程依明，濮曉龍．概率論與數理統計教程［M］．北京:高等教育出版社，2004．

［3］Peter－Bickel J．數理統計—基本概念及專題［M］．李澤慧，李效虎，荊炳義，譯．蘭州:蘭州大學出版社，2005．

［4］項立群，汪曉云，梅春暉，等．概率論與數理統計［M］．北京:北京大學出版社，2011．