形狀記憶合金三維鼓包結構熱變形的有限元模擬

趙澎濤，裘進浩，于慧臣

（1.北京航空材料研究院航空材料檢測與評價北京市重點實驗室，先進高溫結構材料重點實驗室，北京100095；2.南京航空航天大學機械結構力學及控制國家重點實驗室，南京210016）

0 引 言

形狀記憶合金（SMA）同時具備感知和驅動功能，可以感知外界的溫度變化，并能夠將熱能轉化為機械能，其以優異的形狀記憶效應、偽彈性［1-2］、生物相容性和阻尼特性，廣泛應用于航空航天［3-4］、生物醫藥［5］、土木工程［6］等領域。但由于SMA 復雜的熱力學耦合關系，其本構關系不能用通常的彈塑性模型描述，因此SMA 本構行為的描述是目前研究的熱點和難點。為了實現SMA更廣泛的工程應用，作者以SMA在三維自適應發動機進氣道變體結構中的應用為研究背景，利用SMA所特有的形狀記憶效應，使用溫度控制的方式實現了鼓包結構的變形。通過建立SMA三維本構關系模型，采用回歸映射應力更新算法進行有限元實現，并對SMA三維鼓包結構在熱變形過程中的熱力學特性響應進行有限元分析，得到了一定溫度條件下該結構的變形參數，為SMA在發動機進氣道中的應用提供支持。

1 SMA的本構關系模型

采用Lagoudas關于SMA的三維唯象理論模型［7-8］，即SMA在變形過程中產生的應變主要由彈性應變、熱膨脹應變和相變引起的應變等三部分構成，假設SMA的Gibbs自由能（G）為

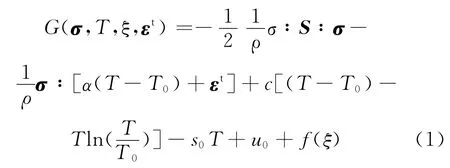
式中：σ，εt，ξ，T 以及T0分別為真實應力張量、相變應變張量、馬氏體體積分數、溫度以及參考溫度；S，α，ρ，c，s0和u0分別為等效柔度張量、等效熱膨脹系數、密度、等效比熱、參考溫度下的等效比熵和參考溫度下的等效內能；f（ξ）為相變硬化函數，表征了馬氏體相與母相或者馬氏體變體之間發生相互轉化而產生的應變能。

以上各等效材料特性參數可由材料中所含的馬氏體體積分數以及純晶體相的特性參數計算得到，其具體的表達式如式（2）。式中物理量右上角處的A與M分別表示為奧氏體相和馬氏體相：

結合熱力學相關理論，SMA的本構關系及約束條件可以從Gibbs自由能推導得到，其表達式如式（3）和式（4）：

假設在馬氏體相變過程中忽略馬氏體變體的重定向過程，材料任何微觀狀態的改變都僅僅是馬氏體含量變化的結果。基于此假設，SMA相變過程中的相變應變εt和馬氏體體積分數ξ的演化方程（類似于塑性力學理論中的流動法則）可表示為

式中：Λ為相變轉換張量，表征了相變應變的方向。

將相變演化方程式（5）代入式（4）的本構關系約束條件中，可得到：

式中：π為與馬氏體體積分數ξ共軛的熱驅動力。

將Gibbs自由能的顯示表達式（1）代入上式，可得到：

基于以上關于馬氏體正逆相變的假設以及邊界條件的表述，引入相變函數φ（相當于塑性力學中的屈服函數），其表達式為

式中：Y為相變臨界屈服值。

基于不同相變過程的假設，SMA唯象理論模型可以通過不同的相變硬化函數來表征。Tanaka指數形式理論模型［9］、Liang和 Rogers余弦模型［10］以及Lagoudas多項式模型［7］的硬化函數分別見式（9），（10），（11）：

2 UMAT材料子程序的編寫及驗證

在Lagoudas的SMA三維本構關系模型的基礎上，利用ABAQUS的二次開發功能編寫FORTRAN程序［11］實現SMA的有限元模擬。

針對前面提到的SMA本構關系模型，在UMAT中定義了13個變量（1為馬氏體體積分數、2～7為相變應變分量，8～13為個相變方向）和20個材料常數（1～2為彈性模量，3～4為熱膨脹系數，5～8為相變溫度，9～10為應力影響參數，11～16為初始相變應變，17為最大相變應變，18為泊松比，19為容差，20為初始馬氏體體積分數）。

為了驗證編寫的UMAT子程序的準確性，在ABAQUS軟件中建立受單軸加載的單元模型，如圖1所示，一端固支約束，一端加載軸向力載荷。載荷加載歷史如圖2所示。模型中的SMA材料參數采用文獻［12］中的等原子鈦鎳合金參數，即：奧氏體相彈性模量EA為70GPa，馬氏體相彈性模量EM為30GPa，泊松比νA和νM均為0.3，奧氏體相膨脹系數αA為22×10-6K-1，馬氏體相膨脹系數αM為22×10-6K-1，馬氏體相變開始溫度Ms為291K（18℃），馬氏體相變結束溫度Mf為280K（7℃），奧氏體相變開始溫度As為295K（22℃），奧氏體相變結束溫度Af為306K（33℃），最大相變應變H為0.05。針對超彈性的驗證，模型初始相為奧氏體，初始溫度為325K（52℃），單軸最大載荷為60kN。針對形狀記憶效應的驗證，模型初始相為馬氏體，初始溫度為292K（19℃），單軸最大載荷為30kN，加載結束后升溫至350K（77℃），高于奧氏體相變結束溫度。

圖1 單軸加載模型示意Fig.1 Abridged general view of uniaxial loading model

圖2 載荷加載歷史示意Fig.2 Abridged general view of applied load history

從圖3，4可以看出，以上基于不同硬化函數的三種本構關系模型都能夠較好地描述SMA的超彈性和形狀記憶效應等特性，相變過程也遵循相應的馬氏體奧氏體相變模型表征函數，證明了該UMAT子程序的正確性，從而保證了在UMAT子程序基礎上進行的鼓包熱變形模擬結果的準確。

圖3 基于不同硬化函數的SMA超彈性模型的模擬結果Fig.3 Simulated results of SMA pesudoelasticity model based different hardening functions

圖4 基于不同硬化函數的SMA形狀記憶效應的模擬結果Fig.4 Simulated results of SMA shape memory effect based different hardening fuctions

3 有限元模擬結果與討論

3.1 有限元模型的建立

SMA鼓包熱變形模型是三維薄壁球體結構的一部分，其尺寸參數包括：過中心點A的弧線在x-z平面上的投影長（圖5中的BC線段，10cm）、鼓包厚度（1mm）、曲率半徑（42cm）。該鼓包模型在經歷雙程記憶效應訓練之后，沿過中心點的徑長方向具有高溫伸長、低溫收縮的性質。模型網格劃分采用了減縮積分的線性六面體單元（C3D8R），在厚度方向上劃分5個單元，以免產生沙漏效應。材料參數與前面驗證模型中采用的參數相同。

圖5 三維鼓包熱變形模型的網格劃分Fig.5 Meshing of the three demensional bump thermal deformation model

鼓包熱變形模型邊界條件為周邊固支約束，初始溫度為291K（18℃），初始狀態為馬氏體相。沿過中心點的弧長方向具有初始的相變應變，根據不同的訓練效果分為-0.5%，-1%，-1.5%，-2%幾種情況。考慮鼓包沿厚度方向的初始相變應變，初始馬氏體體積分數為1。結構的網格劃分如圖5所示。SMA鼓包表面加載溫度載荷，從初始溫度291K（18℃）加載至360K（87℃）并保持溫度，增量加載步數為100步，具體過程如圖6所示。

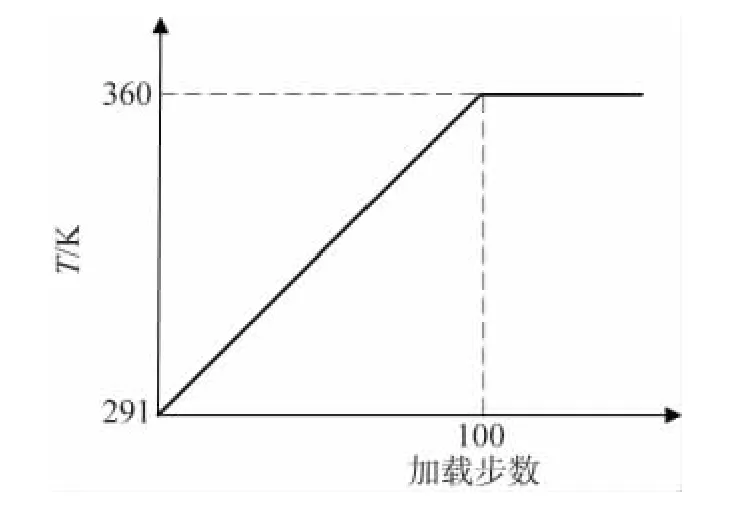
圖6 溫度加載歷程示意Fig.6 Abridged general view of temperature loading history

3.2 模擬結果與討論

3.2.1 定初始相變的SMA鼓包相變特性

從圖7中可以看出，鼓包模型在初始狀態時為純馬氏體相，體積分數為1；隨著溫度的逐漸升高，在鼓包中部馬氏體相的體積分數開始下降，并逐步向鼓包的四周邊界擴展；加載結束后鼓包的大部分區域基本完成了馬氏體逆相變，轉化為奧氏體相，只有在接近固支約束的邊界部分仍殘留有馬氏體相。

從圖8中可以看出，圖5中的A、B兩點在297K（24℃）左右開始向奧氏體相轉變，A點在313K（40℃）結束了馬氏體逆相變過程，馬氏體體積分數為0，全部轉化為奧氏體相；而在B點，由于邊界條件的約束，限制了鼓包的馬氏體逆相變過程，在加載結束后仍殘留有部分馬氏體相。

3.2.2 定初始相變應變的SMA鼓包熱變形力學特性

由圖9可見，A點的豎向撓度在初始階段增長較慢，在23～40℃（296～313K）的溫度區間增長較快，并且大部分的撓度變化發生在該區間內，而且該區間與馬氏體逆相變的溫度區間相近。可知，鼓包豎向撓度的產生主要與SMA的相變有關。

3.2.3 不同初始相變的SMA鼓包熱變形結果

鼓包在加載過程中最大豎向撓度發生在加載結束溫度360K。由圖10可見，最大豎向撓度與初始相變應變絕對值之間基本呈線性正比關系。當初始相變應變絕對值為2%時，鼓包最大的豎向撓度達到了5mm，相當于鼓包模型BC線段長度的5%。

圖7 初始相變應變為-1%時，SMA鼓包模型在不同溫度下的馬氏體體積分數云圖Fig.7 Martensite fraction of SMA bump model at initial phase-transformation strain of-1%and different temperatures

圖8 SMA鼓包模型中不同位置處在不同溫度下的馬氏體體積分數Fig.8 Volume fractions of martensite vs temperture for different locations in SMA bump model

圖9 SMA鼓包中心A點處的豎向撓度隨溫度的變化Fig.9 Change of vertical deflection of the point A（in the middle of the SMA bump）with temperature：（a）vertical deflection of bump and（b）vertical deflection of point A

圖10 SMA鼓包在加載過程中最大豎向撓度與初始相變應變絕對值之間的關系Fig.10 The relation ofmaximum vertical deflection and initial phase-transformation strain during SMA bump

從圖11中可以看出，在一定的初始相變應變下，隨著溫度的升高，豎向高度曲線的形狀和最大高度也發生改變；豎向高度在313K（40℃）之后的變化較小，該溫度與鼓包中A點相變結束點的溫度基本吻合。

圖11 SMA鼓包過A點弧線各點在不同初始相變下的豎向高度曲線Fig.11 Vertical height curves of the points which pass by the point A at different initial phase-transformation strains

3 結 論

（1）通過ABAQUS軟件材料子程序UMAT的接口，編寫FORTRAN程序，將SMA的本構關系模型導入到ABAQUS材料庫中，從而使有限元軟件具備了對SMA模型進行數值模擬的能力；通過建立SMA單軸受力模型，證明了材料子程序UAMT能夠同時描述SMA的超彈性和形狀記憶效應特性。

（2）對于三維鼓包熱變形模型，馬氏體逆相變首先發生在鼓包的中部并向四周擴展，除邊界部分未完成逆相變外，其余大部分完全轉化為奧氏體相；鼓包的撓度最高達到5mm，相當于其弧線投影長度的5%。

致謝：

感謝南京航空航天大學機械結構力學及控制國家重點實驗室的鼎力支持。

［1］MIRZAEIFAR R，SHAKERI M，SADIGHI M.Nonlinear finite element formulation for analyzing shape memory alloy cylindrical panels［J］.Smart Materials and Structures，2009，18（3）：1-14.

［2］LAGOUDAS D C.Shape memory alloys：modeling and engineering applications［M］.New York：Springer，2008：1-43.

［3］GAO X，TURNER T L，BURTON D，et al.Finite element analysis of adaptive-stiffening and shape-control SMA hybrid composites［J］.Journal of Engineering Materials and Technology，2006，128（3）：285-293.

［4］REY N，TILLMAN G，MILLER R，et al.Shape memory alloy actuation for a variable area fan nozzle［C］//Proceedings of SPIE，Smart Structures and Materials：Industrial and Commercial Application of Smart Structures Technologies.［S.l.］：［s.n］，2001：371-382.

［5］徐祖耀，江伯鴻.形狀記憶材料［M］.上海：上海交通大學出版社，2000：3-6.

［6］WILLIAMS K，CHIU G，BERNHARD R.Adaptive-passive absorbers using shape-memory alloys［J］.Journal of Sound and Vibration，2002，249（5）：835-848.

［7］BO Z，LAGOUDAS D C.Thermomechanical modeling of polycrystalline SMAs under cyclic loading-Part I：theoretical derivations［J］.International Journal of Engineering Science，1999，37：1089-1140.

［8］QIDWAI M A，LAGOUDAS D C.On thermomechanics and transformation surfaces of polycrystalline NiTi shape memory alloy material［J］.International Journal of Plasticity，2000，16：1309-1343.

［9］TANAKA K，NISHIMURA F，HAYASHI T，et al.Phenomenological analysis on subloops and cyclic behavior in shape memory alloys under mechanical and/or thermal loads［J］.Mechanics of Materials，1995，19：281-92.

［10］LIANG C，ROGERS C A.The multi-dimensional constitutive relations of shape memory alloys［J］.Journal of Engineering Mathematics，1992，26：429-443.

［11］莊茁，張帆，岑松，等.ABAQUS非線性有限元分析與實例［M］.北京：科學出版社，2005.

［12］LAGOUDAS D C，BO Z，QIDWAI M A.A unified thermodynamic constitutive model for SMA and finite element analysis of active metal matrix composite［J］.Mechanics of Composite Materials ＆ Structures，1996，3：153-79.