對含FACTS元件的電力系統潮流的計算與控制

許景毓

(華北電力大學電氣與電子工程學院,北京 102206)

對含FACTS元件的電力系統潮流的計算與控制

許景毓

(華北電力大學電氣與電子工程學院,北京 102206)

社會在發展,科技在進步,與每一個人的生活都息息相關的電力這一行業也在突飛猛進的發展。伴隨著現在快節奏生活對電力各方面的需求越來越大,柔性交流輸電技術正在慢慢地占據主流。柔性交流輸電裝置能對電力系統進行靈活、快速的控制,提高電網的輸電能力,增強系統的經濟性、可靠性和安全性,使電力系統正朝著較高可控性的方向發展。建立相應的、正確且合適的穩態潮流計算模型是對各種FACTS裝置研究和控制的基礎。本文在這種情況下,構建模型對含FACTS元件的電力系統潮流的計算與控制。

FACTS元件 電力系統潮流 計算

1 前言

全球的電力事故時有發生,因電力事故造成的損失難以估計,如果想要把一損失降到最低,就必須在安全用電的基礎上將這一過程中出現的問題各個擊破！國際上現在已經把靈活交流輸電系統(FACTS)作為一個重要課題在研究,其通過先進的科學手段,利用數碼信息與機械的相互交叉滲透,巧妙的對電力系統運行過程中的各個方面和環節進行有效的監控,不但能有效的防止各種電力事故的發生,減少因電力事故而造成的損失,而且使輸電的效率有了一個質和量的飛躍,因此找到一個能正確有效的使用前面元件的途徑在電力系統潮流計算中起著舉足輕重的作用。

2 對FACTS元件穩態潮流模型的構建

2.1 構建原則

一個FACTS元件的穩態潮流計算模型和算法應該具有良好的有效性,這具體表現在以下幾個方面:(1)模型是否直觀且物理概念清晰,能否準確反映FACTS元件對系統的影響；(2)模型是否精確；(3)采用該模型和算法進行潮流計算時的速度和收斂性能；(4)模型的通用性,即是否適合多種FACTS元件的建模；(5)是否容易嵌入已有的潮流計算程序中,易于與傳統的潮流計算程序相結合而不必做較大的修改,便于編程實現。

模型可以有所不同,這個要特殊情況特殊對待,一個模型不可能適用于全部,所以這個沒有作為一個硬性要求。

2.2 UPFC等效電路

UPFC的基本工作原理由含中間直流環節的兩個背靠背的換流器組成。

根據圖1UPFC的原理結構和功能,UPFC可以用圖所示的等值電路來表示。該等值電路適用于UPFC的串并聯支路中耦合變壓器的漏抗和電阻相對于輸電線路的阻抗較小的情況。通常情況下UPFC的損耗相對較小可以忽略,UPFC的串聯部分被等效為一個理想電壓源VS,UPFC的并聯部分被等效為一個理想電流源Ish。理想電壓源的幅值VS和相角θS可以控制,受UPFC的容量限制和系統安全穩定的考慮,理想電壓源的幅值VS和相角θS運行在以下約束限制的范圍內:VSmin≤VS≤VSmax,0≤θS≤2π。理想電流源Ish(Ish≤IN

sh,是換流器1的電流容量)也可控。這里的Ymk=Gmk+jBmk是節點m和k之間的線路導納。在圖中Ish被分解為兩個分量:一個是與UPFC并聯接入處的節點電壓Vm同相的分量IT,由換流器2與系統交換的有功功率和UPFC的損耗確定；另一個是與Vm正交的分量Iq,由它提供無功功率維持所在節點的電壓水平。對無功分量Iq,我們定義:當Iq超前Vm90°時為正,滯后Vm90°時為負。對有功分量IT,我們定義:當IT與Vm同相時為正,與Vm反相時為負。

忽略UPFC的損耗時,換流器1從系統吸收的有功功率等于換流器2注入線路的有功功率,即滿足以下約束條件:

圖1 UPFC的等效電路圖

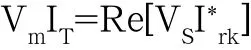
此約束表示UPFC既不吸收也不發出有功功率,所以在節點r處流經線路的有功功率Prk等于Pmk:Pmk=Prk

設線路m－k上的潮流Pkm+jQkm被UPFC控制等于給定值PC+jQC。

于是含UPFC的線路有功、無功潮流如下:

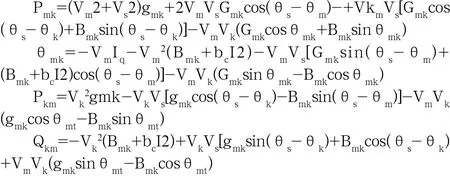
3 對FACTS元件穩態潮流模型的計算與控制

當UPFC連接在線路m-k上節點m處時,由UPFC的功率注入模型,含UPFC的電網潮流方程可列寫如下:

n是系統總的節點數。PGi、QGi是節點i的電源輸入功率,PLi、QLi是節點i的負荷需求功率。這里,

Yij=Gij+jBij是系統節點導納矩陣的相應元素。因此修正方程式可以寫作:

不含UPFC時常規快速解偶法的修正方程式與這個公式是一樣的,系數矩陣B′和B′′與常規快速解偶法中的系數矩陣也是一樣的,因此UPFC的等效節點附加注入功率只是系統節點狀態變量(節點電壓幅值和相角)和UPFC的控制變量VS、θS的函數。我門只要增加相應的潮流方程和兩個狀態變量便能得出含UPFC的電網潮流分布的答案。因為引入0～2π變化的控制變量θS作為新增加的狀態變量而引起潮流計算的準確性會降低,所以我們用PK(i≠j)和QK(i≠j)著兩個變量來計算。因為知道K(i≠j)P和QK(i≠j)的值,所以我們一般情況下經過計算就可以得到UPFC的控制參數VS和θS,進而可以求出UPFC的其他等效節點附加注入功率PM(i≠j)、QM(i≠j)的值。其中:

因此,給定PK(i≠j)、QK(i≠j)和系統狀態變量(節點電壓幅值和相角)的初值,可以得到UPFC的其他等效節點附加注入功率和控制參數VS、θS的初值,通過式表示的主迭代過程可以求出系統節點狀態變量的修正量,從而得到系統節點狀態變量的新值,將系統節點狀態變量的新值代入式表示的子迭代過程,又可以求得PK(i≠j)和QK(i≠j)的新值。如此交替迭代。

4 結語

想要更好的控制電力為人類服務就必須掌握有效的控制電力的方法,而靈活交流輸電系統恰好是一個方便有效的方法,所以準確的掌握這一方法尤為重要,潮流計算作為掌握這一方法的基本途徑是重中之重,希望上面公式的計算可以給廣大電力研究工作者提供一些幫助,更希望因為這個公式計算而找到更加有效的控制電力的新方法。

[1]丁明,查軼美,李生虎.包含統一潮流控制器的概率潮流研究[J].合肥工業大學學報(自然科學版),2013(1).

[2]丁明,李生虎,黃凱.基于蒙特卡羅模擬的概率潮流計算[J].電網技術,2001(11).

[3]吳捷,王建.基于UPFC的靈活交流輸電潮流控制計算[J].電力系統自動化,2001(8).

[4]王仲鴻,沈斐,吳鐵錚.FACTS技術研究現狀及其在中國的應用與發展[J].電力系統自動化,2010(23).

[5]劉文華,梁旭,姜齊榮,羅承廉,劉遵義.采用GTO逆變器的±20Mvar STATCOM[J].電力系統自動化,2000(23).

[6]陳菊明,梅生偉,劉鋒.多機系統TCSC多目標H_∞控制器設計[J].電力系統自動化,2000(21).