無定向導線在礦山測量工作中的可行性分析

王躍剛

(云南錫業集團有限責任公司大屯錫礦,云南個舊 661021)

無定向導線在礦山測量工作中的可行性分析

王躍剛

(云南錫業集團有限責任公司大屯錫礦,云南個舊 661021)

本文就大屯錫礦在老區,用無定向導線測量方法,解決采區坑內導線延伸問題,對無定向導線施測精度、可靠性進行分析論證。

無定向導線 精度 限差

1 引言

由于礦山井下開采和地壓活動或其它各種原因，使布設在巷道頂板上的一些測量控制點遭到破壞或位移，導致控制點間不通視，在沒有陀螺經緯儀的情況下，無法在已知控制點上繼續延伸導線。要想重新引測導線，測量野外工作量大，有的地方甚至無法進行引測，給測量工作帶來了許多困難，影響礦井的日常生產。為此，如何利用原有不通視的控制導線點，進行該測區的導線延伸，是本文研究的主要課題。

2 無定向導線測量方法及原理

2.1 定義

無定向導線：在孤立且不通視的兩個已知控制點間，通過連測一段導線(測水平角，丈量邊長)，將兩點連接起來，導線無方向(無知已方位角即已知邊)，但是可以利用這兩個已知控制點，通過內業技術手段計算求得各導線點的坐標。

2.2 測量方法及計算原理

2.2.1 外業測量

外業測量工作與常規導線測量一樣，它包括：選點、埋點、測角、量邊等測量工作內容，所不同的是：用經緯儀測水平角時，起始的第一站是在未知點上安置經緯儀或全站儀，后視目標為已知點，前視為無定向導線埋設的導線點，依次分測站測量水平角到另一已知點上。而量邊方法是從后視目標的已知點開始依次分段丈量到另一已知點上，由所測水平角和邊長連接后，即可構成一條無定向導線。

2.2.2 內業計算

對于任意一條無定向單導線，如圖1：

A和B為兩端已知控制點，t為無定向導線點數，β(i=1～t)為觀測左角，S(i=1～t+1)為觀測邊長。計算時，先假定起始邊A1的方位角為αA1，按導線的觀測水平角βi，推算各邊的假定方位角。再按導線各邊的觀測邊長Si及假定方位角αA1，推算各邊的假定坐標增量及各點的假定坐標，直至B點的假定坐標為(X＇B，Y＇B)。由A、B兩點的假定坐標，計算閉合邊AB的假定邊長和假定方位角：

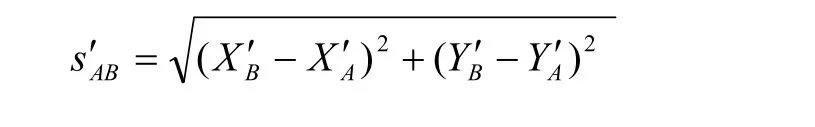
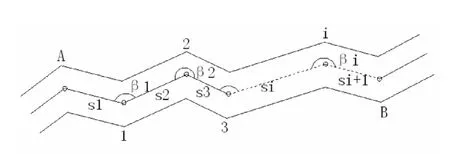
圖1

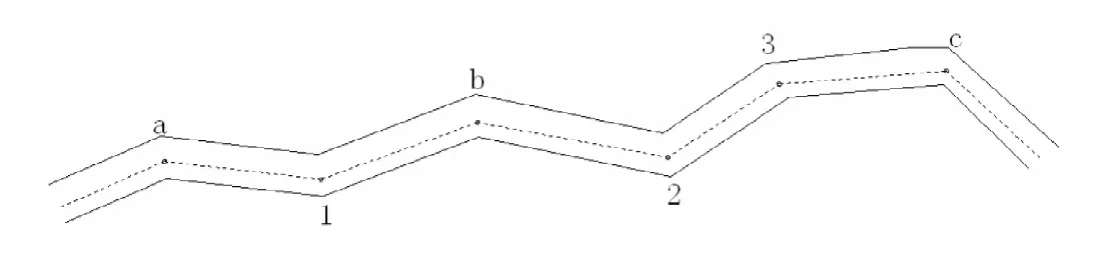
圖2

根據A和B兩點的已知坐標，可以計算閉合邊AB的已知邊長SAB和已知方位角αAB，根據已知、假閉合邊長和方位角，計算已知、假閉合邊長度比R和方位角差△α：

然后按R及△α改正導線各邊的邊長和方位角：

用改正后的方位角及邊長計算各邊的坐標增量，最后推算各點的坐標。

3 無定向導線的精度分析

由于無定向導線的精度是受原導線精度制約，所以僅依現連接導線的測量精度是保證不了工程需要的。因為無論現連接導線的測量精度多么高，其導線的有效精度也不會高于原導線的精度。我們設原導線誤差為md1，無定向導線連測誤差為md2，則無定向導線的有效精度可根據下式計算：

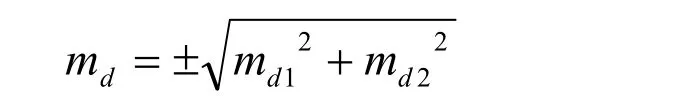
式中：md1、md2分別為原導線與現連接導線的精度。

例如本實例是在原3"導線1點與314點之間，布設了5"無定向導線，則該導線的有效精度為：

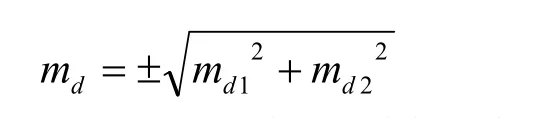
在實際工作中應以其有效精度作為衡量無定向導線精度的一項測量技術指標。

4 無定向導線的可靠性檢查

測量規范中規定，在井下導線測量前首先要進行起始點位的檢查，符合要求后再進行導線測量，對于無定向導線中的控制點，如何確保其絕對可靠，只有且必須進行測量檢查。其方法是采用原有至少3個控制點進行連測檢查。可通過測量計算相互兩控制點間的距離差(即檢查其縱向是否移動)進行檢查；測量點的位移多半是因巷道的壓力隨巷道作橫向移動造成的且影響很大，所以對垂直于兩控制點連線方向上點移動的檢查尤其重要。在內業計算時首先對其控制點間進行縱向(邊長)與橫向(方位)的檢查符合要求后方可使用該無定向導線。否則應進一步采取其它措施。下面以三點控制無定向導線的測量方法為例。分述其控制點間的縱橫向檢查并給出限差公式 。

4.1 控制點縱向移動的檢查及限差

如圖2所示：

a、b、c為原導線的殘存點，作為現無定向導線的控制點，其余(圖中 1、2、3點)為新設點，外業工作只在a至c點間按要求進行測量連接無定向導線，內業計算時首先按假定坐標及方位角計算連接導線。然后反算該導線中控點間的距離S＇ab、S＇bc，假定方位α＇ab、α＇bc和原導線點間距離Sab、Sbc及方位αab、αbc，最后求其差值：△Sab=Sabc-S＇ab，△Sbc=Sbc-S＇bc。限差可借用兩井定向中兩垂線間距離容許差值公式計算得出，即：

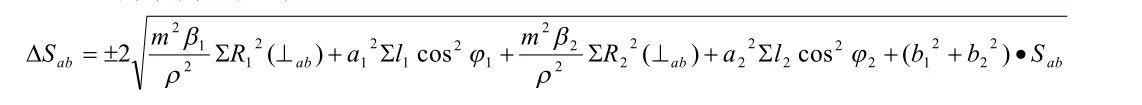
式中：

R1(⊥ab)----原導線a、b間各點到ab連線的垂直距離。

R2(⊥ab)----現連接導線a、b間各點到ab連線的垂直距離。

mβ----測角中誤差

l----各導線邊的長度

a----量邊偶然誤差系數

b----量邊系統誤差系數

φ----各導線邊與ab連線的夾角

若現連接導線與原導線施測精度相同，且測點位置及其它條件大體相似，則上式可簡化為：

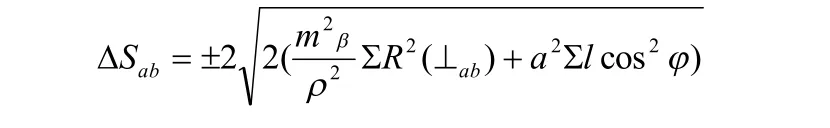
同理，△Sbc的限差與此類似 。在實際工作中，若 a、b、c三點接近一直線，即直伸形導線，此時，該項限差可以適當放寬。另外，此項限差也可根據導線全長相對閉合差簡明地估算。如原導線為 3"級導線現連接導線為5"級導線。則 △Sab允可采用下面公式進行計算：

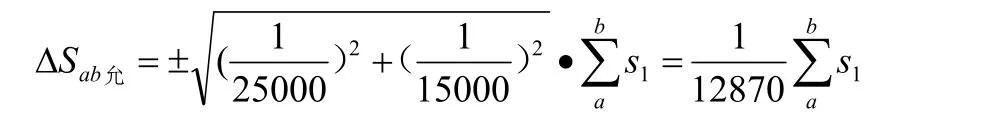
以上公式為控制點縱向移動的測量限差檢查確定方法。當所求△Sab允小于連測導線閉合差，則控制點的縱向位移對導線精度在允許范圍內。

4.2 控制點橫向移動的檢查及限差

根據己反算得出的αab、αbc、α＇ab、α＇bc將其轉化為水平角β，即βabc=αbc-αba，β＇abc=α＇bc-α＇ba。差值△β=βabc-β＇abc，限差△β允的確定與上述類似，可用誤差預計的方法求得其限差，具體方法是以b點為原點，先分別計算終點a在垂直于ab方向上的中誤差m⊥ab，點c在垂直于bc方向上的中誤差m⊥bc，它們與其相應邊長之比相的中誤差為再求出水平角β 的限差△β 。abc允

式中m⊥ab、m⊥bc的求取根據以下兩種情況而定：

第一種：原導線與現連接導線施測精度不同。

如：

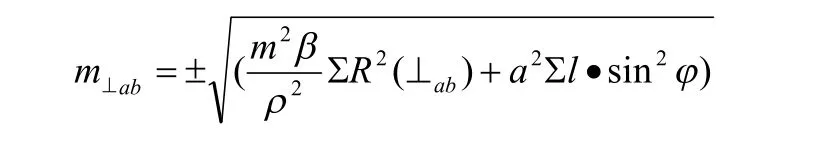
式中 mβ----測角中誤差

R(⊥ab)----連測點到ab連線的垂直距離

a----量邊偶然誤差系數

l----各導線邊的長度

φ----各導線邊與ab連線的夾角

第二種：原導線與現連接導線施測精度相同時可按復測支導線預計終點平均值中誤差 m⊥ab、m⊥bc，為方便計算，可認為這兩遍導線測站數相等(取平均)。

則：

當△β允小于連測導線測角中誤差，則控制點的橫向位移對導線精度影響在允許范圍內。

在實際工作中應根據需要，可適當多連接一些原導線點，這將有助于對控制點是否移動作可靠的檢核，當控制點的縱向位移限差和橫向位移限差都在允許的范圍內時，說明控制點可靠，可以用于導線連測的起始控制點，反之，則不可用。

5 結語

本文闡述了無定向導線的測量計算方法，分析了無定向導線的有效精度及限差的確定。總結出無定向導線精度受原導線精度的制約，無論連接導線的測量精度多高，其導線的有效精度也不會高于原導線的精度。

[1]《礦山測量學》(上).煤炭工業出版社,1997年.

[2]《礦山測量技術規定》.云錫有限責任公司,2009年.

[3]《誤差理論及應用》.昆明冶金工業學校,1986年.