有色噪聲對動態尋北的影響

蔣慶仙，白云超，王成賓

(西安測繪研究所，陜西西安710054)

一、引 言

陀螺尋北儀是一種采用陀螺儀作為角速率傳感器快速精確測定真北方位的儀器。隨著慣性技術、電子技術和計算機等技術的進步，陀螺尋北儀在車輛導航定位、海洋勘探、石油鉆井、隧道開鑿等領域均得到了日漸廣泛的應用。根據采樣和解算方式的不同，陀螺尋北儀有多種尋北方法。近年來興起了動態旋轉調制尋北法，在尋北過程中，慣性測量單元IMU(由陀螺儀和加速度計組成)繞其垂直中心軸連續轉動，通過采樣陀螺的輸出信號解算出陀螺敏感軸的初始方位角［1-5］。其優點是通過連續轉動使陀螺的常值漂移、隨機漂移受到周期性調制，通過積分得到消除，因而可顯著提高尋北精度。

在動態定位測量中，觀測誤差往往不屬于高斯白噪聲，而是具有一定時空相關性的有色噪聲。有色噪聲可看作是某一線性系統在白噪聲驅動下的響應，它的存在嚴重影響著動態濾波的精度和可靠性，有必要在數據處理中加入有色噪聲的檢驗和建模，以消除或減弱有色噪聲對參數估計的影響。現已形成了多種減弱和消除有色噪聲影響的方法，如附加有色參數濾波法、相鄰觀測值組差法、基于濾波殘差建模法、自適應濾波和自適應抗差濾波［6-8］。在數據處理中常利用白噪聲的定義與統計特性判斷觀測噪聲是屬于白噪聲還是有色噪聲。目前對有色噪聲建模比較麻煩，常用的建模方法一般分為相關函數法和時間序列分析法，如AR模型、指數相關函數和高斯相關函數［9-10］。通過對有色噪聲建模、擬合、預報，以及對觀測值進行誤差修正，使觀測值中僅留下白噪聲或近似于白噪聲，從而減弱有色噪聲對參數估計的影響。

為了分析有色噪聲對動態尋北中方位角估值的影響，本文在一階自回歸AR模型的假設下推導了有色噪聲對參數最小二乘估值的影響函數，分析了其影響性質。利用觀測殘差建立了有色噪聲的一階AR模型，并對有色噪聲進行了擬合和預報［11］。為了削弱陀螺信號中異常噪聲對尋北精度的影響，對陀螺信號進行了抗差估計以控制粗差的影響。計算結果表明，當陀螺信號中包含有色噪聲時，采用一階AR模型對有色噪聲進行擬合和預報，能夠有效削弱有色噪聲的影響。采用一次啟動漂移穩定性為0.03°/h的動調陀螺，在4 min之內系統尋北精度小于0.6'，遠高于不考慮有色噪聲影響得到的精度，極大地提高了系統的性能。

二、有色噪聲對參數最小二乘估值的影響

設有觀測序列 L1，L2，…，Ln，觀測方程為

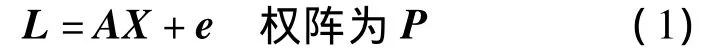
式中，X為參數向量;A為設計矩陣;e為真誤差向量，其協方差矩陣為Σk。

當e為高斯白噪聲序列時，參數的最小二乘(LS)解為［12］

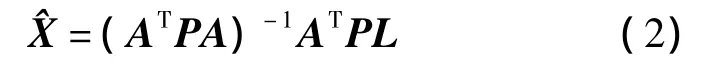
當e為有色噪聲時，采用時間序列分析法描述有色噪聲，即把平穩的有色噪聲看做是由各時刻相關序列和各時刻出現的白噪聲所組成。將tk時刻的有色噪聲ek表示為［13］

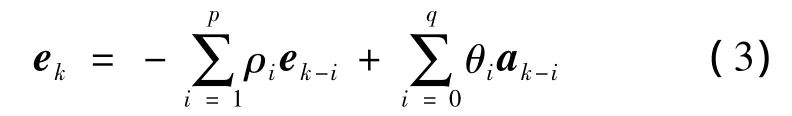
式中，ρi＜1(i=1，2，…，p)為自回歸參數;θi＜1(i=1，2，…，q)為滑動平均參數;ak為白噪聲，服從分布N(0，)。

式(3)稱為自回歸滑動平均ARMA(p，q)模型。模型前半部分稱為自回歸模型AR(p)，后半部分稱為滑動平均模型MA(q)。

設有色噪聲模型為一階AR模型，k時刻的觀測誤差向量表示為

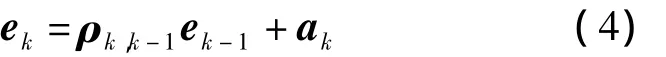
式中，ek-1為 k-1 歷元的觀測誤差;ρk，k-1為相關系數矩陣;ak為高斯白噪聲。將Lk修正為

則近似有

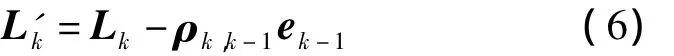
式中，L'k為經過有色噪聲改正后的觀測值。顧及式(2)可得參數最小二乘解為［9，11］

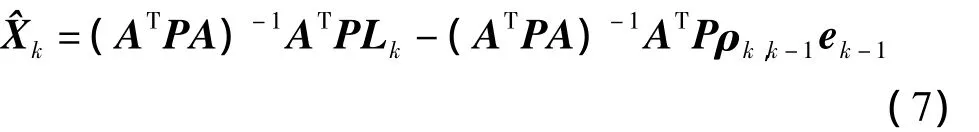
因而，有色觀測噪聲對參數解向量的影響函數(influence function，IF)為

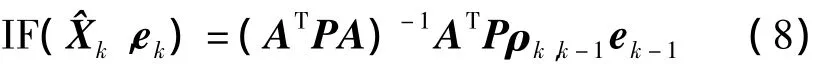
由式(8)可見，純有色噪聲對參數最小二乘估計解的影響主要與觀測誤差、相關系數及設計矩陣有關。當加大觀測的采樣間隔時，其相關系數ρk，k-1必然減小，前面歷元的觀測誤差對本歷元參數估計的附加影響就小。當前一歷元的觀測精度很高，即ek-1很小時，有色噪聲對參數估計的影響也將減小。

三、有色噪聲的擬合與預報

1.有色噪聲的擬合

當觀測值中存在有色噪聲時，利用觀測殘差在一階自回歸模型的基礎上建立有色噪聲模型。將k時刻的觀測殘差表示為

對于觀測殘差序列，有誤差方程

當誤差Δk服從正態分布時，有色噪聲模型參數的最小二乘估值為

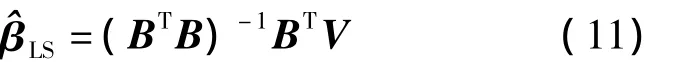
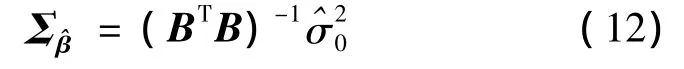
2.有色噪聲的預報

有色噪聲改進后，重寫誤差方程如下

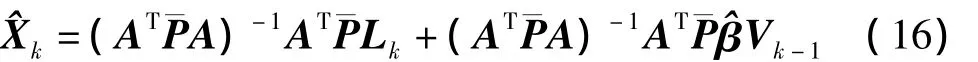
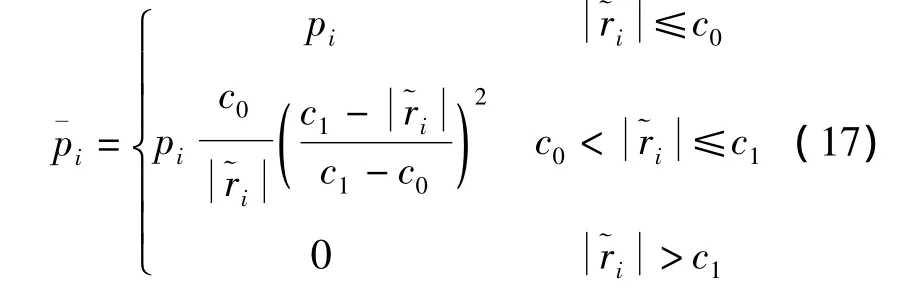
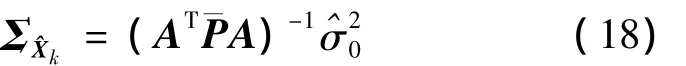
式(16)的解算一般采用迭代法，第k+1步的迭代解為

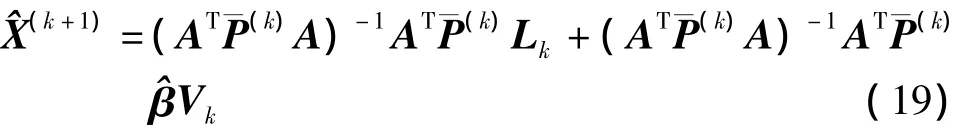
四、計算與分析

試驗數據來自動調陀螺尋北儀，進行了7個測回的尋北試驗。動調陀螺的一次啟動漂移穩定性為0.03°/h。轉臺的轉速設定為5 r/min，分別采集陀螺儀x、y軸的輸出信號，采樣率為25 kHz。采用高精度的鎖相穩速控制電路使轉臺速率的相對穩定度達到10-4，DSP+FPGA構成了數據的高速采集與解算單元。

采用第1個測回的數據計算狀態參數的初值，

在基于觀測殘差序列使用式(11)或式(13)獲得AR模型的參數后，有色噪聲的預報值可表達為［11］采用第2—7個測回的數據計算參數的估值并評定尋北精度。對測試數據采用以下5個方案處理，測值的權反映了每個測回的估值對本方案中方位角估值的貢獻。抗差估計中迭代收斂的條件為，等價權函數的臨界值c0、c1分別取為1.5和5。由于還沒有得到方位角的實際值，計算中采用觀測值的中誤差考核尋北精度。表1給出各個方案中方位角的計算結果。

方案1:不考慮有色噪聲影響的最小二乘估計;方案2:不考慮有色噪聲影響的抗差估計;

方案3:對有色噪聲進行最小二乘擬合的最小二乘估計;

方案4:對有色噪聲進行最小二乘擬合的抗差估計。

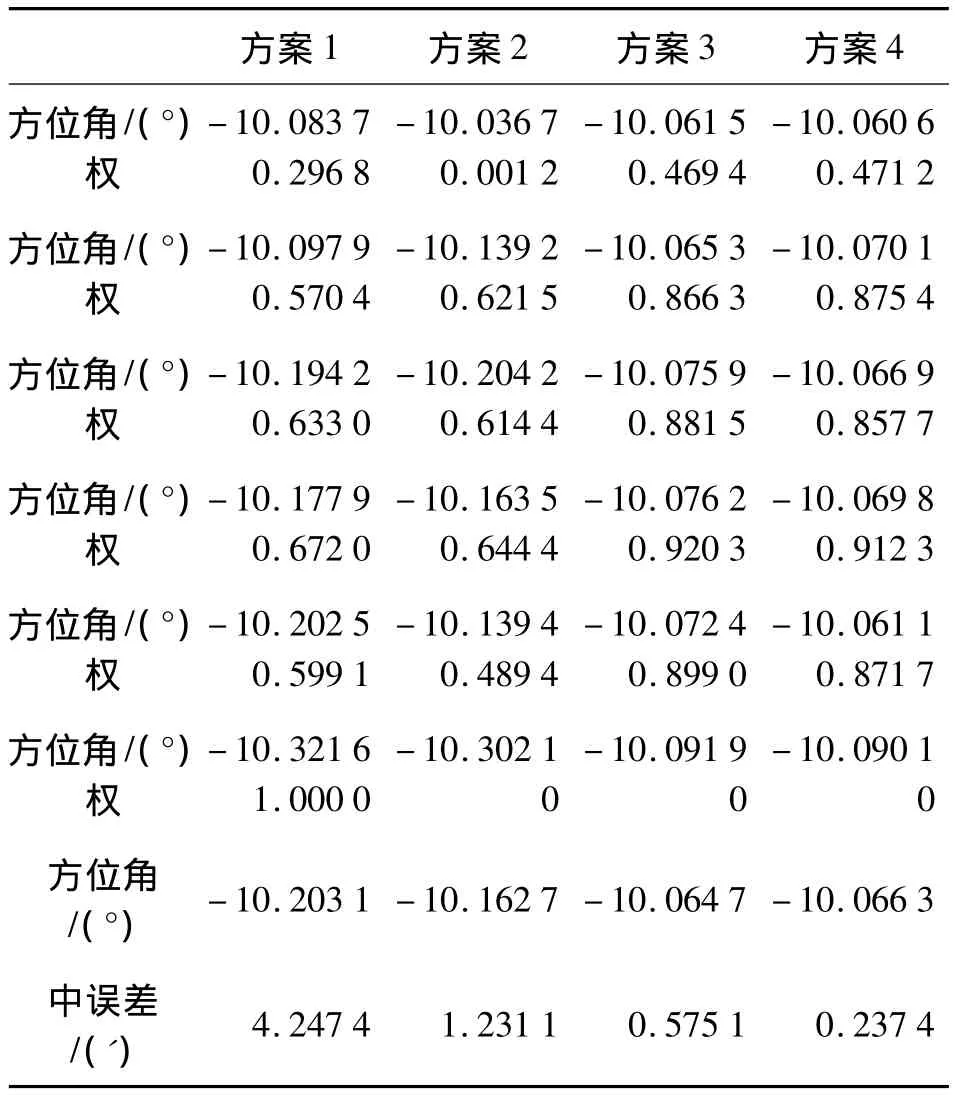
表1 尋北結果

為了直觀顯示有色噪聲擬合的效果，由圖1、圖2分別給出觀測值的原始殘差和有色噪聲擬合后的觀測殘差。由此可以看出原始殘差的幅值為0.2°/h，而經過有色噪聲擬合后的觀測殘差為0.1°/h。

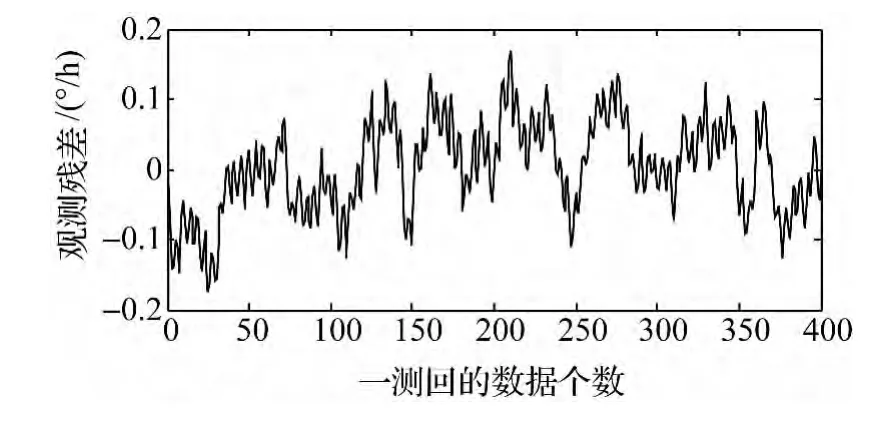
圖1 原始殘差

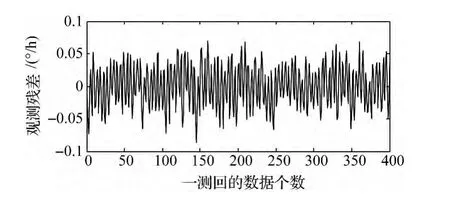
圖2 有色噪聲擬合后的殘差

五、結 論

分析上述結果，可得如下結論:

1)陀螺儀信號中包含有色噪聲時，動態尋北的精度和可靠性將受到嚴重的影響(見方案1的尋北結果)。

2)抗差估計能夠削弱信號中存在的異常干擾的影響，并且可以將異常干擾剔除而不影響其余有用信號。算例中第6測回計算得到的方位角偏離了方位角的最終估值，但采用抗差估計時給予其零權處理，從而減弱了載體擾動對方位角估值的影響。

3)采用一階自回歸模型對有色噪聲進行擬合和預報，能夠有效削弱有色噪聲的影響，極大地提高了系統的尋北精度(見方案3、方案4的尋北結果)。

4)最小二乘估計不具有抗差性，其控制粗差影響的能力要低于抗差估計。在采用最小二乘估計對有色噪聲進行擬合和預報后，再進行抗差估計，獲得了明顯優于最小二乘估計的結果。

綜上所述，有色噪聲對參數估計的影響不容忽視，在動態尋北測量數據處理中，應充分考慮有色觀測噪聲的影響。當陀螺儀信號中包含有色噪聲和異常干擾時，采用最小二乘估計對有色噪聲進行擬合和預報，在此基礎上進行抗差估計能夠有效控制載體擾動和有色噪聲兩者的共同影響。

［1］KIM S J，LEE S S，KWON Y S.Dynamic North-finding Scheme Based on a Fiber Optic Gyroscope［C］∥Proceeding of SPIE.Orlando:SPIE，1997:126-136.

［2］KIM I S.KIM Y，Matisov A，et al.Dynamic Scheme North Finder Using a Fiber Optic Gyroscope［C］∥Proceeding of SPIE.Beijing:SPIE，1996:228-236.

［3］鄒向陽，孫謙，陳家斌，等.連續旋轉式尋北儀的尋北算法及信號處理［J］.北京理工大學學報，2004，24(9):804-807.

［4］徐建華，謝玲，高亞楠，等.旋轉調制式尋北儀濾波技術研究［J］.北京理工大學學報，2005，25(8):718-721.

［5］張思將，秦石喬，王省書，等.連續旋轉式激光陀螺尋北儀研究［J］.航空兵器，2006(1):12-15.

［6］趙長勝.有色噪聲濾波理論與算法［M］.北京:測繪出版社，2011.

［7］崔先強.動態導航有色噪聲的影響與控制［D］.鄭州:信息工程大學，2003.

［8］崔先強，楊元喜，高為廣.多種有色噪聲自適應濾波算法的比較［J］.武漢大學學報:信息科學版，2006，31(8):731-735.

［9］楊元喜，崔先強.動態定位有色噪聲影響函數——以一階 AR 模型為例［J］.測繪學報，2003，32(1):6-10.

［10］吳富梅，楊元喜.顧及有色噪聲的光纖陀螺信號的抗差譜分析［J］.測繪科學與工程，2006，26(3):50-53.

［11］楊元喜.自適應動態導航定位［M］.北京:測繪出版社，2006，178-185.

［12］楊元喜.抗差估計理論及其應用［M］.北京:八一出版社，1993.

［13］劉永紅，范躍祖.激光陀螺漂移的非平穩隨機信號建模［J］.戰術導彈控制技術，2004，46(3):99-102.

［14］YANG Y.Robust Estimation of Geodetic Datum Transformation ［J］.Journal of Geodesy，1999，73(5):268-274.

［15］YANG Y，CHENG M K，SHUM CK，et al.Robust Estimation of Systematic Errors of Satellite Laser Range［J］.Journal of Geodesy，1999，73(7):345-349.