重力場擾動位泰勒展開式低階項應用研究
曹金國,王建斌,戴山嶺
(96633部隊,北京100096)
一、引 言
高程異常是似大地水準面和參考橢球面之間的差距,似大地水準面相對于參考橢球面的傾斜狀況可以采用垂線偏差來衡量。垂線偏差通常采用天文測量和大地測量相結合的方法確定,或通過重力場模型獲取。其中,天文測量受天氣制約明顯,而重力場模型對低頻長波擾動影響表征較好,對局部短波高頻擾動影響反應較差。特殊情況下,需要一定精度垂線偏差分量而天文測量又無法實施時,就需要其他手段來保障。多年來,筆者在局部區域內實測了一定數量的高程異常點,而通過這些高程異常點能否確定該區域內任意位置滿足一定精度的垂線偏差,下面就這一問題進行探討。
二、擾動位局部平面展開式低階項的物理意義
眾所周知,垂線偏差代表了似大地水準面的傾斜,垂線偏差分量(ξ,η)和擾動位T的關系可以簡單地表示為
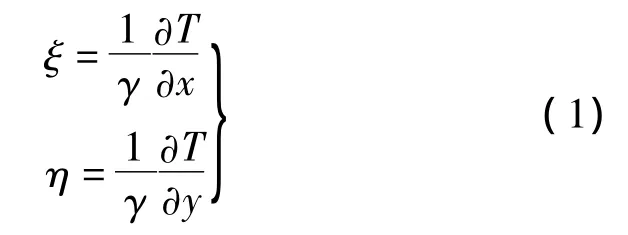
式中,γ為正常重力值。
考慮到一定范圍內似大地水準面的變化比較平緩,可將擾動位T看做是平面坐標(x,y)的函數,此時,可將擾動位展開為x和y的函數,即
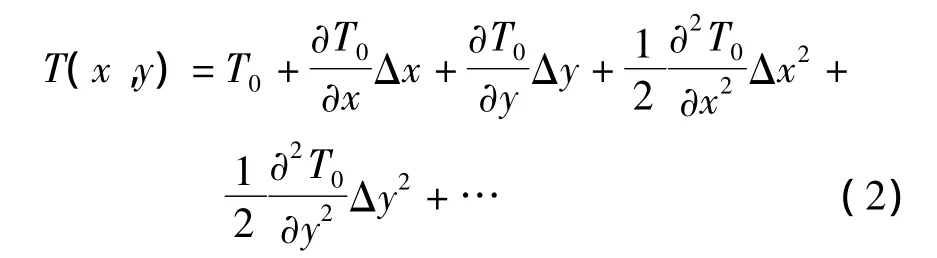
式中,T0為參考點處(重心)的擾動位。參考點處擾動位的偏導數與垂線偏差,以及垂線偏差變化率的關系為
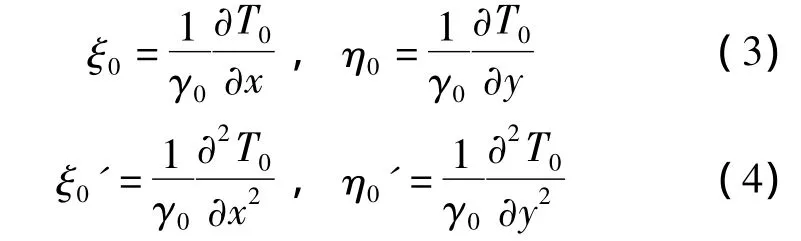
式中,γ0為正常重力。將式(3)和式(4)代入式(2)后可得
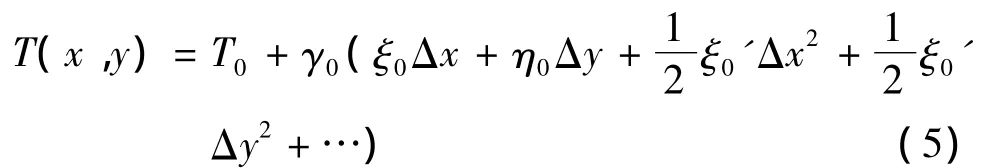
將式(5)代入到布隆斯公式可得

由正常重力的計算公式可知,相隔數十千米的兩點,正常重力的變化可忽略不計,即可取γ=γ0,則可得到和高程異常ζ與垂線偏差(ξ、η)的關系式,即
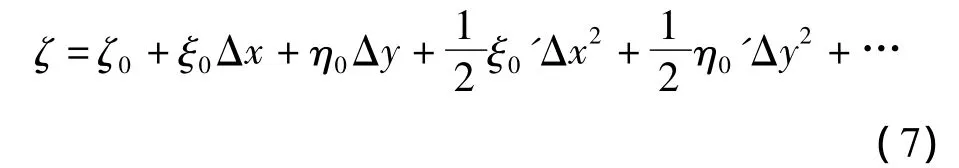
式中,ζ0為參考點的高程異常;(ξ0、η0)為參考點的垂線偏差分量;二次項的系數是垂線偏差的變化率。由此可見,式(7)是一個典型的多次曲面函數,因此可以將主要的低階項采用二次曲面函數進行擬合,即
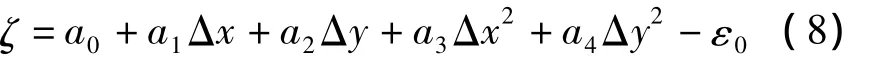
正因為二次曲面函數具有高程異常和垂線偏差聯系的物理意義,因此可以通過高程異常擬合垂線偏差。
三、利用二次曲面擬合垂線偏差的方法
假如區域內有n個已知高程異常值的點位S(x,y,ζ),根據式(8)可以列出高程異常的誤差方程
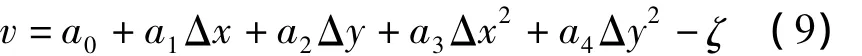
當n=3時,可以直接采用一次項,直接解算方程便會得到重心處的垂線偏差分量;當n=5時,可以采用二次項,直接解算出6個系數 a0、a1、a2、a3、a4、a5;當n>5時,需要采用最小二乘原理進行平差,此時若記

則可得到多項式擬合的各系數
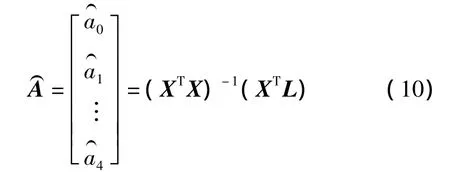
在得到 a0、a1、a2、a3、a4的基礎上,區域內任意點的垂線偏差則是

四、擬合結果分析
采用東南部3個測區不同數量的高程異常值對垂線偏差進行了擬合,3個測區的范圍分別為25 km×40 km、26 km ×25 km、25 km ×10 km,其高程異常值均采用GPS和三等電磁波測距高程導線測量所得。由于測區已知高程異常點數量較少,均為4個點,因此這3個測區僅能夠擬合出重心處的垂線偏差分量,對擬合結果與CGCS2000模型的計算結果進行了比較,結果見表1。

表1 3個測區垂線偏差分量(ξ、η)擬合結果(″)
為了驗證測區內任意位置垂線偏差的擬合情況,測區3中采用CGCS2000計算出兩個點的高程異常作為已知點高程異常,這樣便可以求出垂線偏差在兩個方向的變化率。采用以上模型求出測區范圍內1'×1'格網交叉點處共計78個點的垂線偏差,然后采用CGCS2000模型計算出這78個點的垂線偏差分量,將CGCS2000模型的計算結果作為已知值,對擬合的垂線偏差兩個分量分別進行了精度統計,擬合精度m的計算公式為

式中,Δ為擬合值與CGCS2000計算值之差。結果見表2。
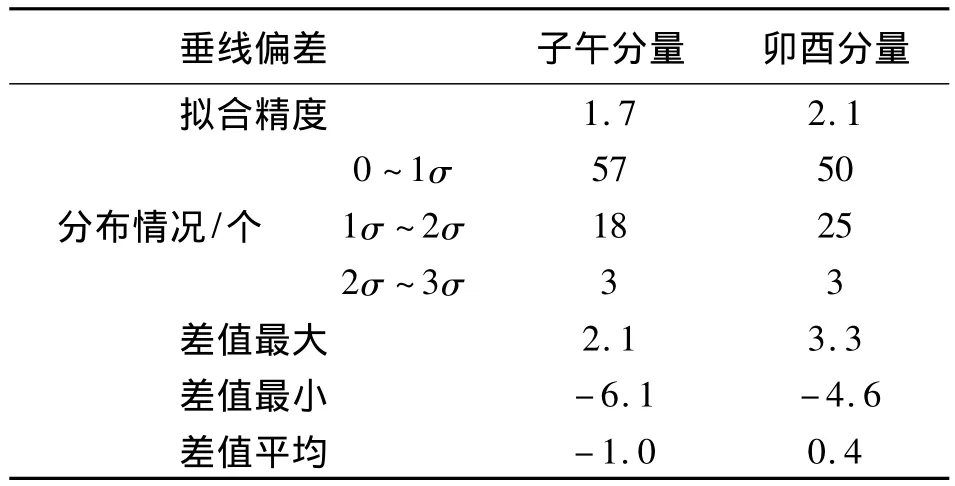
表2 測區3內垂線偏差分量擬合結果分布情況(″)
通過表1和表2的擬合結果可以看出,采用高程異常可以擬合出滿足一定精度要求的垂線偏差分量。
五、垂線偏差擬合時的高程異常精度要求
由于高程點的精度通常采用每千米高差中數偶然中誤差mΔh來衡量,忽略大地高的測量誤差,因此高程點的高程異常精度mh可以根據路線長度s按照以下公式計算得出

為了簡便起見,設Δx=Δy,并且忽略高階項的影響,可以得到局部區域內高程異常與垂線偏差的精度關系,即
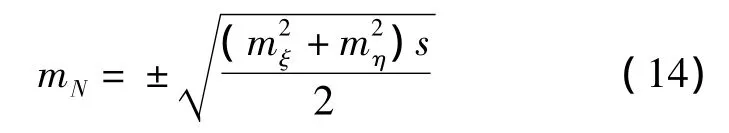
取兩個分量的誤差精度相同,即mξ=mη=m,可以概略地確定高程異常和垂線偏差的精度關系

將式(13)代入式(15),并且取每千米高差中數偶然中誤差mΔh=10 mm代入計算,則可得到m大約在2.1″左右。考慮到模型的誤差,可以滿足垂線偏差分量2.5″的精度要求,從另一個方面證明了該方法的可行性。
六、結束語
本文分析了擾動位局部平面展開式低階項的物理意義,并根據其物理意義采用相應的二次曲面函數進行了垂線偏差分量的擬合試驗。試驗結果表明,該方法滿足一定精度要求,可以作為特殊情況下垂線偏差獲取的途徑。另外,在測區范圍的大小及已知點的分布情況對精度影響方面,還有待深入研究。
[1]陸仲連.地球重力場理論與方法[M].北京:解放軍出版社,1996.
[2]王新洲,陶本藻,邱衛寧,等.高等測量平差[M].北京:測繪出版社,2006.
[3]隋立芬,宋力杰,柴洪洲,等.誤差理論與測量平差基礎[M].北京:測繪出版社,2010.

