優化學生規律探索的思維活動過程

高飛

蘇教版數學教材將“商不變的規律”正式編在四年級下冊“用計算器探索規律”單元，以期在提高學生用計算器計算較大數的乘除法技能的基礎上，探索發現乘、除運算中所包含的“積的變化規律”和“商不變的規律”，并初步應用所學規律解決一些計算問題，感受及體驗規律學習的實際價值。但談到用計算器探索“商不變的規律”的教學素材時（如圖1），

不難發現，例題編排意圖是憑借8400÷40=210，提出“把被除數和除數同時乘或除以一個數（0除外）”的探究要求，從而使學生通過列舉試算，初步發現“在除法中，被除數和除數同時乘或除以一個數（0除外），商不變”的現象并以此作為猜想，進而鼓勵學生繼續舉例進行計算驗證，最后歸納概括出商不變的規律。主要過程性目標是使學生經歷規律探索的一般過程，積累學科探究活動經驗。可是，站在學生的視角，探究需求在哪里？為什么要把被除數和除數同時乘或除以一個數，而不是同時加或減去一個數？為什么要強調“同時”？這里“同時”又作何理解？為什么必須是乘或除以同一個數？不同的數行不行？為什么要把0除外？等等。其實，對這些問題的質疑和探索，正是學生經歷“商不變的規律”萌發、生長與形成的過程所必須思考及解決的問題。由此可見，學習商不變的規律的“重頭戲”不是發現商不變的現象，而是引導學生執“果”索“因”地探究思考“商不變現象客觀存在的根本原因是什么？”那么，是組織學生按照教材規定的路徑來學習，還是遵循學生的認知活動線索重新設計課堂教學進程？這體現了教師不同的教學價值取向。

教學片段1：在觀察和比較等活動中，引發猜想。

1.出示：算一算，比一比，你有什么發現？

（1） 40÷10= ? ? （2） 60÷20=

8÷2= ? ? ? ? ? ? ? 120÷40=

（3） 9÷3= ? ? ? ? （4） 150÷30=

90÷30= ? ? ? ? ? 5÷1=

要求學生分組口算出結果之后，教師引導觀察與比較：

師：觀察這四組算式，你有什么發現？

生：每組算式中商都相等。

四組算式集中呈現“商相等”的共同特點。對學生而言，這是一種強刺激。它既是促使學生深入探究商不變的規律的思維“導火索”，又是引發學生繼續思考興趣的“引擎”。

師：我們知道任何事情發生都是有原因的。有沒有人想過：每組算式的商為什么都相等？

全班學生隨即沉默下來，陷入了思考之中。

顯然，由于學生年齡特征和認知水平的局限，從四組算式中，他們僅僅捕捉到“商相等”的表面現象。換句話說，學生的思維只是停留在知識的表層上，需要教師“站出來”發揮引導者的作用：“我們知道任何事情發生都是有原因的。有沒有人想過：每組算式的商為什么都相等？”將學生的思維引向“深水區”，從而透過“現象”探求隱藏其背后的本質。

師：比較每組中上下兩道算式的“被除數”“除數”有什么變化？

假如將這四組算式按照一定標準分類，你認為可以分成幾類？怎樣分？

學生獨立思考之后，先小組交流，再全班交流。

生：分成兩類：（1）（4）兩組為一類;（2）（3）兩組為一類。

師：為什么這樣分？

生：我發現（1）（4）兩組算式中被除數和除數同時變小了;而（2）（3）兩組算式中被除數和除數同時變大了。

師：繼續觀察思考，說說（1）（4）兩組算式中被除數和除數，因為什么同時變小？而（2）（3）兩組算式中被除數和除數，又因為什么同時變大呢？

生：（1）（4）兩組算式中被除數和除數同時除以一個數，所以變小;（2）（3）兩組算式中被除數和除數同時乘以一個數，所以變大。

師：能舉出實例說一說嗎？

（學生回答略）

師：通過這段時間的討論和交流，你又有什么新發現？

生：被除數和除數同時乘以同一個數，商不變;或被除數和除數同時除以同一個數，商不變。

師：為什么強調同一個數？舉例說一說。

（學生回答略）

對于學生而言，從感知到發現每組算式中“被除數和除數同時乘或除以一個數（0除外）”是商不變現象客觀存在的根本原因，屬于認知上的難點。為了有效突破教學難點，這里分兩個層次來教學：第一層次，在引導學生觀察比較每組算式中的被除數和除數的變化的基礎上，通過分類活動，促使學生初步感知每組算式的基本特征。當學生經過觀察、比較、分類和交流等活動時，初步發現“（1）（4）兩組算式中被除數和除數同時變小了;而（2）（3）兩組算式中被除數和除數同時變大了”，也就邁出了突破教學“瓶頸”的第一步。第二層次，在學生已有的感性認識的基礎上，繼續引導學生的思維向縱深延伸，從而建立被除數和除數共同變化的表象。“說說（1）（4）兩組算式中被除數和除數，因為什么同時變小？而（2）（3）兩組算式中被除數和除數，又因為什么同時變大呢？”這一問，又一次激蕩起學生思維的漣漪。他們沿著原有的思維路徑繼續探索前行，利用加、減、乘、除一一試算和思考，進而發現“被除數和除數同時乘或除以一個數（0除外）”與“商不變現象”之間的依存關系，并初步抽象和概括商不變的規律。

教學片段2：在具體實例計算中，驗證猜想。

1.引導驗證：

師：我們從四組除法算式中發現的除法中蘊含的“商不變的規律”是否可信？這里需要——

生：驗證！

出示：已知8400÷40=210，如果被除數和除數同時乘或除以一個數，商有什么變化？endprint

學生自主列舉試算（用計算器），之后小組交流，全班交流。

生：8400和40同時乘或除以相同的數，商不變。

師：請你具體說一說。

（學生回答略）

師：自己再找一些例子用計算器計算，而且這些例子要有代表性。比如不僅要包含一、兩位數，而且要包含三、四位數等等。看看是否都有這樣的規律？能否找出反例？然后，小組交流。

“我們從四組除法算式中發現的除法中蘊含的商不變的規律，是否可信？這里需要——”此時，繼續舉例計算驗證，就成為全體學生共同的心里需求。尤其是在初步驗證的基礎上，教師提出“選擇面要廣”“尋找反例”的要求，更能刺激學生的大腦神經，從而引發他們深入思考、踴躍地投入到計算驗證活動之中。

2.歸納概括：

師：通過舉例驗證，你能得出什么結論？

生：在除法中，被除數和除數同時乘或除以一個相同的數，商不變。

師：有沒有找到反例？

生：沒有！

師：想一想：為什么被除數和除數同時乘或除以相同的數，商不變呢？

生：因為被除數和除數同時發生相同的變化！

通過親身經歷商不變的規律的“猜想——驗證——結論”的探究過程，學生從中獲得的不僅有數學知識，更有豐富的感知及深切的體驗。在此基礎上，教師拋出“為什么被除數和除數同時乘或除以相同的數，商不變呢？”一問，從而引領學生適度“觸摸”和追尋商不變規律的深層內涵，已然成為可能。當然，受學生知識水平的限制（利用分數和除法之間關系等知識推演），這里的引申“點到為止”，主要是適當提升學生思維概括水平。

3.思辨結論：

師：打開課本讀一讀“商不變的規律”，和我們概括的有什么不同？

生：有0除外。

師：為什么要0除外呢？

生：0不能作除數。

生：0作除數沒有意義。

教學片段3：在實際應用中，鞏固延伸。（略）

一般來說，教材為學生的數學學習提供了具有邏輯性、系統性的知識體系。能否把作為思維結果的數學加工成“活動的”、學生自己重新建構的數學，實現知識“再創造”，這既反映出教學設計的指導思想，又反映了教師不同的教學價值觀。

一、 突出探索性，培養學生思維能力

比如教學“商不變的規律”。單從知識教學的目標來看，按照教材例題提供的學習線索，也許能夠多快好省地探索發現商不變的規律。但是，從發展學生思維能力的角度來看，它卻完全屏蔽了從感知到領悟“被除數和除數同時乘或除以一個數（0除外）”與“商不變”之間因果關系的思考過程。如此教學，不僅不利于數學知識的建構，更不能最大限度地發揮“商不變規律”教學的“育人”功能。為此，教師在教學設計時，需要適度拉長教材空間，增強教學的探索性。尤其在學生“首次”感知實例，作出商不變規律的猜測環節，讓他們的思維“多飛一會兒”，從而充分領受發現之旅的“沿途風景”。

二、 突顯過程性，培養學生思維能力

比如“圓的周長”教學。一般教材側重點都是引導學生經歷圓周率的“猜測——驗證——結論”的探究過程。這其中“猜測”環節是探究學習的關鍵一步。蘇教版數學教材五年級下冊提供的教學路徑是：首先，讓學生觀察比較三個不同規格的自行車輪滾動一圈的路線長短，在此基礎上，引出圓的周長含義;接著，提出“比較三個車輪的直徑和周長，你有什么發現？”由此可見，學生僅僅從直觀比較中，感性地認識到圓的周長與其直徑大小有關。然而，這對幫助學生認識圓的周長和直徑之間倍比關系，以及引發他們實驗探究活動來說，并沒有多少指向性意義。更重要的是，學生失去了一次鍛煉思維能力和創新活動的機會。為此，一位教師“匠心獨運”憑借圖形直觀，引導學生多次觀察思考，逐層感知和推測圓的周長及其直徑之間關系。既收獲了知識，又提升了能力，收到了較好的效果。

1.大膽猜測，圓的周長和直徑之間有什么關系？

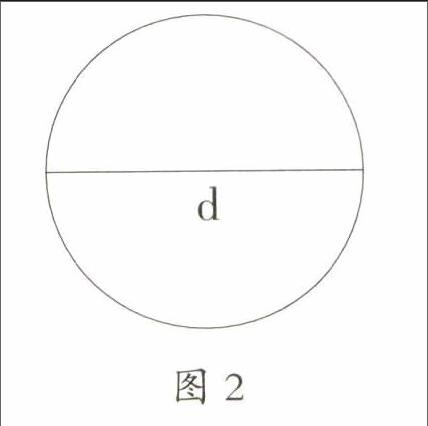
學生根據“兩點之間線段最短”的知識經驗，初步作出合理判斷：圓的周長>2直徑。

2.用心推測，圓的周長和直徑之間有什么關系？

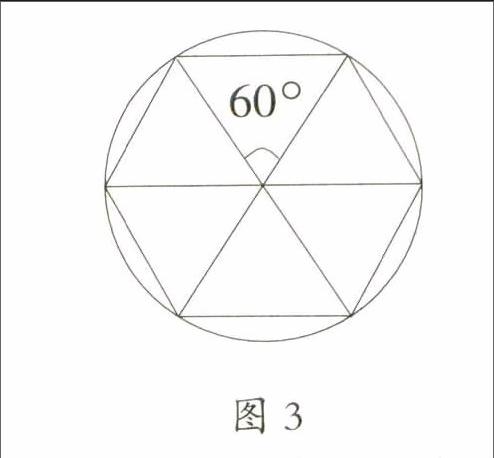
（1）

學生根據正六邊形的邊長=圓的半徑，以及直徑=2半徑等知識經驗，由正六邊形的周長<圓的周長，推導出：圓的周長>3直徑。

（2）

學生根據正方形的邊長=圓的直徑，由正方形的周長（4d）>圓的周長，推導出：圓的周長<4直徑。

（3）歸納：3直徑<圓的周長<4直徑。

案例中，每位學生基于已有的知識和經驗，積極參與觀察、比較、推理和歸納等活動，親身經歷“圓的周長和直徑之間關系”的猜想、推測等探究思考過程，不僅初步認識了圓的周長和直徑的倍比關系，為后續實驗探究指明了方向，更重要的是，傾聽了知識的“萌發”“生長”和“拔節”的聲音，提高了數學素養，發展了思維能力。

【責任編輯：陳國慶】endprint