對角占優矩陣的判定條件
田素霞
(商丘師范學院計算機與信息技術學院,河南 商丘476000)
對角占優矩陣及M-矩陣是計算數學和矩陣理論研究的重要課題之一。本文利用α-對角占優矩陣給出了廣義對角占優矩陣和分塊對角占優矩陣的判定條件,改進和推廣了文1-3的結果。

定義1 設A=(aij)∈Cn×n,若則稱A為嚴格對角占優矩陣;若存在正對角矩陣X使得AX為嚴格對角占優矩陣,則稱A為廣義嚴格對角占優矩陣.
定義2 設A=(aij)∈Cn×n,若存在α∈(0,1]使則稱A為嚴格α-對角占優矩陣;若存在正對角矩陣X使得AX為嚴格α-對角占優矩陣,則稱A為廣義嚴格α-對角占優矩陣.

設A=(aij)∈Cn×n,把A分塊為:

這里Aii(1≤i≤k)為ni階方陣
定義4 設A=(aij)∈Cn×n,分塊如(1),若Aii(1≤i≤k)均非奇異,且:

則稱A為塊對角占優矩陣;如果(2)的所有不等號為嚴格不等式,則稱A為塊嚴格對角占優矩陣;若存在正對角矩陣X使得AX為塊嚴格對角占優矩陣,則稱A為廣義塊對角占優矩陣.
設A=(aij)∈Cn×n,分塊如(1),且Aii(1≤i≤k)均非奇異,構造B如下:

引理1[1]設A=(aij)∈Cn×n,若A為嚴格α-對角占優矩陣,則A為廣義嚴格對角占優矩陣.
引理2[1]設A=(aij)∈Cn×n,分塊如(1),且Aii(1≤i≤k)均非奇異,構造B如(3),則A為廣義塊對角占優矩陣當且僅當B是非奇異M-矩陣.
定理1 設A=(aij)∈Cn×n,若N1∪N2=N,N1∩N2=?及α∈(0,1]存在使得滿足:

則A為廣義嚴格對角占優矩陣.
證明:令:

當i∈N1時,
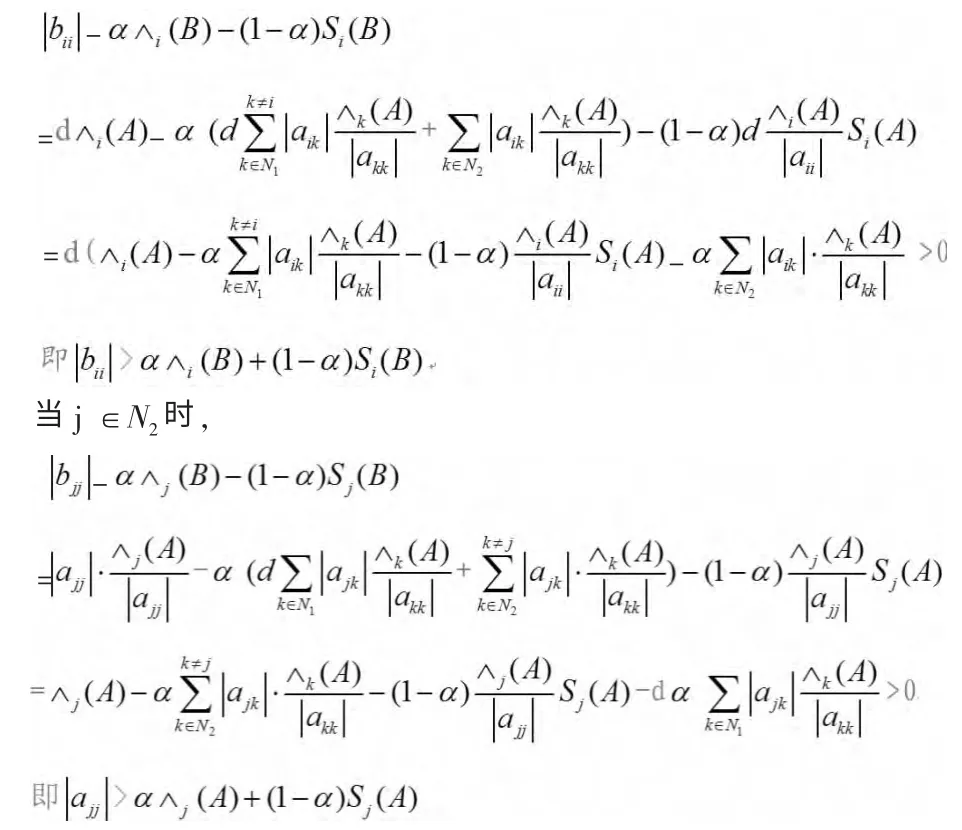
所以B為嚴格α-對角占優矩陣,由引理1知B為廣義嚴格對角占優矩陣,又因為X為正對角矩陣,所以A也是廣義嚴格對角占優矩陣。
定理2 設A=(aij)∈Cn×n,分塊如式(1),且Aii(1≤i≤k均非奇異,構造B如式(3),若若存在M1∪M2={1,2,…∈,k},M1∩M2=?及α∈(0,1]使得滿足:則A為塊廣義對角占優矩陣.
證明:由定理1知,如果滿足定理2的條件,則B是非奇異M-矩陣,由引理2知,A為塊廣義對角占優矩陣.

[1]孫玉祥.廣義對角占優矩陣的充分條件[J].高等學校計算數學學報,1997(3):216-223.
[2]高益明.矩陣廣義對角占優和非奇的判定(Ⅱ)[J].工程數學學報,1998(1):12-17.
[3]陳神燦.奇異M矩陣和廣義對角占優矩陣的實用判定準則[J].高等學校計算數學學報,2000(1):36-40.
[4]蔣正新,施國梁.矩陣理論及其應用[M].北京:北京航空學院出版社,1998.

