無傘無翼子彈藥氣動仿真及落點散布研究
李堯堯,姜春蘭,茶曉燕
(1 北京理工大學 機電學院,北京100081;2 中船重工第705研究所昆明分部,昆明650118)
常規(guī)的拋撒系統(tǒng)多采用傘-彈系統(tǒng)結(jié)構(gòu)布局[1],此布局有如下主要缺點:①傘-彈系統(tǒng)速度降快,留空時間長,易受到敵方機動目標的攻擊;②傘-彈系統(tǒng)極易受到隨機風的干擾;③阻力傘占用空間較大,影響裝填量。無傘無翼靈巧子彈藥系統(tǒng)是一種新型氣動結(jié)構(gòu)末敏彈,子彈系統(tǒng)留空時間短,下降速度快,能提供穩(wěn)態(tài)掃描和戰(zhàn)斗部激發(fā)平臺,占用空間小,增加了子彈裝填量。其針對面目標、集群目標的攻擊具有良好的費效比,在國外已經(jīng)被成功研制并參加了實戰(zhàn)[2]。該類靈巧子彈是強非對稱體,其運動規(guī)律具有強非線性、大攻角、存在奇異點等復雜特性。為使子彈藥具有良好的彈道一致性,較小的落點散布誤差,必須掌握無傘無翼靈巧子彈系統(tǒng)的氣動特性和標定4枚子彈藥拋撒彈道散布特性的影響因素。
1 子彈藥系統(tǒng)氣動仿真分析
1.1 彈體CFD建模及仿真
準定常假設下,采用靈活性好、外形適應能力強的非結(jié)構(gòu)化網(wǎng)格;網(wǎng)格劃分采用GANBIT軟件;求解器采用FLUENT6.3.26軟件。無傘無翼靈巧子彈藥彈道飛行均處于低馬赫數(shù)范圍,采用S-A模型,采用較大粘性參數(shù),物性參數(shù)和其他參數(shù)均采用軟件默認設置。總計算區(qū)域為圓柱體,長為8倍彈長,半徑為2倍彈長,根據(jù)彈體氣動流場分布,共劃分為5層約101萬個非結(jié)構(gòu)化網(wǎng)格。選擇Density-Based密度基求解器,Explicit顯式格式。動量方程對流采用二階迎風格式。S-A模型對有逆壓梯度邊界層問題能夠給出很好的計算結(jié)果,較好地應用于空氣動力學問題。靈巧子彈體外形如圖1所示。

圖1 子彈藥外形圖
1.2 彈體不對稱對氣動特性的影響
彈體表面壓強分布反映彈體在飛行過程中的空氣動力特性。當來流氣體與彈體相遇時,受到彈體的阻擋,則彈頭部壓強最大。經(jīng)過CFD仿真分析,彈體一側(cè)有部分凸出單元體時,氣流有不對稱現(xiàn)象,但對子彈藥整體氣動流場影響不大。
1.3 子彈藥系統(tǒng)氣動力分析
對靈巧子彈藥在速度v=25m/s,35m/s,40m/s,攻角α=0°,±2°,±4°,±6°,±8°,±10°時的氣動特性進行仿真。圖2~圖5分別為子彈藥阻力系數(shù)Cx、升力系數(shù)Cy、偏航系數(shù)Cz、俯仰阻尼力矩系數(shù)Mx隨攻角的變化曲線。CFD建模及仿真結(jié)果表明,阻力系數(shù)主要由氣動外形自身產(chǎn)生,隨攻角的變化不大;攻角對升力系數(shù)影響較大,對偏航系數(shù)影響較大。隨攻角增加,彈體壓心會逐漸靠近質(zhì)心,彈體逐漸趨向不穩(wěn)定,俯仰阻尼系數(shù)隨著攻角絕對值的增大也開始變化劇烈。
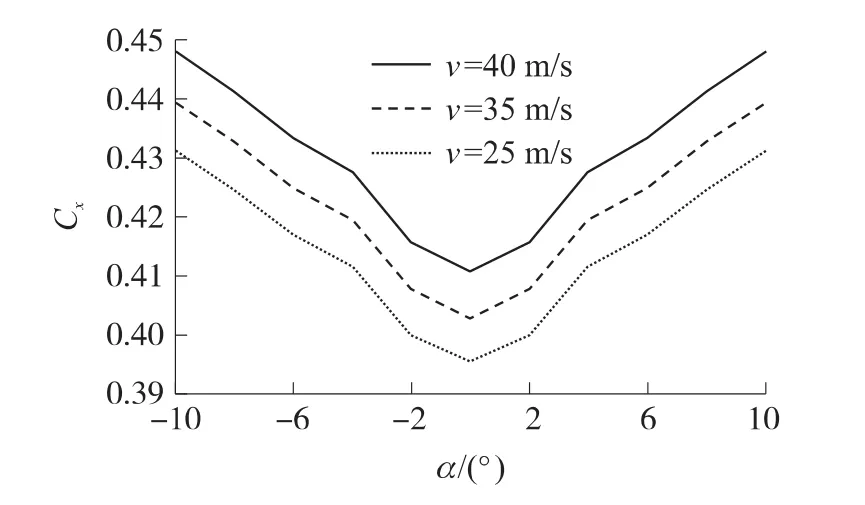
圖2 阻力系數(shù)-攻角的變化曲線
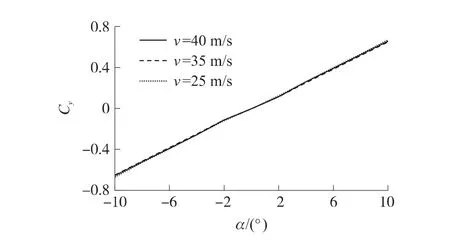
圖3 升力系數(shù)-攻角的變化曲線
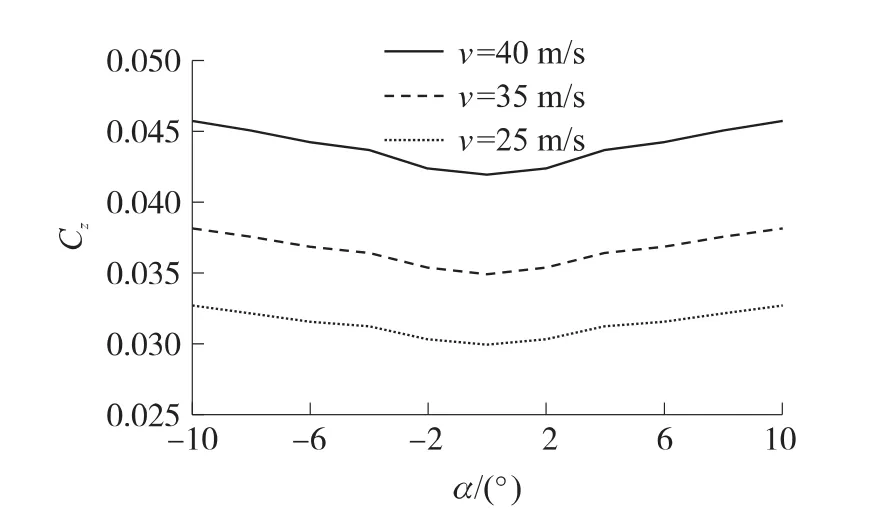
圖4 偏航系數(shù)-攻角的變化曲線
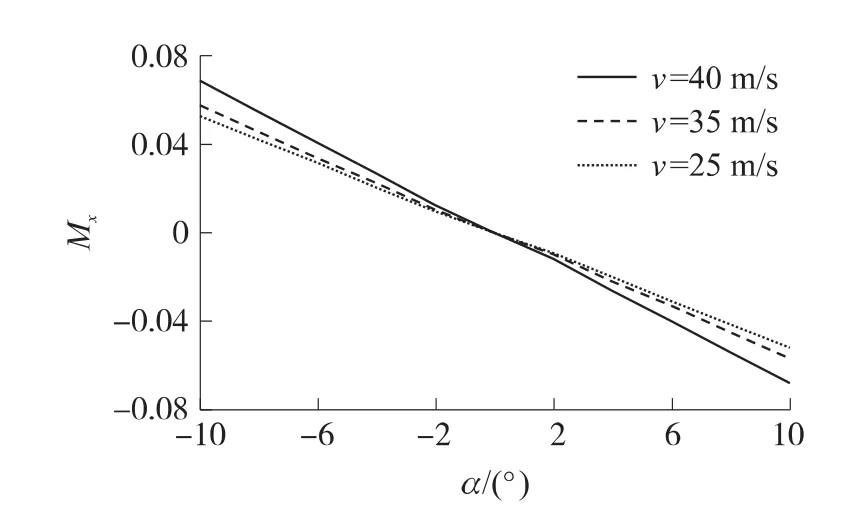
圖5 俯仰阻尼力矩系數(shù)-攻角的變化曲線
1.4 氣動外形特性分析
彈體不對稱對子彈藥整體氣動流場影響不大;攻角對阻力系數(shù)影響不大,攻角對升力系數(shù)影響較大。根據(jù)阻尼力矩系數(shù)曲線結(jié)合子彈藥擺動運動的運動方式,彈體整體氣動特性為靜不穩(wěn)定狀態(tài),需要在設計中采用一定旋轉(zhuǎn)速度和質(zhì)量偏心方能保持穩(wěn)定。
2 靈巧子彈落點散布分析
2.1 無傘無翼靈巧子彈藥彈道方程
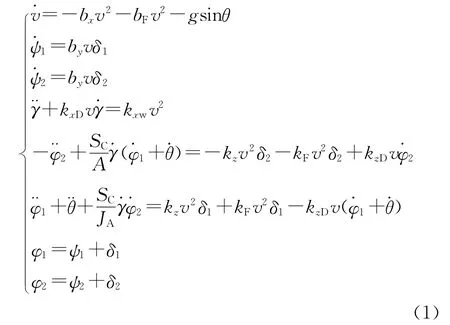
在速度坐標系下對受力進行投影,并結(jié)合坐標系角度轉(zhuǎn)換關系推導出拋撒過程彈道方程[3]:例關系,落點間距受拋撒高度影響很大[4]。拋撒速度vx分別為22m/s,26m/s,30m/s,34m/s和38 m/s時子彈藥的落點散布如圖7所示,子彈藥相對集束筒的拋速乘以落地時間就形成了落地間距,所以速度越大落地間距就越大。其對子彈群中心落點散布并不顯著,拋速由集束筒的小型旋轉(zhuǎn)發(fā)動機設計轉(zhuǎn)速決定。

圖6 拋撒高度對子彈落點散布的影響
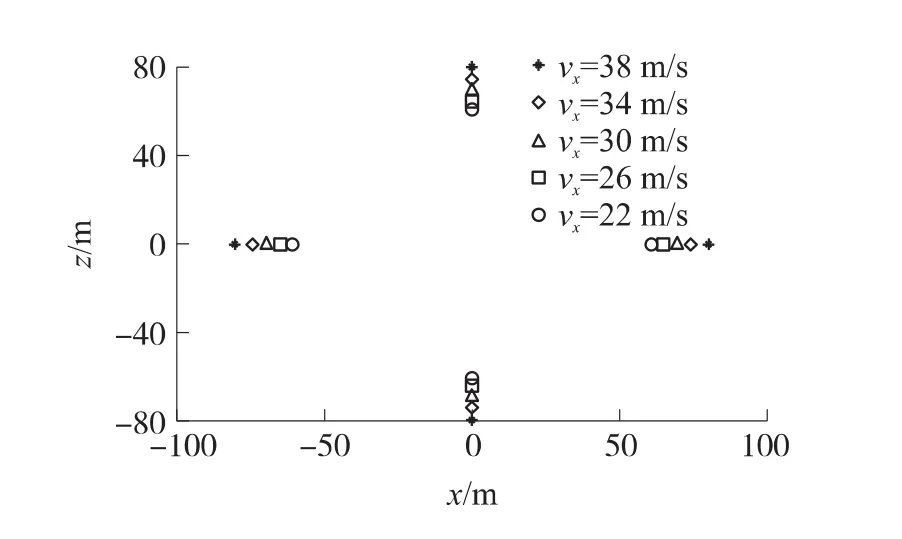
圖7 拋撒速度對子彈落點散布的影響
其中:
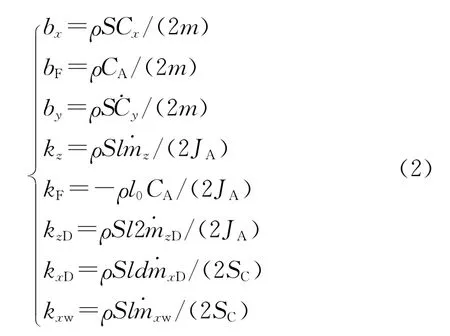
式中:δ1,δ2分別為俯仰角、偏航角,θ為彈道傾角;為赤道阻尼力矩系數(shù)導數(shù);SC為阻力面積,l為彈長為俯仰力矩系數(shù)導數(shù),S為彈體橫截面積,JA為赤道轉(zhuǎn)動慣量,ρ為空氣密度,Cx為切向阻力系數(shù),CA為側(cè)向阻力特征值為升力系數(shù)導數(shù),m為拋撒子彈藥質(zhì)量,d為彈徑為極阻尼力矩系數(shù)導數(shù)為尾部倒轉(zhuǎn)力矩系數(shù)導數(shù),其余為常規(guī)坐標系轉(zhuǎn)換角。
2.2 落點散布影響因素分析
拋撒高度hb分別為80m,100m,120m,140m和160m時子彈藥落點散布如圖6所示,拋撒高度直接決定子彈藥落地時間,時間和落地間距成正比
彈道傾角θ分別為50°,60°,70°,80°,90°時的子彈藥落點散布如圖8所示。彈道傾角影響著子彈群的中心落點,子彈藥落點間隔距離隨著彈道傾角增加而減小。在彈道傾角90°時,子彈群具有最好的落點散布情況。但是系統(tǒng)設計采用80°彈道傾角時較好實現(xiàn),且具有較好的系統(tǒng)設計實用性和穩(wěn)定性。子彈藥的豎直存速vy分別為20m/s,30m/s,40m/s,50m/s,60m/s時的子彈藥落點散布如圖9所示,從圖中可見,落點間距隨子彈藥豎直速度的增加而減小,其中
子彈藥阻力系數(shù)Cx分別為0.02,0.04,0.06,0.08,0.1時子彈藥落點散布如圖10所示。子彈藥落點間隔距離隨阻力特征的影響并不明顯,子彈藥落點散布較為均勻[5]。所以在考慮設計子彈藥外形時,尤其加裝側(cè)向探測裝置時,不用過多考慮阻力特征的影響。拋撒高度、子彈藥豎直速度、彈道傾角與子彈藥水平速度是設計子彈藥落點間距時需要認真考慮的重要因素。拋撒高度、子彈藥豎直速度則是子彈藥落點散布間距的重要考慮因素,而彈道傾角對子彈群的中心落點位置影響較大。
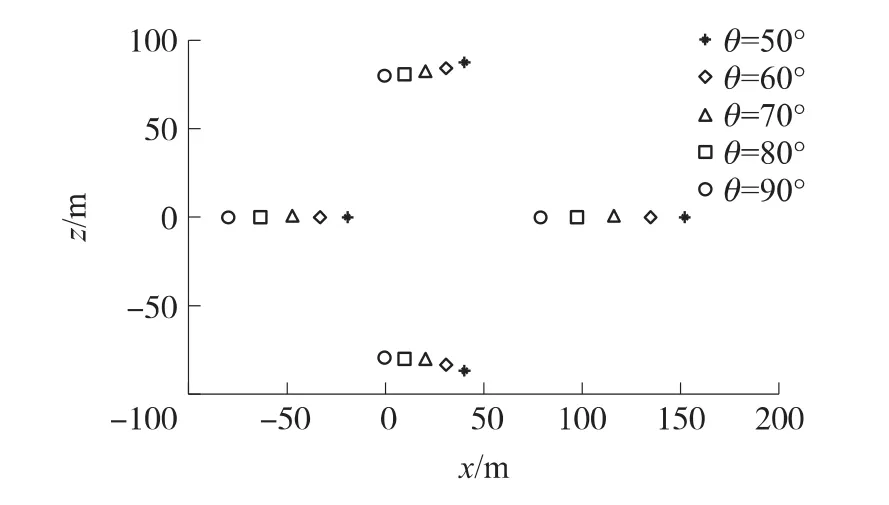
圖8 彈道傾角對子彈落點散布的影響
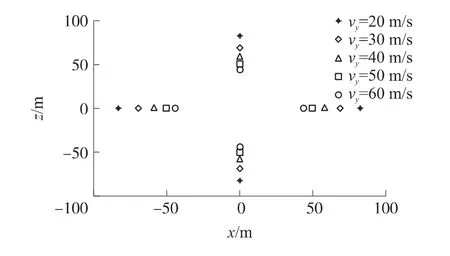
圖9 豎直速度對子彈落點散布的影響
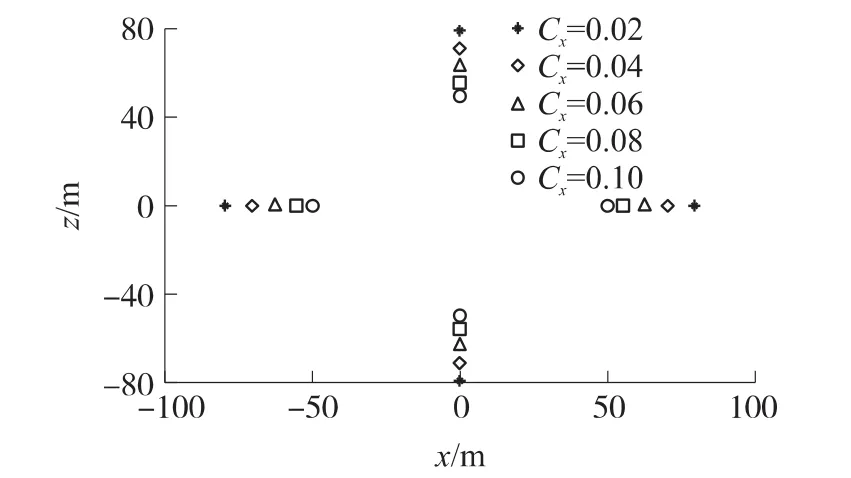
圖10 阻力特征對子彈落點散布的影響
3 結(jié)論
本文建立了無傘無翼靈巧子彈藥系統(tǒng)的動力學模型,應用CFD仿真進行了非對稱子彈藥氣動特性仿真分析,獲取了子彈藥系統(tǒng)阻力、升力、偏航、俯仰阻尼力矩數(shù)據(jù),為此種非對稱外形子彈藥的氣動設計提供了一定的技術支持。建立了飛行彈道方程組,編寫了彈道運算程序,仿真了系統(tǒng)拋撒過程中各因素對彈道落點散布的影響,分析并總結(jié)出了影響規(guī)律,本文的研究工作對相關無傘無翼靈巧子彈藥類系統(tǒng)分析設計提供了參考依據(jù)。
[1]楊紹卿.靈巧子彈藥工程[M].北京:國防工業(yè)出版社,2010.YANG Shao-qing.Smart munition engineering[M].Beijing:National Defense Industry Press,2010.(in Chinese)
[2]舒敬榮,姜勝平,李明軍,等.無傘雙翼末敏彈穩(wěn)態(tài)掃描段受力分析[J].彈道學報,2010,22(2):1-4.SHU Jing-rong,JIANG Sheng-ping,LI Ming-jun,et al.Force and moment analysis for double win terminal sensing ammunition without parachute at stable scanning stage[J].Journal of Ballistics,2010,22(2):1-4.(in Chinese)
[3]孫傳杰,盧永剛.一種無控子母彈落點散布分析[J].彈箭與制導學報,2010,30(1):109-111.SUN Chuan-jie,LU Yong-gang.Analysis of submunition distribution of an unguided cluster munition[J].Journal of Projectiles,Rockets,Missile and Guidance,2010,30(1):109-111.(in Chinese)
[4]曾必強,姜春蘭,王在成,等.傘彈系統(tǒng)落點散布影響因素分析[J].彈箭與制導學報,2010,30(1):105-108.ZENG Bi-qiang,JIANG Chun-lan,WANG Zai-cheng,et al.Research on the ballistic fall point spread of the parachute-bomb system[J].Journal of Projectiles,Rockets,Missile and Guidance,2010,30(1):105-108.(in Chinese)
[5]王中原,史金光,李鐵鵬.彈道修正中的控制算法[J].彈道學報,2011,23(2):19-21.WANG Zhong-yuan,SHI Jin-guang,LI Tie-peng.Control method for trajectory correction[J].Journal of Ballistics,2011,23(2):19-21.(in Chinese)

