導管架平臺的結構可靠性分析

張 婧，錢 鵬，王慶豐，江小龍

（江蘇科技大學船舶與海洋工程學院，江蘇 鎮江 212003）

0 引 言

海洋平臺是一種海洋工程結構物，它為開發和利用海洋資源提供了海上作業與生活的場所。隨著海洋開發事業的迅速發展，海洋平臺得到了廣泛的應用，如海底石油和天然氣的勘探與開發、海底管線鋪設、建造海上機場及海上工廠等。目前應用海洋平臺最為廣泛的領域當屬海上油氣資源的勘探與開發。

海洋平臺結構復雜，體積龐大，造價昂貴，與陸地結構相比，所處的環境非常惡劣，承受著多種隨時間和空間變換的隨機載荷（如波浪、海流、風、潮汐、海冰等載荷），同時還受到地震作用的威脅，在這種惡劣的工作條件下，海洋平臺的服役狀況不斷退化，其結構抵抗環境載荷作用的能力不斷下降。一旦發生事故，將造成重大的經濟損失和惡劣的社會影響[1]。

尋求結構的安全適用性和最佳的經濟效益，已經成為海洋平臺結構的設計、使用、檢測和維護中所必需關注的問題，而結構可靠度則是解決這一問題的最佳結合點。現階段人們雖然對結構可靠度的重要性已有所認識，但可靠度設計理論的發展遠不能滿足實際工程中對結構可靠性設計的要求[2～4]。所以，針對大型復雜結構，尋求有效而精確的結構可靠度計算方法十分重要。將有限元技術引入可靠性分析中，國內外學者采用Monte Carlo法及一次二階矩法開展了研究[4,5]。為討論基于有限元的隱式極限狀態方程的結構可靠性，Sudret等人開展了隨機有限元法的研究[6～8]；Teixeira、Soares等人開展了針對船舶平板、加筋板的響應面法研究[9]。本文基于ANSYS有限元軟件，結合MonteCarlo模擬提出復雜結構可靠性的計算方法，可以快速、準確的計算大型導管架平臺結構的可靠性指標，為結構設計提供更準確的依據。

1 導管架平臺失效模式的建立

1.1 應力失效模式

根據應力- 強度干涉理論，在海洋平臺的使用過程中，不允許出現應力超過屈服強度的事件發生，所以結構失效的準則為：

功能函數為

Gs(X)=σs-σmax(Xs)

式中：σmax——海洋平臺在服役過程中出現的最大應力；σs——材料的屈服強度；Xs——結構的材料、尺寸及外載荷向量。

1.2 位移失效模式

位移失效模式主要考慮結構產生的屈曲失效模式，選取結構分析中的最大位移點進行可靠性評估。載荷作用所產生的結構側移應小于規定的側移限值，因此結構的功能函數可表示為：

式中：Z——海洋平臺在服役過程中的側移限值；Zmax——海洋平臺在服役過程中出現的最大位移。

其中，對于復雜導管架平臺，結構響應σmax、Zmax的準確值需通過有限元分析得到，事實上，由式（1）、式（2）可知，復雜導管架平臺的可靠性時的功能函數均為隱式函數，其求解過程比較復雜，本文借助于Ansys軟件的APDL函數功能，進行相應的可靠性分析。

2 環境載荷

海洋工程結構物長期設置于海上從事生產作業，工作水域海況、氣象等環境條件對結構的安全，以及作業效率影響很大。因此，確定設計、分析中應該給予考慮的環境及氣象條件，是海洋工程結構物設計中的首要前提。海洋上的各類結構物大都處于開敞的海域，直接遭受波浪襲擊，受到波浪力的作用。海浪在靜水面附近波動最大，最活躍，靜水面附近的波浪力也就最大，減小這一區段結構尺寸，便可減小受力作用，導管架結構便是一個減小波浪力作用的較好結構形式。作用在海洋結構物上的波浪力與波高、波周期、水深、結構物尺寸及形狀等多因素有關。

在考慮波浪力時，采用Morison公式計算，認為波浪力是水流經物體時速度引起的阻力和水體加速度引起的慣性力的線性疊加，阻力是繞流時水質點運動速度突然變化而形成。波浪力的計算公式為：

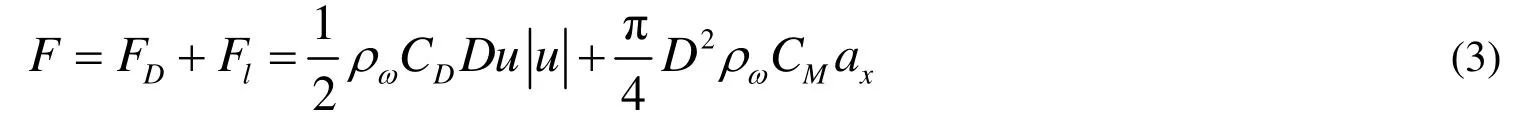
式中：F——垂直構件軸線方向上的單位長度的水動力矢量；FD——波浪阻力；Fl——波浪慣性力；CD——阻力系數，圓柱體構件取0.7；CM——慣性力系數，圓柱體構件取2.0；ρω——海水密度；D——構件的直徑；u——水質點的速度分矢量；ax——水分子的運動加速度。

風和流對于細長桿的作用力為：

式中：Cd——細長結構物的阻力系數，由經驗和試驗得到；ρ——流體密度；A——構件朝流體流速方向的投影面積；U——流速。

3 導管架平臺的可靠性分析

3.1 有限元模型的建立

導管架平臺屬于固定式平臺，由上層平臺結構和下部導管架組成，導管架底端通過樁基礎固定。上層平臺結構包括支撐框架和甲板。下部導管架由一系列鋼管焊接而成，主體是6根主導管，其間用細管作為撐桿，組成空間塔架結構，樁基礎通過主導管插入海底土層。有限元模型見圖1，其中平臺甲板上部設備的重量簡化為集中質量塊作用于甲板上，邊界條件為海底表面以下6倍樁徑處的剛性固定[10]。

整個模型采用三種單元類型：PIPE16、BEAM4、SHELL63。下部導管架和上部甲板框架的主要豎向支撐構件采用PIPE16單元，甲板平面的框架梁采用BEAM4單元，水平甲板采用SHELL63單元。PIPE16單元截面由外徑和厚度決定；BEAM4單元截面形式選用矩形，單元參數包括截面的高度、寬度、面積和截面慣性矩；SHELL63單元參數包括四節點的厚度。單元參數見表1。假設整個模型采用同一種鋼材，彈性模量EX=1.0× 1011Pa ，改為：EX=2.01E1011Pa 泊松比PRXY=0.3，密度DENS=7800 kg/m3。

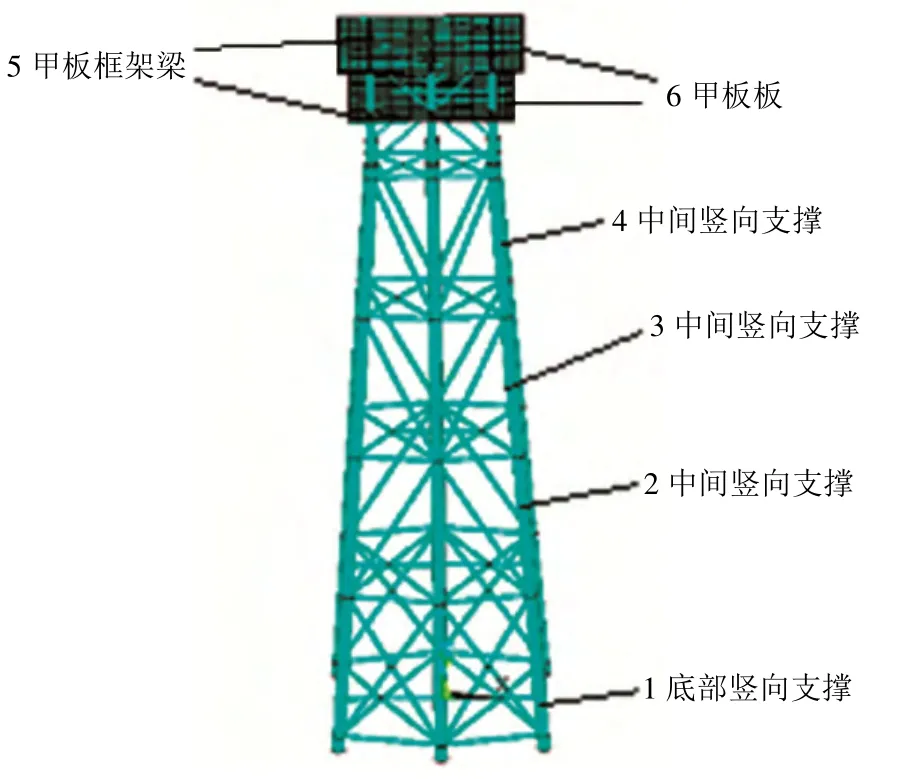
圖1 有限元模型

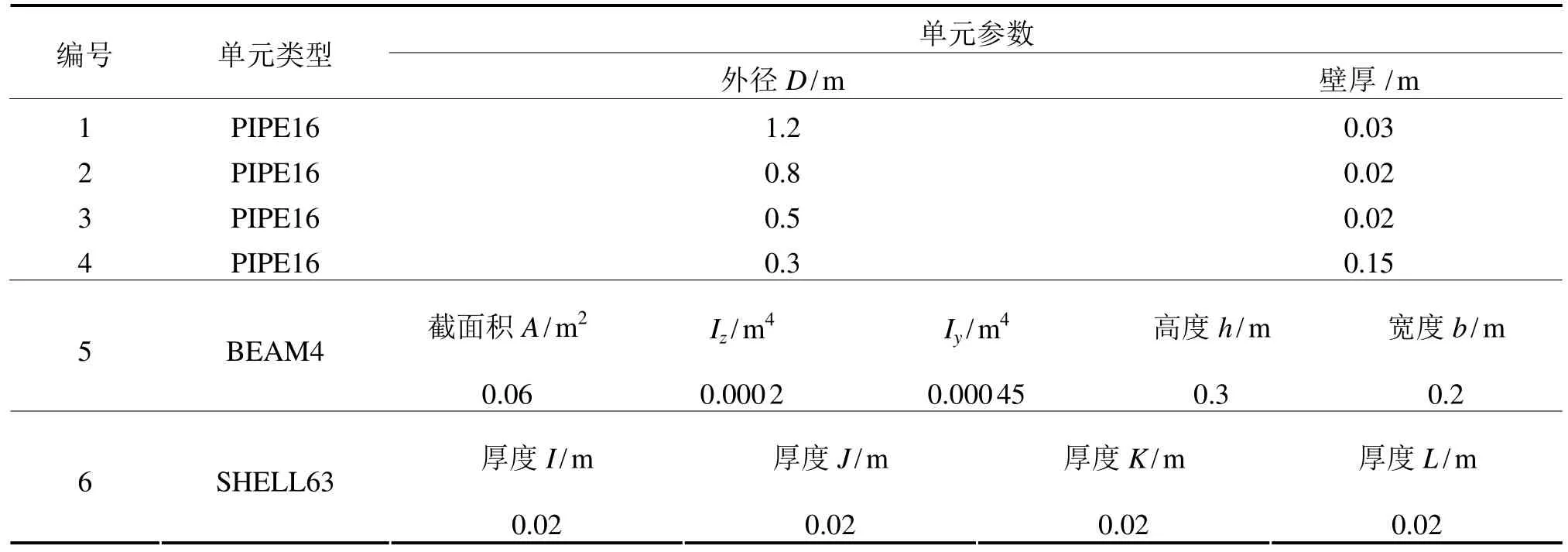
表1 單元參數

3.2 設計工況

該平臺位于墨西哥灣，選取典型設計工況見表2，其中工況5為該海域百年一遇的最大工況。

3.3 導管架平臺的靜力分析

對5種工況進行靜力分析，工況5的位移變形見圖2，應力圖見圖3。平臺的最大應力和最大位移見表3。

圖2 平臺位移

圖3 平臺應力

由圖2和圖3可知，最大位移處出現在平臺下方與導管架連接處，最大位移量為0.003601m，由導管架底座向上，越往上位移量越大。根據應力云圖最大應力處在導管架底與樁基的連接處，最大應力值為225MPa，略小于極限應力值。

表3 平臺的最大應力和最大位移

由表3知，前4種工況下的最大應力小于鋼材極限強度235MPa，結構是安全的。工況5最大應力處在導管架底與樁基的連接處，最大應力值為225MPa，略小于極限應力值。由于載荷的多變性與結構本身的不穩定性，結構可能發生破壞，需要進行可靠性分析。最大位移處出現在平臺下方與導管架連接處，最大位移量為0.003601m。

3.4 結構可靠性

3.4.1 設置變量

選取波浪載荷（工況5）、管徑、壁厚、極限應力值σ為變量，其中結構尺寸、材料參數的變異系數可參見文獻[11]。而本文對于波浪載荷進行了簡化的處理，基于 Morison公式和線性波理論開展其隨機性研究，其中僅考慮波高和波浪周期的變異性[12]，這是考慮了結構最不利的載荷情況。各變量初始值見表1，各輸入變量的參數分布見表4。

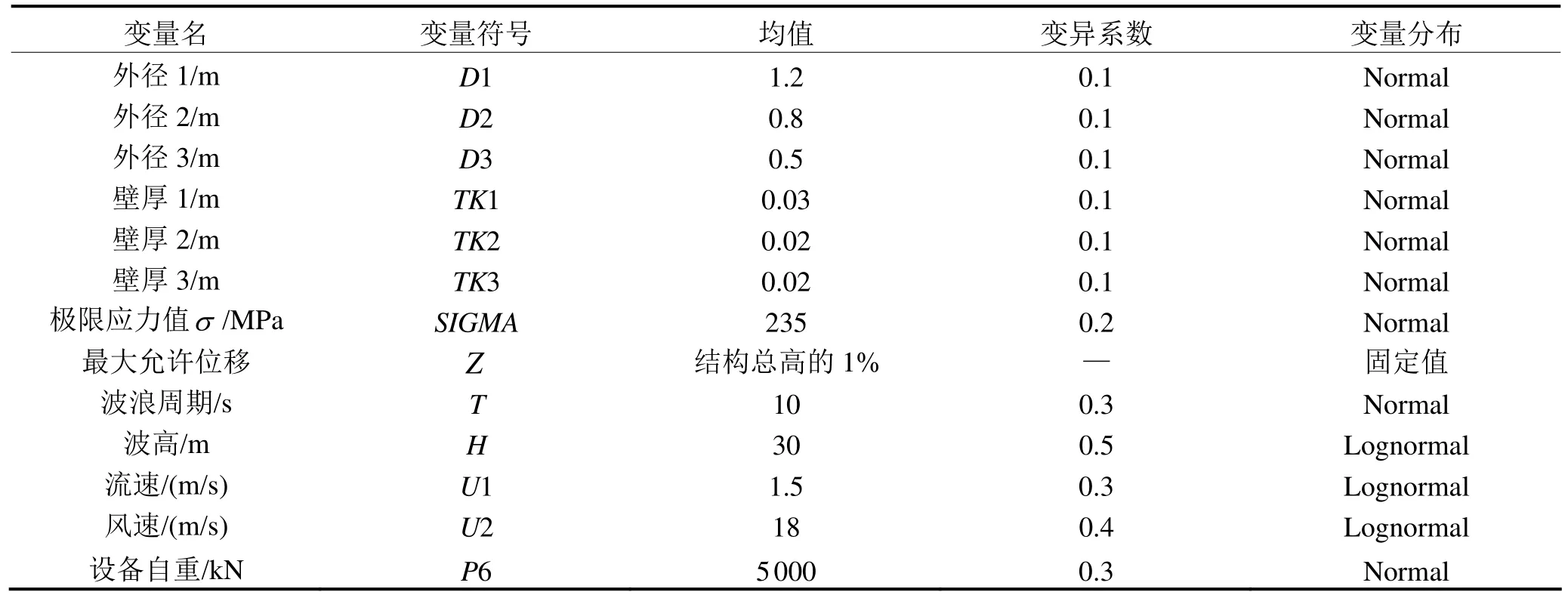
表4 輸入變量

3.4.2 定義失效函數并創建可靠性分析文件

后處理過程采用命令流方式建立可靠性分析文件，考慮極限工況下失效模式定義為應力失效（位移失效），命令流內容如下所示：

/POST1

NSORT, S, EQV

*GET, MAXSTR, SORT, , MAX

FF=SIGMA-MAXSTR/ FF=DIS-MAXDIS ！定義失效函數

LGWRITE, RELIAB_PLATEFORM, TXT ！創建可靠性分析文件

FINISH

3.4.3 可靠性分析

考慮了12個隨機變量，傳統的Monte Carlo方法需要進行大量的有限元分析才能獲得準確的計算結果，因此，采用重要抽樣法大大減少了計算時間[13]，其主要流程為利用Ansys的模塊調用外部程序（自編關于重要抽樣的Fortran程序），再通過Ansys本身的有限元模塊獲得結果。

圖4為隨機輸出變量FF的靈敏度。通過分析得出平臺應力失效可靠性指標β=4.91，位移失效β=3.56。由圖 4可知，影響最大應力取值的變量有：甲板上設備載荷P6、壁厚TK2以及管徑D2。其中重力P6影響最大，占≈1/2。其次是TK2和D2，這與實際情況是符合的，因為設備重力載荷是整個載荷結構中最大的載荷，且作用于甲板頂層，稍有變化，將會影響整個結構的最大應力值。

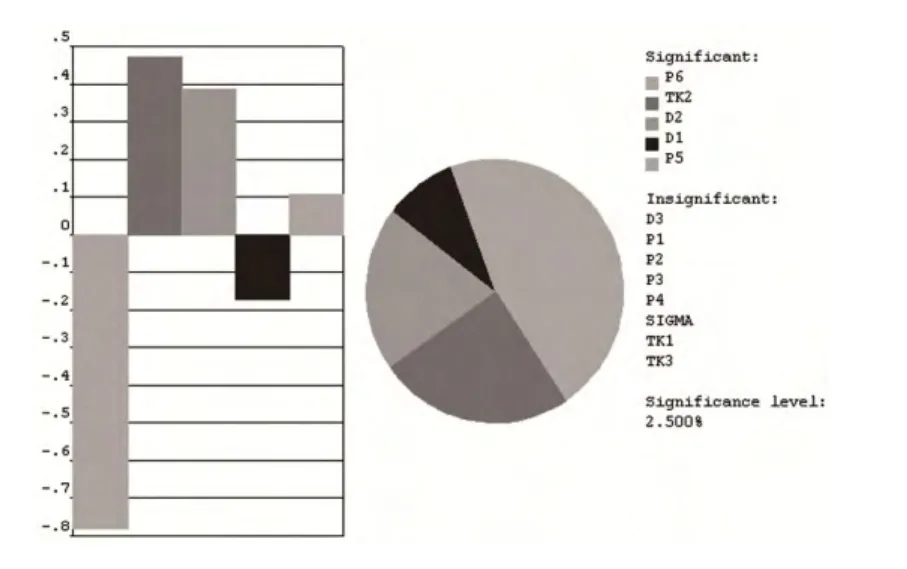
圖4 隨機輸出變量FF對隨機輸入變量靈敏度

4 結 語

1) 通過預設參數并選擇合適的分布函數和失效函數，對結構進行可靠性及靈敏度分析，可以確定對結構的應力和變形影響最大的參數，并在設計與制造的過程中加以預防；

2) 導管架平臺，由于其結構的特殊性，必須注意樁底和甲板與導管架連接處的設計，因為此處通常是應力與應變比較集中的部位；

3) 在利用ANSYS進行可靠性分析時，需要設定合適的變量，選擇合適的失效函數，根據變量參數的特點設定其合適的分布函數，這樣才能使分析結果更為準確，更加貼近實際，更具有實際參考意義。

[1] 宋 劍. 海洋平臺結構在偶然災害作用下的可靠性研究[D]. 浙江：浙江大學，2005.

[2] 趙國藩，金偉良，貢金鑫. 結構可靠度理論[M]. 北京：中國建筑工業出版社，2000.

[3] 安偉光. 結構系統可靠性和基于可靠性的優化設計[M]. 北京：國防工業出版社，1997.

[4] Melchers, R. E., Structural Reliability and Analysis Prediction, 2nd Edition, John Wiley & Sons. 1999.

[5] Shahid M., Das P. K.. Structural Reliability and Finite Element Methods[J]. International Shipbuilding Progress, 2008, 55(4):281-300.

[6] Sudret B., Der Kiureghian, A.. Comparison of Finite Element Reliability Methods[J]. Prob. Eng. Mech., 2002, 17 (4):337-348.

[7] Ghanem R. G., Spanos P. D.. Spectral Stochastic Finite Element Formulation for Reliability Analysis[J]. Journal of Engineering Mechanics, ASCE, 1991, 117 (10).

[8] 朱永梅，李成濤. 基于隨機有限元的空間梁板結構系統可靠性分析[J]. 江蘇科技大學學報：自然科學版，2010，24（6）：564-567.

[9] Teixeira A. P., Guedes Soares C.. Response Surface Reliability Analysis of Steel Plates with Random Fields of Corrosion,Safety, Reliability and Risk of Structures[J]. Infrastructures and Engineering Systems, Furuta, Frangopol & Shinozuka (eds),Taylor & Francis Group, London, Osaka, 2010:474-481.

[10] API. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design.2000, API Publishing services, N.W., Washington.

[11] Gaspar B., Naess A., Leira B. J., et al. Efficient System Reliability Analysis by Finite Element Structural Models[C].Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2011)Rotterdam, The Netherlands, Paper OMAE2011-49950.

[12] 楊鵬，顧學康，吳東偉.半潛平臺載荷不確定性及結構可靠性研究. 船舶力學[J]. 2012,16（1/2）：108-117.

[13] 袁修開，呂震宙，宋述芳. 失效概率計算的截斷重要抽樣法[J]. 西北工業大學學報，2007,25(5):752-756.