脫層缺陷夾層板的自由振動與運動響應(yīng)研究

楊心怡，葉仁傳，沈超明

（江蘇科技大學(xué) 船舶與海洋工程學(xué)院，江蘇 鎮(zhèn)江 212003）

0 引 言

自20世紀(jì)40年代的玻璃纖維增強塑料面世以來，復(fù)合材料產(chǎn)業(yè)發(fā)展迅猛。近年來，多種新型復(fù)合材料以其優(yōu)良的力學(xué)性能，在船舶和海洋工程領(lǐng)域得到了廣泛的應(yīng)用[1]。其中，在兩片金屬面板中間填充彈性體芯材而形成的三明治結(jié)構(gòu)的夾層板[2,3]，具有結(jié)構(gòu)簡單、自重輕、強度比和剛度比大、抗疲勞、防火及減振效果好等諸多優(yōu)點。由于現(xiàn)有的常規(guī)船用鋼材耐磨性能較差[4]，而其對溫度場的變化較敏感也會影響到整體船舶建造的精度[5]；其次，采用傳統(tǒng)鋼材建造的船舶結(jié)構(gòu)通常只能以加固受載部位的方式來處理沖擊載荷或爆炸載荷問題，而這將極大地增加船舶質(zhì)量，同時帶來諸多其他負(fù)面影響[6～8]；故國外已有很多機構(gòu)及公司開展了夾層板在船舶與海洋工程領(lǐng)域的應(yīng)用研究與實踐。其中，英國IE公司開發(fā)的鋼/聚氨酯夾層板已經(jīng)應(yīng)用在船舶與海洋工程結(jié)構(gòu)的建造和維修中，并以其優(yōu)越的性能受到美國海軍的高度重視，也獲得了英國、德國和挪威船級社的認(rèn)可。作為 21世紀(jì)重要的工程材料，夾層板的應(yīng)用越來越廣泛，尤其是在艦船上的應(yīng)用呈明顯上升趨勢[9]。然而，此類夾層板的面板和芯材連接通常采用黏結(jié)方式，因此在制造和應(yīng)用的過程中容易出現(xiàn)脫層和開裂等結(jié)構(gòu)損傷[10]。若不能及時對脫層情況進行評估，極易造成安全隱患。

關(guān)于完整夾層板的動態(tài)響應(yīng)行為已被廣泛研究，而關(guān)于脫層夾層板結(jié)構(gòu)的動態(tài)力學(xué)響應(yīng)問題雖然起步較早但進展緩慢，目前關(guān)于夾層板脫層的研究資料較為匱乏。早在1976年，Kachanov[11]就注意到由于脫層引起的復(fù)合材料結(jié)構(gòu)的破壞問題，Simitses等[12,13]考慮非線性變形，重新計算了脫層梁最大承載能力，詳細(xì)研究了脫層位置、尺寸和厚度對極限載荷的影響。Hong和Chen[14]在分層區(qū)上下子板間構(gòu)造一種特定的界面連接單元，以防止分層處子板間的嵌入現(xiàn)象，且利用時域直接積分法，對穩(wěn)態(tài)激勵下層合板的響應(yīng)特征進行的研究，為含層間分層損傷層合板的動力分析提供了一個有效方法，以上均通過理論方法對脫層行為進行研究，雖然能夠?qū)γ搶訆A層板的動態(tài)力學(xué)性能進行基礎(chǔ)的分析，但均不夠系統(tǒng)。隨著有限元技術(shù)的發(fā)展，對許多以前無法研究的問題提供了一種切實可行的方法，2012年V.N.Bur layenko等[15]首次應(yīng)用有限元軟件ABQUAS研究了一種存在脫層區(qū)域的四邊簡支板在諧振激勵荷載下的部分動態(tài)響應(yīng)問題。

在分析動力學(xué)微分方程和數(shù)值求解方法的基礎(chǔ)上，通過有限元軟件ANSYS/LS-DYNA分析了脫層對整體夾層板的自由振動以及在諧振荷載激勵下脫層區(qū)域?qū)A層板運動響應(yīng)的影響，并基于脫層夾層板相對于完好夾層板的運動響應(yīng)差異，給出了一種識別夾層板是否存在脫層情況的新方法。

1 有限元理論公式

對中心存在圓形脫層情況的矩形板在隨時間變化的載荷下的運動響應(yīng)作研究。脫層區(qū)域位于上下表面黏結(jié)處，其半徑為R。脫層板在外力作用下的動態(tài)響應(yīng)是非線性的，即使是在小位移和最簡單的線性本構(gòu)關(guān)系的情況下亦是如此。

1.1 彈性小變形動力學(xué)基本方程

線彈性小變形動力學(xué)動力基本控制方程[16]組如下：

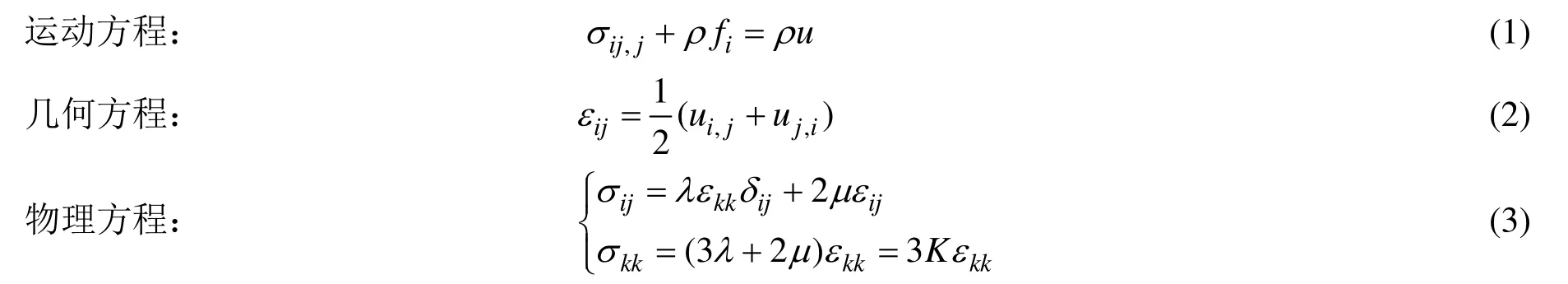
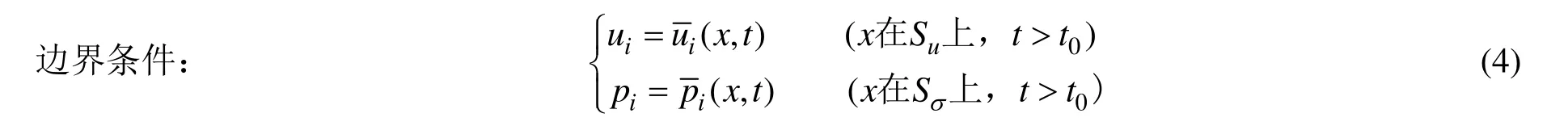
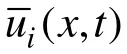
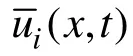
由于上述微分方程無法求解出一般性的解析解，因此只能通過數(shù)值方法求解所需的未知量。

1.2 彈性動力學(xué)數(shù)值計算方法

彈性動力學(xué)的數(shù)值計算方法是基于Hamilton變分原理，Hamilton變分原理的表述為：在一切可能的運動狀態(tài)中，真實狀態(tài)滿足式（5）的駐值條件：

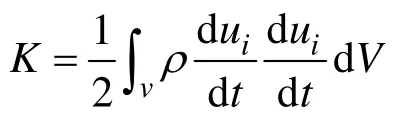
將K與U代入（5）式，并應(yīng)用散度定理可得：

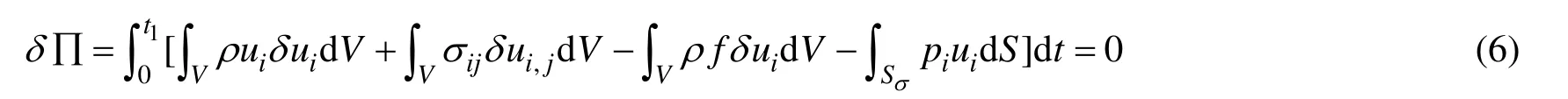
應(yīng)用有限元法直接計算泛函數(shù)駐值是將結(jié)構(gòu)空間離散化，在離散化的單元以及節(jié)點上進行位移插值，即

式中：NI——節(jié)點I的形函數(shù)。

將幾何方程與物理方程寫成矩陣形式為：

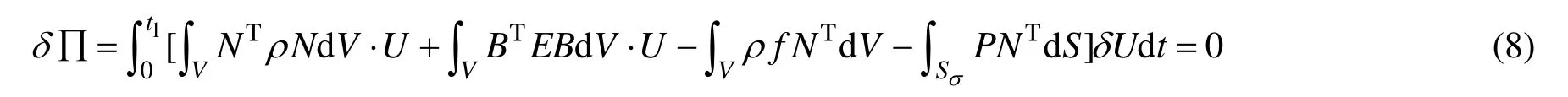
式（9）即為經(jīng)過有限元離散化后獲得的關(guān)于結(jié)構(gòu)動力響應(yīng)的二階常微分方程，將阻尼項引入動力學(xué)微分方程可得：

2 脫層夾層板的數(shù)值仿真

2.1 矩形夾層板參數(shù)與有限元模型

夾層板脫層區(qū)域位于矩形夾層板的中心，假設(shè)脫層區(qū)域形狀為圓形。矩形夾層板的平面尺寸為1m×1m，上下面板采用相同材質(zhì)，詳細(xì)的物理、幾何參數(shù)見表1。

表1 夾層板的物理參數(shù)、幾何參數(shù)

幾何模型與有限元模型見圖1，夾層板模型的上下面板和芯材均采用SOLID164單元，全部實體采用掃略網(wǎng)格劃分法，脫層區(qū)域位于面板的中心且假設(shè)脫層發(fā)生在上面板與芯材黏結(jié)面，其他區(qū)域完好；由于一般夾層板的脫層面積是變化的，為研究方便，取脫層半徑為R=0.1m，即脫層面積占面板總面積的3.14%，對于其他脫層面積可用相同的分析方法，面板與芯材之間的脫層區(qū)域運用面面自動接觸，其余未脫層的區(qū)域的面板與芯材共節(jié)點。夾層板四周約束條件為：四邊簡支約束，其數(shù)學(xué)表達式為：

載荷為諧振載荷位于上面板上表面中心節(jié)點處，大小為F(t)=Fsin(ωt)，結(jié)構(gòu)在受動載荷時的動態(tài)響應(yīng)不僅與結(jié)構(gòu)的本身固有特性有關(guān)，還與外載荷的激勵頻率密切有關(guān)，因此分析選擇5個不同的激勵頻率，其值依次為：250Hz，500Hz，1000Hz，1500Hz，2000Hz且幅值均為10kN。重點分析見圖1的P1、P2、P3、P4節(jié)點。

2.2 模態(tài)分析

有限元模態(tài)分析是建立模態(tài)分析模型并進行數(shù)值分析的過程，模態(tài)分析的實質(zhì)就是求解有限個自由度的無阻尼彈性系統(tǒng)方程。

運用體單元建立的有限元的模型見圖1，脫層區(qū)域運用無摩擦接觸，其余接觸部分采用固結(jié)形式。運用Block-Lanzos方法對完好的夾層板和脫層情況的夾層板有限元模型進行解析模態(tài)計算得到前20階的自振頻率（見表2）。

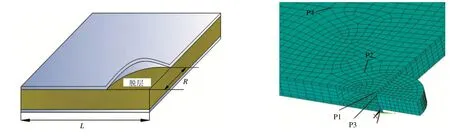
圖1 夾層板有限元模型及脫層區(qū)域特征分析位置

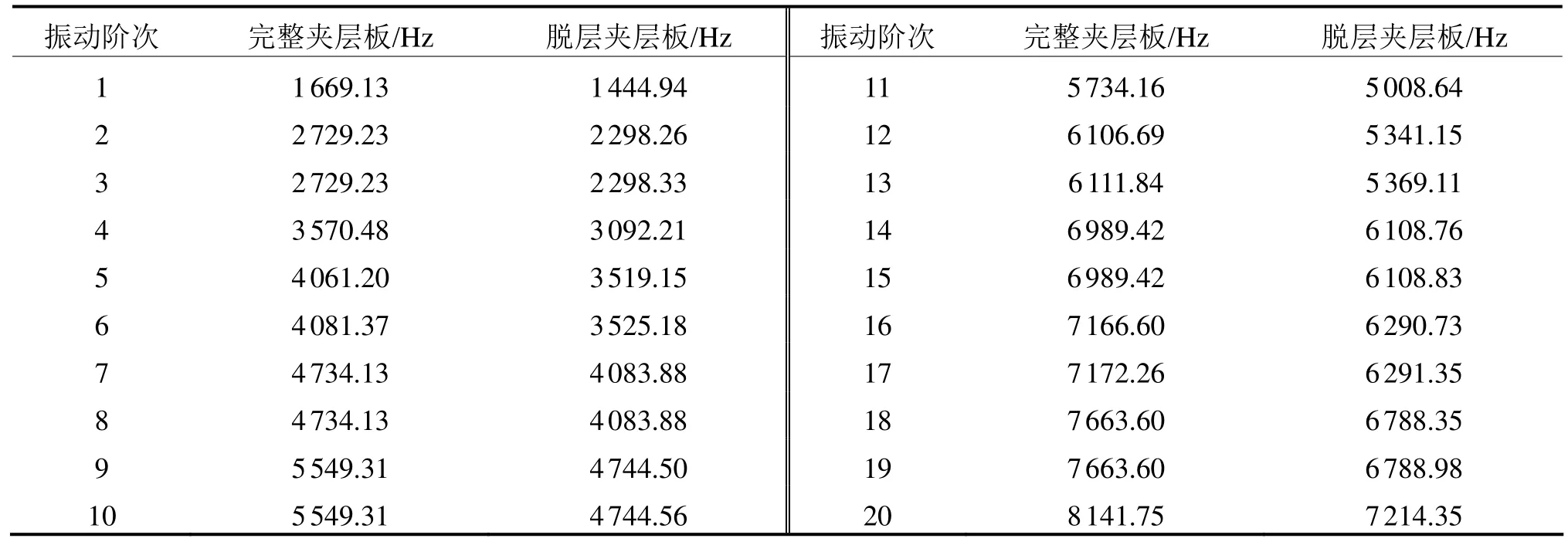
表2 完整夾層板和脫層夾層板的自由振動頻率

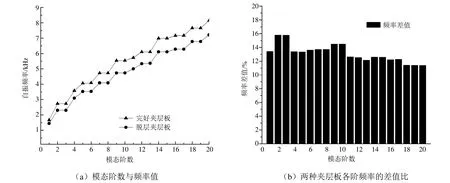
圖2 完整夾層板和脫層夾層板的自振頻率對比

從圖2（a）、（b）可知，在脫層面積占面板總面積的3.14%時，相同階數(shù)下完整夾層板的自振頻率均高于脫層夾層板，而且差值的變化范圍均在11%～16%之間，因此可以根據(jù)完整夾層板的自由振動頻率推測出夾層板在中心區(qū)域脫層面積為3.14%時各階自由振動頻率的大致范圍。

2.3 諧振載荷下夾層的運動特性

一般進行動力學(xué)分析前需對結(jié)構(gòu)進行模態(tài)分析，以確定結(jié)構(gòu)的自振頻率，從而避免結(jié)構(gòu)的設(shè)計載荷頻率與自振頻率相同或相近而發(fā)生共振。

針對完整和脫層兩種夾層板上4個代表性節(jié)點（見圖1）進行不同頻率下諧振載荷的動態(tài)響應(yīng)分析得知，兩者的P1點在不同頻率下的橫向位移歷程曲線見圖3，由圖中波形周期推算出的結(jié)構(gòu)響應(yīng)頻率與所施加的激勵頻率（分別為250Hz、500Hz、1000Hz、1500Hz、2000Hz）基本一致。對比圖3（a）、（b）可知，在相同的激勵頻率下，脫層夾層板在P1點的橫向位移明顯大于完整夾層板，而當(dāng)激勵頻率為500Hz時尤其明顯。對比表2分析可知，完整夾層板的一階振動頻率非常接近于1500Hz，由此可以確定位移突然增大是由于夾層板在一定程度上發(fā)生了共振；而脫層夾層板在500Hz頻率時也發(fā)生了共振，雖然脫層夾層板的基頻遠(yuǎn)大于500Hz，但仍然會發(fā)生共振，主要是由于脫層部分可以自由運動從而容易發(fā)生局部共振，因此針對脫層夾層板不僅要考慮整體的基頻還要考慮局部自振基頻值，就如同板架結(jié)構(gòu)的加強筋會發(fā)生局部共振一樣；從兩條發(fā)生共振的曲線上可以明顯看出其均存在一個包絡(luò)線，此現(xiàn)象的發(fā)生是由于激勵頻率與結(jié)構(gòu)的自振頻率雖然接近但并非完全一樣，中間存在一個差值，從而導(dǎo)致共振產(chǎn)生的橫向位移亦呈現(xiàn)周期性變化。另外，對不發(fā)生共振的情況進行分析發(fā)現(xiàn)在載荷幅值相同的情況下，頻率越大其對應(yīng)的最大位移越小，其主要原因是振動頻率越大其質(zhì)量慣性就越大，從而導(dǎo)致位移幅值反而減小。

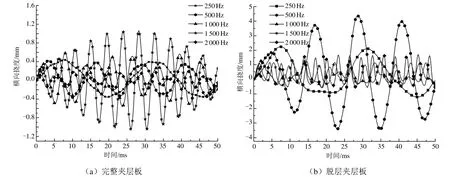
圖3 P1點在不同頻率下的橫向位移歷程曲線

由于實際設(shè)計結(jié)構(gòu)時均設(shè)法使其避免發(fā)生共振，因此選取一種未發(fā)生共振情況（250Hz，1000Hz）下完整夾層板和脫層夾層板在受載荷點（P1）的橫向位移見圖4，頻率為250Hz時完整夾層板和脫層夾層板的第一個極值橫向位移分別為0.362mm和1.273mm，后者是前者的3.52倍，頻率為1000Hz時完整夾層板和脫層夾層板的第一個極值橫向位移分別為0.45mm和2.25mm，后者是前者的5倍，因此脫層區(qū)域受載對整個夾層板結(jié)構(gòu)的危害極大。

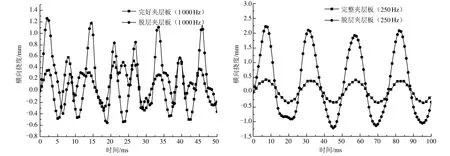
圖4 P1點相同頻率下完整夾層板和脫層夾層板橫向位移歷程曲線

2.4 夾層板脫層識別方法

在分析完整夾層板和脫層夾層板的動態(tài)特性問題的過程中發(fā)現(xiàn)完整夾層板的橫向位移-速度歷程曲線非常有規(guī)律而脫層夾層板的橫向位移曲線非常凌亂。因此，基于此結(jié)論提出了一種全新的識別夾層板是否脫層的方法。完整夾層板和脫層夾層板的4個點在1000Hz時的橫向速度-位移對比曲線見圖5，首先從4個點的橫向位移-速度曲線可以清晰地看出完整夾層板的曲線非常有規(guī)律，均接近于橢圓且關(guān)于零點基本對稱；而脫層夾層板在4個點的位移-速度曲線非常凌亂且最大正值明顯高于最大負(fù)值。

由于黏結(jié)而成的夾層板較容易發(fā)生脫層且不易被偵測，根據(jù)夾層板的橫向位移-速度曲線可以間接識別出夾層板是否存在脫層情況。例如，對于一塊完整的夾層板要想知道其內(nèi)部是否存在脫層的情況則可以在夾層板的中間某一區(qū)域施加諧振載荷或瞬時沖擊載荷，然后根據(jù)測量某些特征點的橫向位移-速度曲線來判斷夾層板是否存在脫層的情況。此種方法檢測夾層板脫層的方法機理簡單、操作容易且所需的儀器和設(shè)備較少，可以用任何簡便的方法來激振并測量夾層板某些特征點的位移歷程曲線，然后根據(jù)特征點的位移歷程曲線即可判斷夾層板是否發(fā)生脫層。

圖5 相同頻率下不同節(jié)點的橫向位移-速度曲線

3 結(jié) 語

針對完好夾層板和脫層夾層板的情況，對比分析了完好夾層板和脫層夾層板的自由振動和運動響應(yīng)變化并得出如下結(jié)論：

1) 在幾何尺寸與材料參數(shù)相同的條件下，完整夾層板在20階次以下的自由振動頻率均高于存在脫層缺陷的夾層板。當(dāng)脫層面積占夾層板面積的3.14%時，含有脫層缺陷的夾層板自由振動頻率降低11%～16%；

2) 諧振載荷作用下（不發(fā)生共振的情況），夾層板的最大位移隨諧振激勵頻率的增大而減小。在相同激勵頻率下，脫層夾層板的橫向位移明顯大于完整夾層板，其部分節(jié)點的最大橫向位移可達完整夾層板的5倍；

3) 諧振載荷作用下，完整夾層板節(jié)點的橫向位移-速度曲線均接近于橢圓且關(guān)于零點基本對稱，呈現(xiàn)出良好的規(guī)律性，而脫層夾層板節(jié)點的位移-速度曲線則非常凌亂，不具有規(guī)律性；由此可根據(jù)夾層板的橫向位移-速度曲線間接識別夾層板是否存在脫層缺陷。

[1] 白光輝. 復(fù)合材料船艇結(jié)構(gòu)選型及抗爆性能分析[D]. 哈爾濱：哈爾濱工業(yè)大學(xué)，2010.

[2] Kennedy S. J., Kennedy D. J .L. A True innovation: Steel plates with a structural elastomer core[A]. Proceedings of the 5th International Conference on Composite Construction in Steel and Concrete V, ASCE, 2006:114-126.

[3] 周艷秋，洪 明. 艦船用夾層板的力學(xué)特征與應(yīng)用[J]. 中國造船，2004, 45 (Sup 1): 79-85.

[4] 林海波. 疏浚系統(tǒng)耐磨材料的應(yīng)用研究[J]. 船舶與海洋工程，2012 (4): 60-62.

[5] 楊 振，劉建峰. 溫度場變化對船塢搭載精度控制的影響研究[J]. 船舶與海洋工程，2013 (3): 16-20.

[6] 顧君君，任廣智，劉志良. 多橋段裝船加固結(jié)構(gòu)設(shè)計計算[J]. 船舶與海洋工程，2013 (3): 65-69.

[7] 汪永茂，金 軍. 船舶導(dǎo)流管制造與焊接工藝研究[J]. 船舶與海洋工程，2012 (3): 69-73.

[8] 王 帆. 船用大型鑄鋼件焊接裂縫及修復(fù)工藝研究[J]. 船舶與海洋工程，2012 (4): 63-66.

[9] Rabczuk T, Kim J Y, Samaniego E, et al. Homogenization of sandwich structure[J]. International Journal for Numerical Methods in Engineering, 2004,(61):1009-1027.

[10] Luo G, Lv X. Dynamics of a plastic-impact system with oscillatory and progressive motions [J]. International Journal of Non-Linear Mechanics, 2008, 43(2): 100-110.

[11] Kachanov L M. Separation failure of composite materials [J]. Mechanics of Composite materials 1976, 12(5):812-815.

[12] Simitses G J, Sallam S, Yin W L. Effect of delamination of axially loaded homogeneous laminated plates[J]. AIAA Journal,1985, 23(9): 1437-1444.

[13] Yin W L, Sallam S N, Simtses G J. Ultimate axial load capacity of a delaminated beam-plate[J]. AIAA Journal, 1986, 24(1):123-128.

[14] Hong M, Chen H R. Dynamic behavior of laminated composite plates with delamination[J]. Ship Mechanics, 2000, 4(6): 28-38.

[15] Burlayenko V N, Sadowski T. Finite element nonlinear dynamic analysis of sandwich plates with partially detached facesheet and core [J]. Finite Elements in Analysis and Design, 2012, 62: 49-64.

[16] 金 澤. LS-DYNA3D 理論基礎(chǔ)與實例分析[M]. 北京：科學(xué)出版社，2005.