淺談函數極限計算的常用求法
2015-01-02 05:17:00張旭紅
科技視界 2015年4期
張旭紅
(北京信息職業技術學院基礎部,中國 北京100000)
極限概念是高等數學中最重要、最基本的概念,極限理論是數學分析的基礎理論,也是高等數學的重要思想方法和研究工具,它推動了各種數學理論的發展。極限計算是高等數學的主要運算,也是高等數學學習的第一個難關,掌握求極限的方法是學好高等數學的基礎。函數極限計算的方法有很多,也非常靈活。每種方法都有它的局限性,下面總結幾種常用的極限計算方法。
1 利用極限的四則運算法則求解

2 利用無窮大與無窮小的關系求解

3 利用無窮小的性質求解
性質 有界函數與無窮小量的乘積是無窮小

4 利用兩個重要極限求解
4.1 第一個重要極限
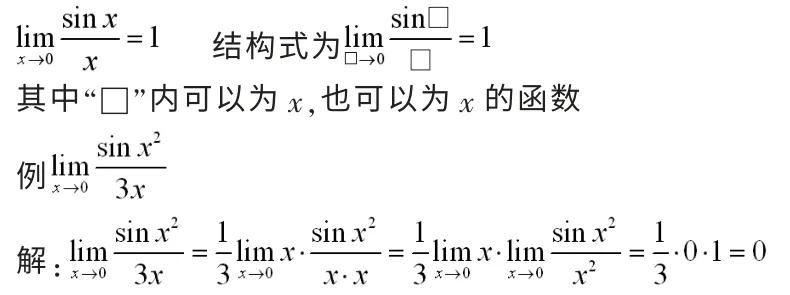
4.2 第二個重要極限
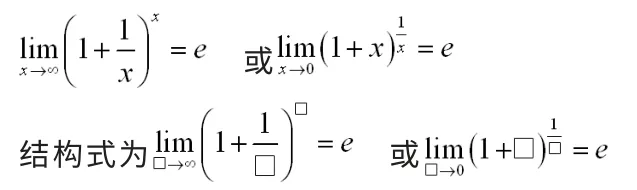
其中“□”內可以為x,也可以為x的函數
利用這個重要公式求這類函數極限,關鍵在于將所給函數湊成公式的形式,然后再利用極限公式求出函數的極限

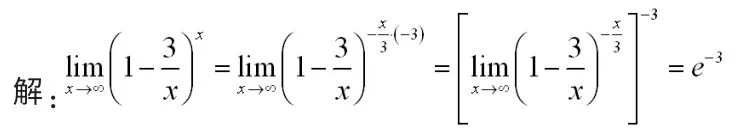
要給學5利用函數連續性求解

解:利用對數的性質,并由復合函數的極限法則
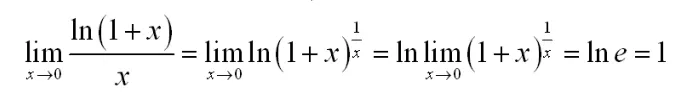
5 利用洛必達法則求解

解:經檢驗為 型
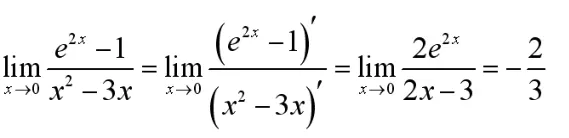
注意:(1)在用此方法求極限之前需先檢驗函數的極限是否為未定型。
(2)洛必達法則可以多次使用,每用一次法則之后,要注意化簡并分析所得式子,直到所求函數不再是未定型為止。
6 利用等價無窮小的代換求解

解:當x→0時,sin 4x~4x,tan 3x~3x
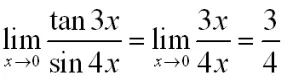
注意:在利用等價無窮小代換求極限時,只能對函數的因子或整體進行無窮小的代換。在分子或分母為和式時,通常不能將和式中的某一項或若干項以其等價無窮小代換。
7 利用左右極限討論分段函數在其分段點處的極限
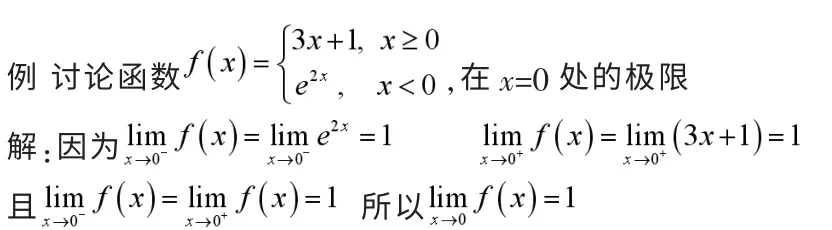
以上8種方法是求函數極限的常用方法,有些題目可能有多種解法,只有不斷地總結和摸索,才能領悟各種方法的精髓,為今后的高等數學的學習奠定良好的基礎。
[1]同濟大學數學系.高等數學[M].6版.北京:高等教育出版社.
[2]吳贛昌.高等數學[M].4版.北京:中國人民大學出版社.
[3]盛祥耀.高等數學輔導(上冊)[M].北京:清華大學大學出版社.
猜你喜歡
中等數學(2022年2期)2022-06-05 07:10:50
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
中等數學(2020年6期)2020-09-21 09:32:38
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
中等數學(2019年6期)2019-08-30 03:41:46
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10
中學生數理化·七年級數學人教版(2018年4期)2018-06-28 03:26:30
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34

