臨床醫學應用定積分數學模型求平均值兩例
趙珍
(河西學院醫學院,甘肅張掖734000)
臨床醫學應用定積分數學模型求平均值兩例
趙珍
(河西學院醫學院,甘肅張掖734000)
現代醫學研究從定性向定量方向發展,高等數學在醫藥學各個分支都有滲透。通過胰島素平均濃度的測定和染料稀釋法測定心輸出量求平均值的兩個實例,說明定積分數學模型的構造方法及步驟,同時也說明在醫學數學化的今天,醫學院校(本科、專科)開設高等數學是十分必要的,不僅培養學生的邏輯思維能力,還培養學生運用數學知識解決醫學問題的能力,為今后從事醫藥科研工作奠定基礎。
臨床醫學;定積分;數學模型
數學是研究現實世界空間形式和數量關系的科學,是量變和質變的表達工具。現代醫學研究由定性向定量方向發展,數學幾乎滲透到了醫藥學各個分支,無論在傳統學科如預防醫學、基礎醫學、臨床醫學還是在邊緣學科如生物醫學工程學、數量遺傳學、藥代動力學、計量診斷學中都有廣泛應用。因此,高等醫學院校開設高等數學是十分必要的[1]。目前一些醫學本科、專科學校對高等數學和醫藥學的關系認識不足,認為開設高等數學沒有必要。本文僅以應用定積分解決臨床醫學兩個實際問題來說明數學在醫學中的廣泛應用。
1 胰島素平均濃度的測定
胰島素是由胰島B細胞受內源性或外源性物質(葡萄糖、乳糖、核糖、精氨酸、胰高血糖素等)刺激而分泌的一種蛋白質激素。胰島素是機體唯一降低血糖的激素,同時促進糖原、脂肪、蛋白質合成。胰島素分為基礎胰島素和餐時胰島素,基礎胰島素是為維持正常空腹血糖水平而分泌的胰島素;餐時胰島素是為了降低餐后升高的血糖、維持餐后正常血糖水平而分泌的胰島素[2]。
1.1 實驗
正常人體空腹血漿胰島素濃度為5~20 U/ml,注射大量葡萄糖30~60分鐘后上升至高峰,高峰值為基礎值的5~10倍,3~4小時后恢復到基礎水平。
先讓病人停服對實驗有影響的藥物3天,調節情緒,禁食一夜以降低血糖水平,然后注射大量葡萄糖,測得空腹、注射后一小時內胰島素濃度,計算病人一小時內血漿胰島素平均濃度。根據一小時內不同時間測得數據,可以得到圖1[3]。
1.2 建立定積分模型
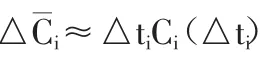
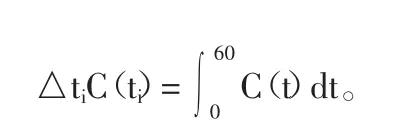
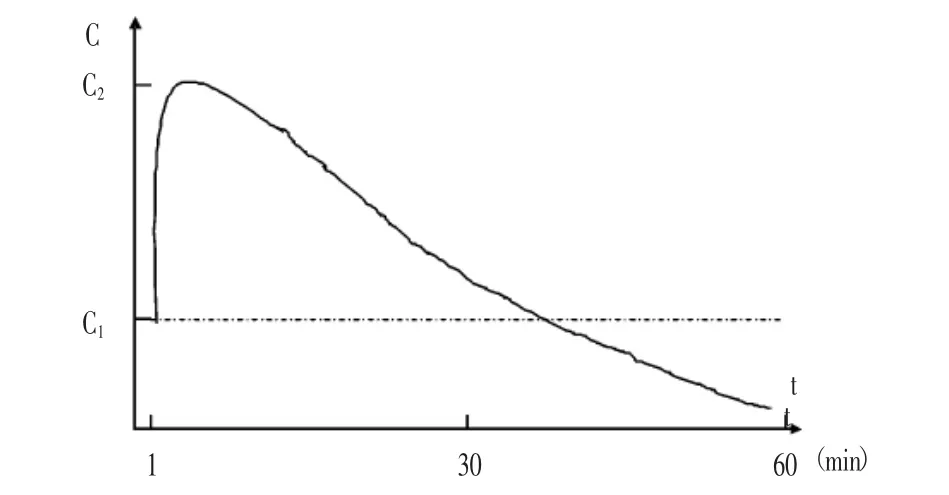
圖1 胰島素時間—濃度曲線
1.3 計算
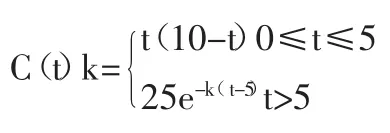
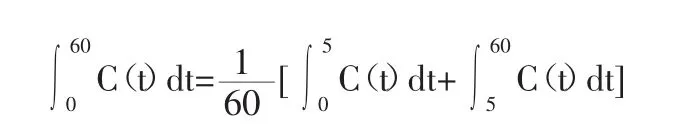
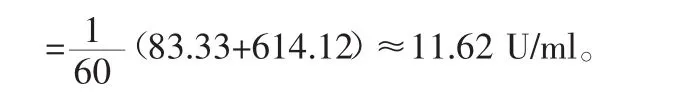
根據計算結果,結合空腹胰島素及一小時內各點分泌情況可做為糖尿病診斷與治療依據。
2 染料稀釋法測定心輸出量
心輸出量是心臟每分鐘射出的血量,是衡量心臟功能的重要指標。心輸出量的測量方法有指示劑稀釋法、阻抗法、超聲、磁共振等。指示劑稀釋法有Fick法、染料稀釋法、熱稀釋法,其測定原理是將一定量的指示劑注射到血液中,經過在血液中的擴散,測定指示劑的變化來計算心輸出量[5]。
2.1 實驗
將5 mg無害、不易透出毛細血管并易于定量的染料注入靜脈,染料與血液混合并隨血液循環通過心臟到達肺部,再返回心臟進入動脈系統,在這個過程中指示劑被稀釋,最后下降至零點。自染料注入后開始在外周動脈中連續測量,測得3秒鐘在動脈血內出現,第9~11秒濃度達峰值,第18秒時濃度降至零點。
根據測量數據,可以得到一條指示劑稀釋的時間—濃度曲線(見圖2)。
2.2 建立定積分模型
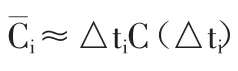
,當分割越細,n→∞時,極限值就越接近真實連續值,即平均濃度近似值和的極限值是30秒內指示劑的平均濃度,這就建立了定積分的數學模型。
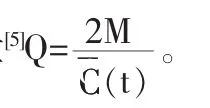

圖2 指示劑稀釋的時間—濃度曲線
2.3 計算
假定30秒內動脈血中染料的濃度和時間的函數關系是[4]

由于該方法較易操作,無需插心導管,也無需測定耗氧量,故用染料稀釋法測定心輸出量,特別是對嬰兒、心臟病病人有著更為廣泛的應用。但染料在血液中是重復循環的,CO計算值有誤差,連續采集血樣測定其血漿濃度操作繁瑣[5]。
以上兩例都是用和的極限求平均值建立定積分數學模型,臨床上用數學方法來解決醫學問題的實例很多,說明數學在醫學中應用廣泛。醫學教育者應認識到數學的價值,既要重視操作能力的培養又不能忽視基礎知識、理論的學習。學習數學能夠培養醫學生的邏輯思維能力、創造性思維,所以醫學院校專科、本科層次各專業開設高等數學課程十分必要。
[1]康曉宇,婁坤.淺談高等數學在現代醫學教育中的作用[J].科技信息,2006(6):234-235.
[2]李經.糖尿病和代謝綜合征的監測與治療[M].北京:中國科學技術出版社,2006.
[3]周人民.談醫學院校高等數學實例教學法的應用[J].科技信息,2009(25):10151.
[4]張選群.醫用高等數學[M].北京:人民衛生出版社,2004.
[5]于金貴,舒雅.各種心輸出量測定方法評價[A].2008年第七次華東六省一市麻醉學學術會議暨浙江省麻醉學術年會論文匯編(上冊)[C].杭州:浙江省科學技術協會,2008.
G421
B
1671-1246(2015)05-0053-02

