資金分配的一個優化模型

任 力，張興芳

（聊城大學a.東昌學院;b.數學科學學院，山東 聊城 252000）

0 引言

有限資金如何分配到有限個單位使其發揮最大效益，是一個重要且復雜的優化問題。某些學者關于這方面已經進行了研究。劉松(1995)[1]引用AHP方法使大學教育經費使用系統建立結構模型尋求可行解及滿意解。蔣紅妍(2008)[2]應用多目標決策理論，針對養護工作中資金及既有養護能力有限的實際,建立了綜合考慮路段特征及不同部門約束條件的資金分配優化模型；彭華(2010)[3]從路網未來高、中、低三種規劃目標出發，提出了瀝青路面網級管理系統中資金優化模型。由Zadeh[4]提出的模糊集理論已歷40余年，其內容已相當豐富，它滲透到數學的許多分支[5～11]，應用領域也相當廣闊，但是將模糊集理論運用到資金分配優化問題中的研究還較少。本文運用模糊集理論構建了一個資金分配問題優化模型，結合高校內部資金分配問題為例證明其有效性。

1 準備知識

為了表述的方便，首先引入折線函數的概念。定義1分段函數

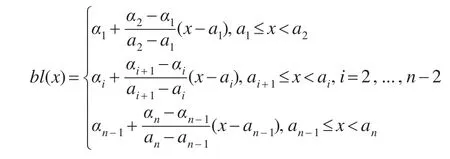
稱為折線函數，簡記作 bl(α1，a1; α2，a2; ...; αn，an)。

性 質 1 設 折 線 函 數 bl1(α1，a1;α2，a2;...;αn，an)，bl2(β1，a1;β2，a2;...;βn，an),則

(1)對任意 aij∈(ai，aj)，有

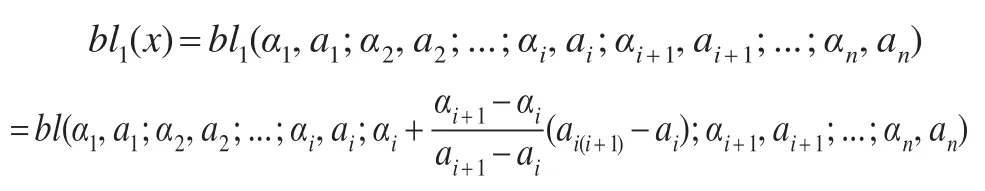
(2)對任意的實數 c1，c2,有

c1× bl1(α1，a1;α2，a2;...;αn，an)± c2× bl2(β1，a1;β2，a2;...;βn，an)=bl1(c1α1±c2β1，a1;c1α2±c2β，a2;...;c1αn±c2βn，an)。

定理1 設 f(x1，x2)=g(x1)×h(x2)，x1+x2=c，g，h 分別在[0,c]遞增。對任意 x1，x2∈[0，c](x1+x2=c)，δ＞0，若

0≤h(x2)-h(x2-δ)≤g(x1+δ)-g(x1)≤h(x2)-g(x1)

則

f(x1+δ，x2-δ)=g(x1+δ)·h(x2-δ)≥g(x1)·h(x2)。

2 一個資金分配的新模型

假設要把有限資金a(a=10h，h是正整數)萬元分配到n個單位。為了讓a萬元在l年內發揮最大效益，一般人們采用下面的方法：先將a萬元分為n個等級

a1，a2，...，an(a1≤ a2≤ ...≤ an，a1+a2+...+an=a)

且確定分配的依據，假設從 w1，w2，...，wh方面進行評價。然后由專家根據這h個方面綜合打分或投票排出名次，從而確定分配方案。顯然，這種方法太粗糙，目標不明確。下面運用模糊集理論處理該問題。

首先將每個單位的 h 個方面 w1，w2，...，wh的績效分別視為一個論域為[0，a]的模糊集。假設第i(i=1，2，...，n)個單位對應 wj方面的模糊集為

uij(x)(i=1，2，...，n;j=1，2，...，h)。

uij(x0)(i=1，2，...，n;j=1，2，...，h)的意義是第 i個單位在u年末資金x0產生wj的效益程度。然而，過去并不代表將來，還要由專家基于各部門的實際情況預測投資l年末的各指標的發展前景，從而確定其隸屬函數。隸屬函數的確定有兩種方法。一種是先將歷史數據模糊化然后模糊推理得到；第二種是由專家評價給出。下面僅討論第二種方法：專家評價法。

首先根據發展不均衡的原則，由專家確定暫緩發展對象及重點培養對象，分別稱它們為第1單位，第2單位，…，第m（m＜n)單位，并確定它們分配的資金數，假設為a1，a2，...，am（a1＜a2＜...＜am＜a）。然后，由專家分別賦予其余部門近 l年末 w1，w2，...，wh的水平達到最大值 α（≤1）所需要的花費，并分別賦予其權重，設為 q1，q2，...，qh。然后再分別擴張它們為一個在 [0，c]，c=max{a1，a2，...，am}＜a上不減的折線函數，分別稱它們為 w1，w2，...，wh的資金效益函數（具體擴張方法見下一節的實例）。假設第i個單位 關 于 wj的 資 金 效 益 函 數 為 μij(xi)，xi∈[0，c]i=m+1，...，n ，j=1，2，...，h 。于是建立下面的資金分配模型：

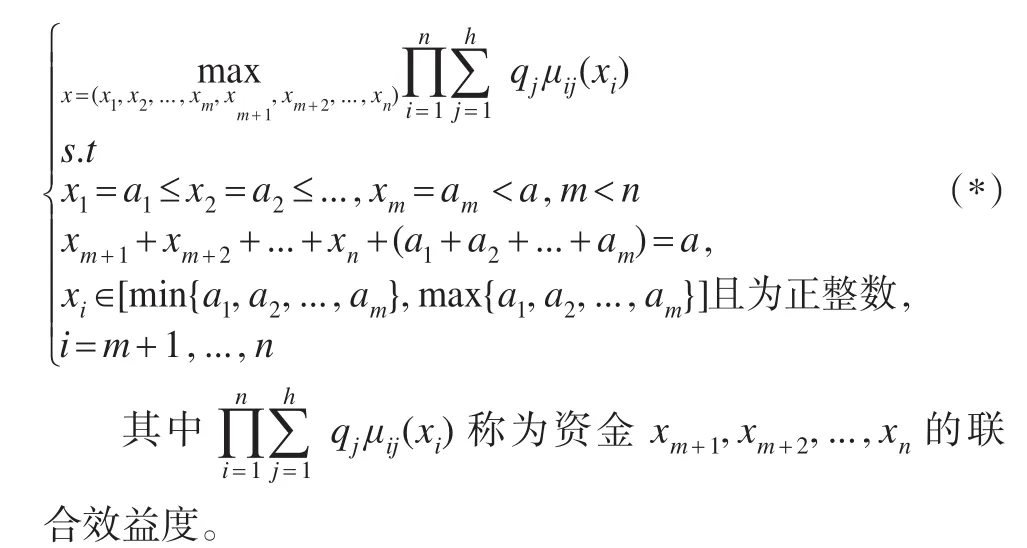
該模型中的條件

min{a1，a2，...，am}≤ xi≤ max{a1，a2，...，am}，i=m+1，...，n

說明資金分配方案隨著中間水平的部門的分配方案的確定而確定。

3 以高校內部資金分配問題為例的模型

本文假設某一高校要把資金300萬元分配到10個部門，以作為它們近3年內的發展經費。

（1）將高等教育三大職能——科學研究、人才培養、服務社會在資金分配問題中賦予不同權重，分別記為w1，w2，w3。設定w1，w2，w3的權重為0.4，0.4，0.2。

(2)根據培植強勢，不均衡發展的原則，專家評定第1單位和第2單位為暫緩發展單位，第3單位，第4單位和第5單位為3個重點扶持單位，并確定分配它們的資金為10萬元，15萬元，40萬元,50萬元，60萬元。

(3)分別確定第6單位,第7單位,第8單位,第9單位,第10單位關于 w1，w2，w3的效益函數。

假設w1的資金效益函數分別為

μ61(0，0;0.5，15;0.9，60)，μ71(0，0;0.5，20;085，60)，

μ81(0，0;0.5，25;0.8，60)，μ91(0，0;，0.5，25;0.70，60)，

μ(10)1(0，0;0.5，30;0.70，60)。

如圖所示：

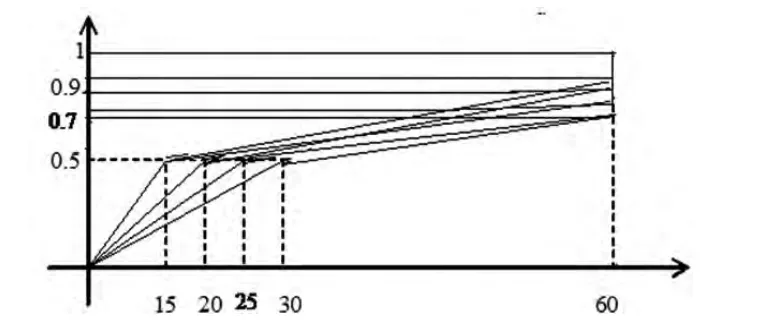
又假設w2的資金效益函數分別為

μ62(0，0;0.5，35;1，60)，μ72(0，0;0.5，30;085，60)，

μ82(0，0;0.5，20;0.9，60)，μ92(0，0;，0.5，20;0.75，60)，

μ(10)2(0，0;0.5，20;0.75，60)

w3的資金效益函數分別為

μ63(0，0;0.5，35;0.7，60)，μ73(0，0;0.5，40;055，60)，

μ83(0，0;0.5，45;0.6，60)，μ93(0，0;，0.5，45;0.6，60)，

μ(10)3(0，0;0.5，40;0.7，60)。

根據性質1，有

μ61(0，0;0.5，15;0.9，60)

=μ61(0，0;0.5，15;0.68，35;0.9，60)

μ62(0，0;0.5，35;1，60)

=μ62(0，0;0.75，15;0.5，35;1，60)

μ63(0，0;0.5，35;0.7，60)

=μ63(0，0;0.21，15;0.5，35;0.7，60)

μ71(0，0;0.5，20;085，60)

=(0，0;0.5，15;0.59，30;0.68，40;085，60)

μ72(0，0;0.5，30;085，60)

=μ72(0，0;0.33，15;0.5，30;0.62，40;085，60)

μ73(0，0;0.5，40;0.55，60)

=μ73(0，0;0.25，15;0.38，30;0.5，40;0.55，60)

μ81(0，0;0.5，25;0.8，60)

=μ81(0，0;0.4，20;0.5，25;0.63，45;0.8，60)

μ82(0，0;0.5，20;0.9，60)

=μ82(0，0;0.5，20;0.55，25;0.75，45;0.9，60)

μ83(0，0;0.5，45;0.6，60)

=μ83(0，0;0.22，20;0.28，25;0.5，45;0.6，60)

μ91(0，0;，0.5，25;0.70，60)

=μ91(0，0;0.4，20;0.5，25;0.59，40;0.70，60)

μ92(0，0;，0.5，20;0.75，60)

=μ92(0，0;，0.5，20;0.53，25;0.63，40;0.75，60)

μ93(0，0;，0.5，45;0.6，60)

=μ93(0，0;0.22，20;0.27，25;0.5，40;0.6，60)

μ(10)1(0，0;0.5，30;0.70，60)

=μ(10)1(0，0;0.33，20;0.5，30;0.56，40;0.70，60)

μ(10)2(0，0;0.5，20;0.75，60)

=μ(10)2(0，0;0.5，20;0.56，30;0.63，40;0.75，60)

μ(10)3(0，0;0.5，40;0.7，60)

=μ(10)3(0，0;0.25，20;0.38，30;0.5，40;0.7，60)

根 據 公 式 ti(xi)=0.4μi1(xi)+0.4μi2(xi)+0.2μi3(xi)，i=6，7，8，9，10與性質1，有

t6(x6)=μ6(0，0;0.542，15;0.572，35;0.9，60)

=μ6(0，0;0.542，15;0.5495;20;0.5570，25;0.5645，30;

0.572 ，35;0.6376，40;0.7032，45;0.9，60)，

t7(x7)=μ7(0，0;0.382，15;0.512，30;0.620，40;0.88，60)

=μ7(0，0，0.382，15，0.4253，20;0.4687，25;0.512，30;

0.566 ，35;0.620，40;0.685，45;0.88，60)，

t8(x8)=μ8(0，0;15;0.404，20;0.476，25;30;35;40;

0.652 ，45;0.80，60)

=μ8(0，0;0.404，15;0.44，20;0.476，25;0.52，30;0.564，35;0.652，40;0.608，45;0.80，60)，

t9(x9)=μ9(0，0;15;0.404，20;0.466，25;30;35;0.588，40;45;0.70，60)

=μ9(0，0;0.404，15;0.435，20;0.466，25;0.5067，30;0.5473，

35;0.588，40;0.616，45;0.70，60)，

t10(x8)=μ10(0，0;0.382，20;0.50，30;0.576，40;0.72，60)=μ10(0，0;0.382，15;0.4115，20;0.441，25;0.50，30;0.538，

35;0.576，40;0.612，45;0.72，60).

于是，構建高校內部資金分配的一個優化模型如下：

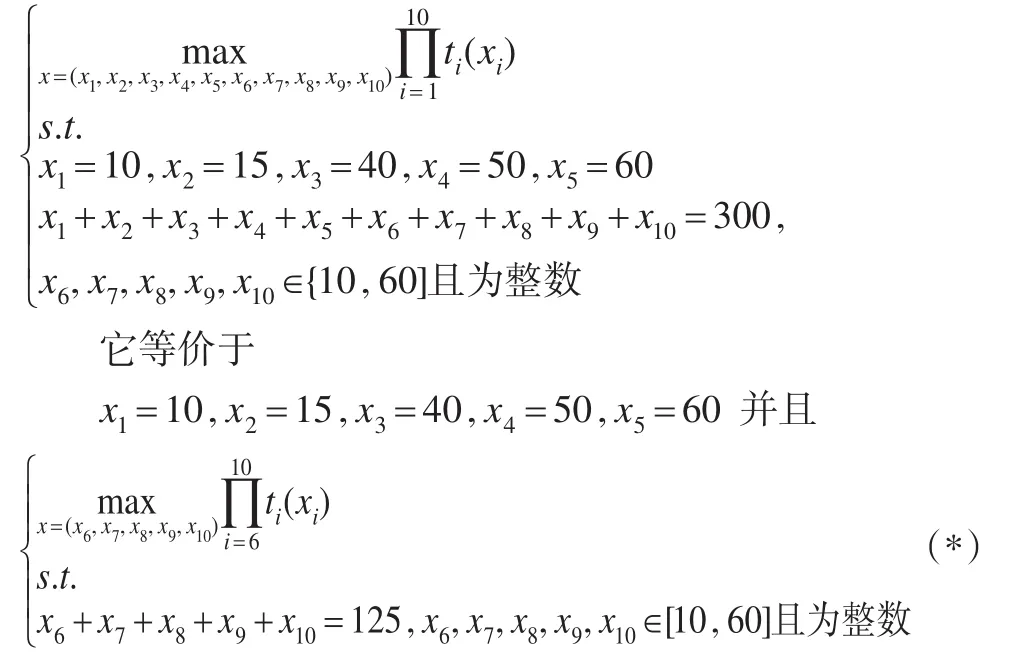
通過模型（*）的一個人機對話算法（算法略）,得到模型（*）的解為 x=(10,15,40,50,60,15,25,26,23,34)。

4 結論

本文基于模糊集理論提出了一個資金分配的優化新模型，并以高校資金分配為例展現了這種模型的有效性。

[1]劉松.高校資金使用結構及其優化設計模型[J].沈陽工業大學學報,1995,(2).

[2]蔣紅妍.基于多目標決策的養護資金分配優化模型及應用[J].公路工程,2008,(3).

[3]彭華,孫立軍,陳長.瀝青路面網級管理系統中資金優化模型[J].同濟大學學報(自然科學版),2010,(8).

[4]Zadeh L A.Fuzzy sets,Information and Control[J].1965，(8).

[5]李洪興.Fuzzy系統的概率表示[J].中國科學（E）信息科學,2006，36（4）.

[6]孟廣武.層次L-拓撲空間論[M].北京:科學出版社,2010.