模態正交性及其對角化功能
劉國松,張 淼
(長春工程學院理學院,吉林長春 130012)
模態正交性及其對角化功能
劉國松,張 淼
(長春工程學院理學院,吉林長春 130012)
本文針對目前常用的各種阻尼系統的模態向量的正交性進行了分類及評述,對它們所能實現的對角化功能進行了辨析,通過對比和分析它們的使用條件和范圍以及使用過程中需要注意的問題,為工程應用提供了良好的理論基礎。
阻尼系統;正交性;對角化;標號現象;狀態方程
解耦的目的是將一組方程變成相互獨立的單個方程,從而解出所需的多維未知向量。矩陣的對角化,在工程應用中往往對應著某種類型方程的解耦。例如,振動方程可以通過振型向量進行解耦,事實上這種解耦實現的就是系統性質矩陣的角化[1],如果對角化難以實現,振動方程的解耦就更難以實現了。再則,靈敏度系數控制方程的解耦[2]也是通過將狀態矩陣或性質矩陣對稱化來完成的。可見對角化功能的實現是一個非常重要的前提,而它所依賴的基礎則是系統本身擁有的無阻尼實模態參數或阻尼復模態參數的正交性。不同的系統,這些模態參數的正交性可能完整,也可能缺失[3-4],因此針對不同的系統結構,應考慮合理且靈活地使用系統模態參數,這是解決工程問題非常重要的前提。
1 實模態參數
描述自由度為N的線性阻尼離散系統的自由振動方程為
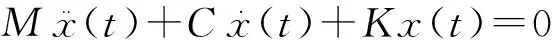
(1)
相應地,其強迫振動方程為

(2)


(3)
設每個實模態的正則化系數為ai,即
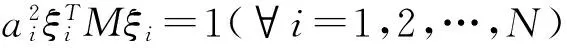
(4)
記aiξi=vi,稱為無阻尼正則固有振型,簡稱為振型,則V=[v1,…,vN]為振型矩陣。
1.1 單頻且對稱系統的模態正交性及對角化功能
如果K,M為對稱陣,且實頻率全不相同,那么此時振型矩陣可以角化質量和剛度矩陣[5],如下
VTMV=E.
(5)
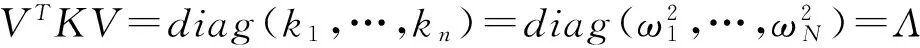
(6)
也就是說,振型關于質量和剛度陣是加權正交的。如果此時的振型剛好能對角化阻尼矩陣,那么系統(1)和(2)稱為經典阻尼系統[6],即
VTCV=diag(c1,…,cN).
(7)
振型關于阻尼陣也是加權正交的。否則稱為非經典阻尼系統[7],顯然對非經典阻尼系統而言,振型并不能對角化阻尼矩陣。
1.2 重頻或非對稱系統的模態正交性及對角化功能
如果K,M為非對稱矩陣,或者實頻率發生重復,那么(5)和(6)式不再成立[8],此時先將(3)式化為如下形式
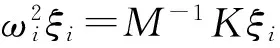
記M-1K=D,上式化為
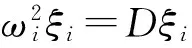
(8)
我們可以說,(8)式中的矩陣D的特征值和特征向量,即為(3)式中的矩陣K,M的廣義特征值和廣義特征向量,也是(1)式對應的無阻尼系統的實頻率和實模態。此時D一般為非對稱矩陣,或其特征值發生重復,其特征向量系并不能保證正交性[8],因此對角化并不容易實現。設其特征向量系雖然不能保證正交性,但具有無關性,即可引入伴隨向量來實現正交性及對角化功能。設V=[v1,…,vN]的伴隨向量系為Z=[z1,…,zN],則有
ZTV=E.
(9)
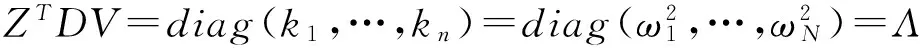
(10)
這里有兩個問題需要注意,一是要注意標號現象的出現,例如按(5)式所示,應該有
2 復模態參數
考慮阻尼時的系統極點及復模態對(λi,ui)(i=1,2,…,2N),滿足方程

對于N自由度振動系統,特征方程det[λ2M+λC+K]=0有2N個呈復共軛對出現的特征值λ1,λ2,…,λ2N(其中λi+1為λi的共軛(i=1,3,…,2N-1)),稱為系統的極點。這些頻率對應著一組呈復共軛對出現特征向量ui∈CN稱為系統(1)與λi相對應的第i個模態向量。將u1,u2,…,u2N(其中ui+1為ui的共軛(i=1,3,…,2N-1)),稱為復模態。這些復模態不能對角化任何一個性質矩陣M,C,K,但它們所構成的狀態向量,在狀態空間中可以對角化狀態矩陣,仍然可以實現對角化功能,除了由N維空間拓展至2N維空間所帶來的麻煩外,基本不妨礙對角化功能的應用。
2.1 單頻且對稱系統的模態正交性及對角化功能
如果K,C,M均為對稱陣,且復頻率全不相同,那么構造狀態向量φi=[uiλiui]T(i=1,2,…,2N),則有狀態方程為
(λiA+B)φi=0.
(11)
ΦTAΦ=E.
(12)
ΦTBΦ=diag(-λ1,…,-λ2N).
(13)
2.2 重頻或非對稱系統的模態正交性及對角化功能
如果K,C,M至少有一個為非對稱陣,或復頻率發生重復,那么(12)和(13)式不再成立,但此時狀態向量不變,而使用狀態方程變為
λiφi=Hφi.
(14)
ΨTΦ=E.
(15)
ΨTHΦ=diag(-λ1,…,-λ2N).
(16)
需要說明的是,復模態參數的標號現象[9]可能更為常見,也如前文所述的方法加以處理,即可實現正交(15)和(16)式,使標號現象并不致妨礙對角化功能的應用。
如果當K,C,M均對稱,且系統復頻率發生重復時,也可以使用(λiA+B)φi=0型狀態方程,但它的狀態向量可能并不正交,主要是因為那些重頻所對應的狀態向量之間可能并不具有正交性,因此需要實施施密特正交化技術,才能使它們完全具有正交性,再繼續實現對角化功能[12]。
如果當K,C,M非對稱,且系統具有重頻時,即使是不同頻率所對應狀態向量也不能保證正交性,如果如文獻[13]那樣,引入左狀態向量,也只能保證不同頻率所對應的左右狀態向量之間是正交的。只能如上述2.2小節中所指出的那樣,引入伴隨向量系來實現對角化功能。
[1]張淼,于瀾,鞠偉.基于頻響函數矩陣計算阻尼系統動力響應的新方法[J].振動與沖擊,2014,33(4):161-166.
[2]張淼,于瀾,鞠偉.重頻系統的頻率靈敏度分析算法研究[J].華南師范大學學報:自然科學版,2014,46(3):40-44.
[3]張淼,于瀾,鞠偉.虧損振系廣義狀態向量靈敏度的移頻算法[J].計算力學學報,2013,30(6):872-878.
[4]張淼.虧損結構振動方程的穩態響應求解[J].吉林師范大學學報:自然科學版,2014,35(1):91-94.
[5]李德葆,陸秋海.實驗模態分析及其應用[M].北京:科學出版社,2001.
[6]張淼,于瀾.對稱經典阻尼系統動力響應精確算法的比較研究[J].吉林師范大學學報:自然科學版,2015,36(1):99-103.
[7]張淼,于瀾.對稱非經典阻尼系統動力響應精確算法比較[J].長春工業大學學報:自然科學版,2015,36(1):107-110.
[8]方保镕,周繼東,李醫民.矩陣論[M].北京:清華大學出版社,2004:146-147.
[9]張淼,于瀾,鞠偉.復模態正交性理論的異常現象及對策分析[J].應用數學和力學,2014,35(10):1081-1091.
[10]張文丹.對稱結構復模態向量的二階泰勒展開[J].長春理工大學學報,2014,37(6):142-146.
[11]張淼.非對稱結構振型向量的海森陣算法及應用研究[J].長春工業大學學報:自然科學版,2014,35(2):216-220.
[12]張淼,于瀾,鞠偉.重頻結構模態靈敏度分析的高精度截模態算法[J].振動工程學報,2014,27(4):526-532.
[13]于瀾,張淼,鞠偉,等.非保守系統復模態的規范正交性及其應用[J].華南師范大學學報:自然科學版,2013,45(4): 21-24.
Orthogonality of Modes and Its Diagonalization Function
LIU Guo-song,ZHANG Miao
(Changchun Institute of Technology, Changchun Jilin 130012, China)
For the sake of several usual damping systems, the orthogonality of modes are remarked and sorted.The diagonalization function which they can carry out is differentiated and analyzed. And it applies the favorable theories by comparing conditions and range.
damped system; orthogonality; diagonalization; label phenomenon; state-space equation
2015-07-09
吉林省教育廳資助項目(吉教科合字[2014]335);長春工程學院種子基金項目(320140026)。
劉國松(1979- ),男,吉林長春人,長春工程學院理學院副教授,碩士,從事理論物理及實驗研究。
O321;TB122
A
2095-7602(2015)12-0005-03

