基于進化動力學的企業創新模型研究

○班曉倩

（貴州財經大學數學與統計學院 貴州 貴陽 550025）

基于進化動力學的企業創新模型研究

○班曉倩

（貴州財經大學數學與統計學院 貴州 貴陽 550025）

本文建立于進化動力學理論基礎之上，引入創新系數和滯后系數，分別討論了企業晉級模型和企業晉級—降級模型，運用微分方程穩定性理論分析了其穩定性，并進行了數值仿真。結果表明，模型有效模擬了企業創新的動態演化過程。

企業競爭 晉級模型 晉級—降級模型

一、引言

近年來，許多學者嘗試利用生態系統中的種群間競爭分析經濟系統中的企業競爭，得到了良好的結論。幾乎所有這方面的論文都是利用生物數學中經典的 Lotka-Volterra方程對企業行為進行分析，這些研究是富有成效的，但是既然企業間的競爭和合作都是動態的，那么從生物進化動力學的角度分析企業間競爭和合作將是非常貼合實際的。因此，下面我們嘗試利用進化動力學的思想方法，構造企業創新動態演化發展模型，并對模型進行分析。希望我們的工作對于當前的研究有所補充。

假設A，B為某一種群的兩個亞種，考慮到生態系統中總是存在最大容量，因此下面我們假設兩個亞種總的數量保持不變。X1，X2為這兩個亞種在某時刻的相對多度（即比例），那么必然有X1+X2=1。根據進化動力學理論，建立如下的選擇動力學方程：

其中，a，b為兩個亞種的適合度（即繁殖率），φ=aX1+bX2為兩個亞種的平均適合度。顯然A，B兩個亞種的適合度決定了它們的未來：如果某亞種的適合度超出平均適合度，則該亞種的相對多度將持續增加，換句話說，另外一個亞種可能面臨被淘汰的命運；當滿足一定的條件時，兩個亞種也可能實現某種形式的穩定共存。

企業在面對激烈的市場競爭時，如果沒有周期性的有計劃的創新決策，就很難創造企業新的核心能力，就會使企業在激烈的市場競爭中處于被動的局面，就會使企業內部失去生存與發展的動力。但是，由于創新需要沖破原有的企業結構和思想觀念，需要追加高額的風險投資成本，因而許多企業會因為惰性而不愿意進行創新。于是，我們可以將市場上生產同一產品的企業視為同一種群的兩個亞種，其中的一個亞種屬于技術創新型企業，另一個亞種屬于落后淘汰型企業。基于以上討論，可以利用進化動力學對企業間的動態發展進行分析，從而可以建立如下企業創新動態演化模型。

二、模型和分析

1、晉級模型

假設在某一市場上生產同一產品的企業分為兩類：一類為技術創新型企業，另一類為落后淘汰型的企業。考慮到技術革新性企業往往污染小、社會效益好，所以往往能夠得到國家政策的支持；而那些落后淘汰型企業往往因為環境污染大、社會效益差，屬于國家要求停產關閉的對象，因此要保持生存，必然要求它們不斷改進生產工藝，于是有一部分落后淘汰型企業會向技術創新型企業轉變。考慮到市場存在最大的飽和量，因此我們總假設市場上生產該產品的企業數量保持不變，基于以上的考慮，我們得到如下的模型：

其中，X1為技術創新型企業的相對多度（即比例），X2為落后淘汰型企業的相對多度，且滿足X1+X2=1；φ為兩類企業的平均適合度，φ=aX1+bX2；a為技術創新型企業的適合度，b為落后淘汰型企業的適合度，因為落后淘汰型企業的所需成本低，更易擴張，因此我們假設a＜b；假設μ為落后淘汰型企業向技術創新型企業轉變的系數，且稱0＜μ＜1為創新系數。如果我們將淘汰落后型企業轉變為技術創新型企業稱作“晉級”，那么我們稱系統（2）為企業晉級模型。

下面利用微分方程定性理論，求解系統（2）的平衡點。由φ=aX1+bX2及X1+X2=1，容易得到φ=aX1+bX2=b+（a-b）X1，將其代入系統（2），并令

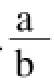
2、晉級—降級模型

晉級模型（2）刻畫了落后淘汰型企業和技術創新型企業的動態競爭過程，但是此處暗含了技術創新型企業一直保持良好的技術創新狀態。然而，從較長的周期來看，兩類企業的狀態應當是相對的、動態的。事實上，許多企業在企業生命周期的成熟期，整個企業處于惰性狀態，缺少創新所需的內部條件，因此技術創新型企業也同樣可能會轉變成落后淘汰型企業。在實際觀察中，我們也不乏這樣的案例。所以，在建立模型時需要考慮這一因素，即我們需要考慮技術創新型企業和落后淘汰型企業相互轉變的可能性。仿照之前的分析，我們稱技術創新型企業轉變為落后淘汰型企業的過程稱為“降級”。

顯然，技術創新型企業相對多度的變化率就應當等于落后淘汰型企業的晉級率減去技術創新型企業的降級率。因此，在對晉級模型（2）進行修正后，我們得到了如下的企業晉級—降級模型：

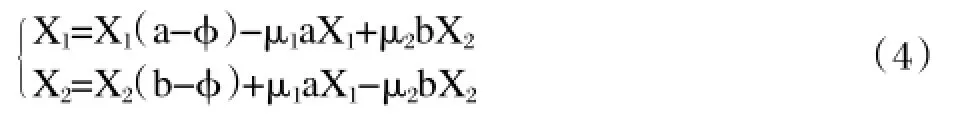
其中，μ1為技術創新型企業向落后淘汰型企業轉變的系數，稱0＜μ1＜1為落后系數；μ2為落后淘汰型企業向技術創新型企業轉變的系數，即創新系數且滿足0＜μ2＜1。其余變量和參數的意義均與系統（2）保持一致。

同樣利用微分方程定性理論，求解系統（4）的平衡點。令

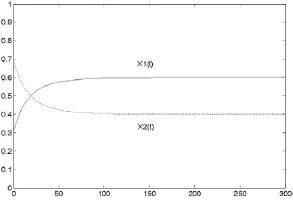
圖1 μ=0．2時，——X1（t）的曲線，— —X2（t）的曲線

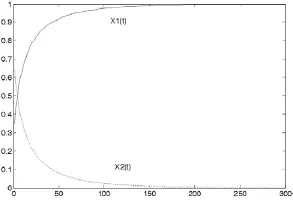
圖2 μ=0．4時，——X1（t）的曲線，— —X2（t）的曲線

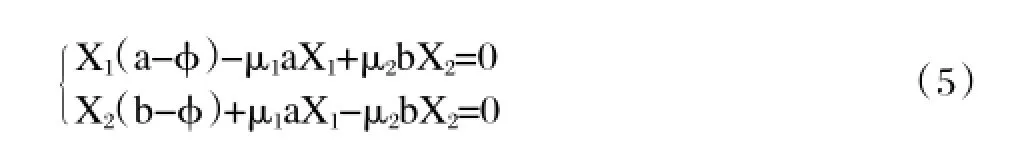
由φ=aX1+bX2及X1+X2=1，得到φ=aX1+bX2=b+（a-b）X1，代入方程（5），得（b-a）X21+（a-b-μ1a-μ2b）X1+μ2b=0，解得

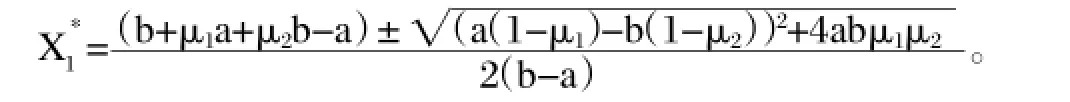
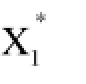
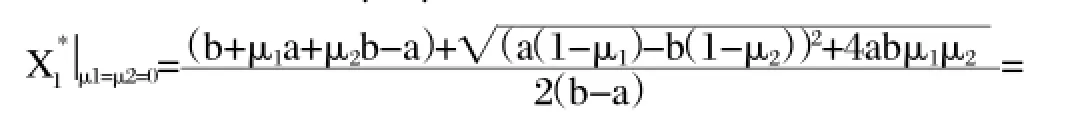
對于企業晉級—降級模型（4），顯然有

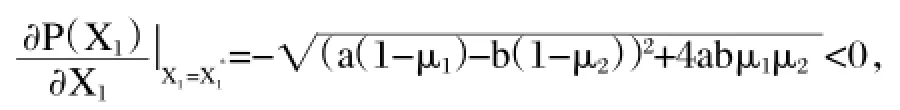
這說明X*1是穩定正平衡點。此時

于是我們得到如下的結論。

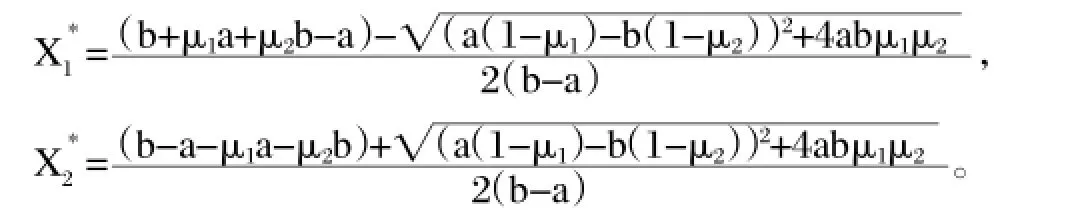
定理2說明，無論兩類企業在初始狀態下的相對多度是多少，最終兩類企業的相對多度X1和X2一定會達到穩定的狀態，即兩類企業的比例保持穩定不變。

三、數值仿真與分析

1、例1

對于晉級模型（2），考慮X1（0）=0.3，X2（0）=0.7，a=0.2，b=0.3，可得到如下系統：

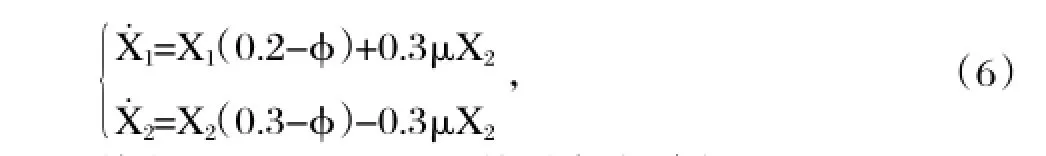
其中φ=0.2X1+0.3X2。然后在分別取μ=0.2和μ=0.4，得到數值仿真圖1和圖2。

2、例2

對于晉級—降級模型（4），考慮X1（0）=0.3，X2（0）=0. 7，a=0.2，b=0.3，μ1=0.1，μ2=0.25，可得到如下系統：其中φ=0.2X1+0.3X2，得到數值仿真圖3。

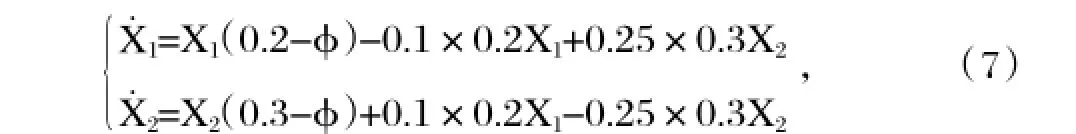
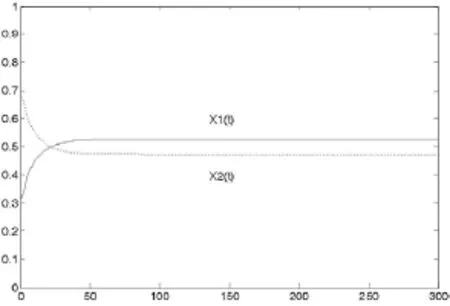
圖3 μ1=0．1，μ2=0．25時，——X1（t）的曲線，— —X2（t）的曲線

從圖3可以看出，X1（t）和X2（t）最終都趨于穩定平衡解。這意味著，隨著時間的推移，技術創新型企業和落后淘汰型企業的比例最終將趨于穩定。

四、討論

（注：基金項目：2014年度貴州財經大學教學質量與教學改革項目。）

[1]袁桂秋：企業投資活動中模仿學習行為的經濟學解釋[J]．生物數學學報，2009，24（1）．

[2]姚奕：基于生態競爭方程的企業競爭動態演化研究[J]．經濟數學，2011，28（2）．

[3]賈慶菊、馮文俊、楊建中：企業受金融危機影響的數學模型[J]．數學的實踐與認識，2011，18（9）．

[4]周浩：企業集群的共生模型及穩定性分析[J]．系統工程，2003，21（4）．

[5]陳金波：企業競爭的進化博弈論與種群生態學模型[J]．數學的實踐與認識，2009，39（1）．

[6]張睿、錢省三、高臻：基于生態學理論的企業競爭模型[J]．系統工程，2008，26（2）．

[7]Martin A．Nowak．：Evolutionary dynamics，exploring the equations of life[M]．Harvard University Press，London，2006．

[8]Christine Taylor，et al．：Evolutionary game dynamics in finite populations[J]．Bulletin of Mathematical Biology，2004（66）．

（責任編輯：胡婉君）