粒子群優化在甲狀腺結節特征選擇中的應用

李 毅,李 晶，陸永萍，黃紅兵

甲狀腺結節是一種高發病，早期發現并鑒別其良惡性對臨床治療及手術選擇有重要意義。甲狀腺結節診斷首選的方法是超聲影像檢查[1]，影像醫生依據自身經驗，通過考察結節大小、質地、形狀、邊界和彈性等特征來鑒別其良惡性[2]。 這種特征選擇有強烈的主觀因素，缺乏量化標準，也不能更深入地分析細微的紋理特征。 因此，本研究使用數字圖像技術提取了77 個甲狀腺結節超聲圖像特征。 然而，由于甲狀腺結節超聲圖像的特征繁多，各特征間存在冗余性，因此，需要使用特征選擇方法，提取最優特征子集，以降低特征維度，節省分類器的訓練時間，提高分類識別性能，更好地理解關鍵特征[3]。本研究引入粒子群優化[4]進行特征選擇，獲得了理想的實驗結果，并據此構建了甲狀腺結節良惡性風險評估計算機輔助診斷系統。

1 甲狀腺結節超聲圖像特征提取

1.1 影像資料 2009 年6 月～2014 年12 月因甲狀腺結節性疾病來云南省第二人民醫院就診的患者共計31 654 例，均行超聲成像檢查。 檢查設備為法 國 聲 科 影 像 公 司 （SuperSonic Imagine） 的AixplorerR新聲威特種鑒別診斷超聲系統， 探頭為SL15-4，增益及二維條件固定。 在這些病例中，提交病理檢查且有電子存檔的患者共93 例， 其中惡性18 例，男14 例，年齡25～85 歲，平均54 歲，共1334張超聲結節影像。 根據結節視野的清晰程度，從中篩選得到245 張圖像，如圖1 示例。

1.2 形態特征 計算結節的周長C ，面積A ，質心O 到邊緣的距離Ri，i ∈[1,C]，Ri的均值R 、熵H(Ri) (F1)和標準差δ (F2)。 對結節進行凸包運算，得到凸包的周長CH和面積AH。進而計算結節的緊致度com(F3)、圓形度cir (F4)、平滑度smo (F5)、凹凸性cc(F6)、不規則度irr(F7)和輪廓溫度HT (F8)：

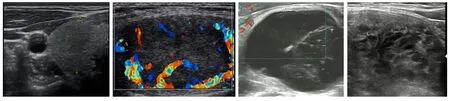
圖1 超聲結節影像示例

計算結節邊緣每個像素的曲率Ki，i ∈[1,C] ，得到曲率熵H(Ki) (F9)，由公式（7）計算將直線彎曲成特定曲線形狀所需要的能量，即彎曲能KE (F10)。

1.3 紋理特征 （1）基礎統計：灰度均值(F11)、標準差(F12)、平均能量(F13)和熵(F14)。 （2）灰度直方圖：二階矩(F15)、三階矩(F15)和四階矩(F16)。 （3）灰度梯度直方圖：對比度(F17)、熵(F18)和均值(F19)。（4）灰度共生矩陣[5]：均值(F20)、方差(F21)、逆差矩(F22)、對比度(F23)、熵(F24)、角二階矩（能量）(F25)和相關性(F26)。 （5）Laws 紋理能量測度[6]：通過特定的2D 算子核與原始圖像卷積來表達紋理標記，即灰度級L 、邊緣E 、點S、波W 和紋R 五個算子分別完成一維信號的灰度平滑、邊緣檢測、點檢測、波狀檢測和紋狀檢測，從中選取LE 均值(F27)、 EL 均值(F28)、 SL 均值(F29)、 EE 均值(F30)、 LS 均值(F31)、 LE 方差(F32)、 EL 方差(F33)、 SL 方差(F34)、EE 方差(F35)、 LS 方差(F36)。 （6）灰度游程矩陣[7]用于描述紋理基元，定義為具有相同灰度值的最大共線連接的像素集合： 短游程逆矩(F37)、 長游程矩(F38)、灰度不均勻性(F39)和長度不均勻性(F40)。（7）分形維度方法基于分形幾何中的自相似性對紋理的尺度特征經行度量，分形維越大，紋理越粗糙。使用盒子維法[8]計算分形維度量(F41)。（8）局部二值模式是描述圖像局部空間結構的非參數算子，本研究使用多尺度一致編碼LBP 算子(F42)[9]。 （9）Gabor變換[10]作為一種短時傅里葉變換，是圖像時域-頻域分析的基礎，其中心頻率(F43)的差別可反映出紋理所具有的準周期性特性。 （10） 局部傅里葉變換[11]， 選取極坐標下8 個方向數量積的均值(F44-F52)和方差(F53-F60)，8 個方向相角的均值(F61-F68)和方差(F69-F77)。

2 基于粒子群優化的特征選擇方法

2.1 特征選擇 特征選擇[3]本質上是一個組合優化問題[12]，即尋求最優化子集以提高分類器的識別能力和效率。 在搜索特征子集時，可以使用粒子群優化提升搜索效率。

2.2 粒子群優化 在鳥群聚和覓食行為的啟發下，Eberhart 和Kennedy 提出了最早的粒子群算法(particle swarm optimization, PSO )[4]。 假設在一個D維的目標搜索空間中，有m 個粒子組成的群落，其中第i 個粒子表示為一個D 維的向量xi=(xi1,xi2,...,xiD)T，i =1,2,...,m， 即第i 個粒子在D 的搜索空間中的位置是xi。 將xi代入目標函數計算其適應度值，其歷史最優值記為pi=(pi1,pi2,...,piD)T，群落的歷史最優位置為pg=(pg1,pg2,...,pgD)T。 同時，賦予第i 個粒子一個速度，記為vi=(vi1,vi2,...,viD)T。

為了解決組合優化問題， 離散二進制粒子群（binary barticle swarm optimization, BPSO）[13]采用下列公式，在每一代k 中對粒子的位置和速度進行更新：

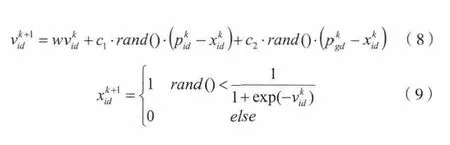
其中w 為慣性因子，表示粒子當前速度對下一代速度的影響權重。 c1和c2為加速因子，表示粒子自身和群體運動的加速度，分別構成"認知"和"社會"部分， 是位于[0,1]之間的隨機數。

2.3 算法參數 特征總數即維度D，粒子可以表示為一個長度為D 的二進制串， 每一位即代表一個特征，為1 則該特征被選中，為0 則沒有被選中。

特征選擇需要考慮特征數目和分類精度兩個重要指標，采用下列方法作為適應度函數[4]：

其中， A(xi)表示以xi所表征的特征子集進行分類的精度，本研究采用留一交叉檢驗法[14]評價分類精度。 N(xi) 即xi所表征的特征子集的特征數目。

2.4 算法步驟 （1） 初始化： 設定最大迭代數Gmax、適應度閾值F(xi)max等參數值，隨機生成粒子群， 并隨機設置每個粒子的位置xi0和速度vi0，并初始化各粒子的p0id和p0gd種群的；（2） 根據適應度函數（公式10）計算粒子的適應度值F(xik) ；（3）根據（公式8 和9）更新粒子的位置xik和速度vik；（4）更新各粒子的pKid和種群的pkgd；（5）判斷退出條件：達到最大迭代數Gmax，或找到超過適應度閾值F(xi)max的特征子集。滿足則輸出最優結果，不滿足則重復（3）（4）。

3 實驗結果與分析

3.1 特征選擇方法的比較 本研究對上述提取的77 個特征（F1～77）分別施用BPSO 和Relief[15]特征選擇方法，使用支持向量機[16]分類（表1）。 從表1可以看出，BPSO 獲得了數目最少的最優特征子集和最高的分類準確率。 在選出的特征集中，緊致度(F3)、平滑度(F5)、不規則度(F7)和灰度游程矩陣的長度不均勻性(F40)均被三種算法選中。 也就說，在甲狀腺結節超聲圖像中，結節形態的緊致度、邊緣的平滑度、形狀的不規則度于診斷具有重要價值。

表1 特征選擇方法的比較

3.2 分類器的比較 將BPSO 選出的最優特征子集（F3、F5、F7、F14、F23、F24、F40）依次用于訓練支持向量機（SVM）、貝葉斯分類器（Bayes）[17]和決策樹（DT）[18]分類器，均獲得了較好的分類效果。 其中，支持向量機仍獲得最高的分類準確率，決策樹因其推理的簡潔性在速度上具有優勢。 見表2。

表2 分類器的比較

3.3 甲狀腺結節良惡性風險評估計算機輔助診斷系統 將特征提取、選擇，分類器鑒別集成為計算機輔助診斷系統（圖2）。 影像醫生采集甲狀腺結節影像傳入系統，在線標記結節區域，系統提取上述77 個特征，使用分類器進行良惡性鑒別，最終輸出結果。在數據積累到迭代條件（每增加100 例患者）時，將重新施用BPSO 進行特征選擇，并生成新一代的最優特征集，迭代分類器，以不斷循環，提升分類性能。

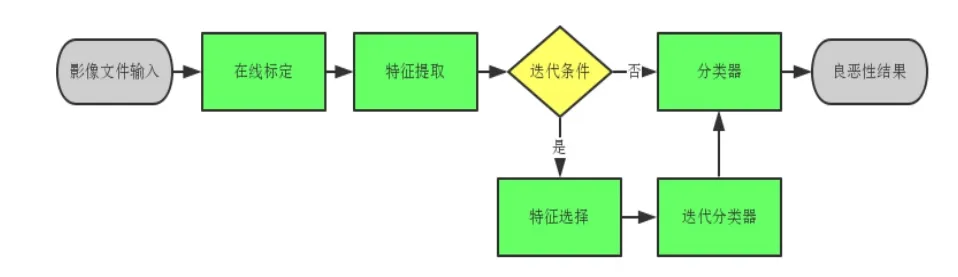
圖2 甲狀腺結節良惡性風險評估計算機輔助診斷系統流程圖

4 總結

臨床中，甲狀腺結節一般使用超聲檢查，結節圖像存在著豐富的形態和紋理等圖像特征。為了降低訓練成本，提高分類性能，幫助理解關鍵特征，可以使用特征選擇方法對原始特征集進行處理。本研究引入粒子群優化進行特征選擇，并施用于提取得到的77 個結節圖像特征， 用支持向量機訓練得到的分類器精度可達到98.20%， 性能超過了常規特征選擇方法得到的同類分類器。 研究結果表明，結節形態的緊致度、平滑度和不規則度在甲狀腺結節良惡性鑒別中起到關鍵作用。

[1] 中華醫學會內分泌學會 《中國甲狀腺疾病診治指南》 編寫組. 中國甲狀腺疾病診治指南——甲狀腺結節[J]. 中華內科雜 志, 2008, 47(10)：867-868. DOI： 10. 3321/j. issn： 0578-142 2008. 10.034.

[2] MR Carol, RW Stephanie, JW Charboneau, et al. Diagnostic ultrasound [M]. 3rd ed. Philadelphia： Elsevier Mosby,2005：735-757.

[3] Dash M, Liu H. Feature selection for classification[J]. Intelligent Data Analysis, 1997,1(4)： 131-156.

[4] Kennedy J, Eberhart R. Particle swarm optimization[C]// IEEE International Conference on Neural Networks [C]. Volume 4,1995(4)：1942-1948.

[5] Wouwer GV ,Scheunders P, Dyck DV. Statistical texture characterization from discrete wavelet representations[J]. IEEE Transactions on Image Processing, 1999, 8：592-598.

[6] Shapiro LG,Stockman GC.Computer Vision[M].[S.l.]：Prentice-Hall,Inc., Upper Saddle River, NJ, 2001.

[7] Galloway MM. Texture analysis using gray level run lengths[J].Computer Graphics And Image Processing, 1975, 4(2)：172-179.

[8] Pentland AP. Fractal-based description of natural scenes[J].Pattern Analysis and Machine Intelligence, IEEE Transactions on Medical Imaging, 1984(6)：661-674.

[9] Chu A, Sehgal CM, Greenleaf JF. Use of gray valu distribution of run lengths for texture analysis [J]. Pattern Recognition Letters, 1990, 11(6)：415-419.

[10] Chen CC, Chen CC. Filtering methods for texture discrimination [J]. Pattern Recognition Letters, 1999, 20 (8)：783-790.

[11] Zhou F, Feng JF, Shi Q. Texture feature based on local Fourier transform [C]//Image Processing, 2001. Proceedings. 2001 International Conference on. IEEE, 2001, 2：610-613.

[12] Schrijver A. Combinatorial optimization： polyhedra and efficiency[M]. [S.l.]：Springer, 2003.

[13] Kennedy J, Eberhart RC. A discrete binary version of the particle swarm algorithm[C]//Systems, Man, and Cybernetics,1997. Computational Cybernetics and Simulation, 1997 IEEE International Conference on. IEEE, 1997, 5：4104-4108.

[14] Kearns M, Ron D. Algorithmic stability and sanity-check bounds for leave-one-out cross-validation [J]. Neural Computation, 1999, 11(6)：1427-1453.

[15] Kira K, Rendell LA. The feature selection problem： traditional methods and a new algorithm[C]//AAAI, 1992： 129-134.

[16] Cortes C, Vapnik V. Support-vector networks [J]. Machine Learning, 1995, 20(3)：273-297.

[17] Zhang H. The optimality of naive Bayes[J]. AA, 2004, 1(2)： 3.

[18] Breiman L, Friedman J, Olshen R, et al. CART： classification and regression trees[M]. Wadsworth： Belmont, CA, 1983：156.