Riemann邊值在不同共形映射下的等價變換

江清華

（貴州師范大學(xué)數(shù)學(xué)與計算機(jī)科學(xué)學(xué)院，貴州 貴陽550001）

0 引言及主要結(jié)果

本文是研究解析函數(shù)邊值問題中的一種周期Riemann邊值問題，首先讀者應(yīng)該熟悉Plemelj公式及其廣義公式，它們是研究邊值問題的基本工具.為了文章的后續(xù)內(nèi)容的證明與陳述，讀者必須熟悉且掌握解析函數(shù)邊值問題研究中的一些基本符，相關(guān)定理，命題和定義。

1 Hold條件定義

1.1 設(shè)f(t)定義于（開口或封閉）光滑曲線L上，若對其上任意兩點(diǎn)t1，t2恒有α，(0＜α≤1)，A,α 都是確定的常數(shù), 則稱 f(t)在L上滿足α階的Hold條件或Hα條件,記為f(t)∈Hα(L)或簡記為f∈Hα,α稱為Hold指數(shù),也可以記為f(t)∈H(L)也可以這樣理解：,當(dāng)α=1時，條件H1也稱為Lipschitz條件.文章中討論的解析函數(shù)都是在H上進(jìn)行的.

1.3 設(shè)L是有限條互不相交的封閉曲線的集合，它把全平面分割成有限個區(qū)域。F(z)是這樣一個函數(shù)，它在每個這樣的區(qū)域中全純，在點(diǎn)z=∞處至多有一個極點(diǎn)，且當(dāng)z從L的任意確定的側(cè)趨于L上的任何點(diǎn)時，F(xiàn)(z)的極限值即邊值存在，則稱F(z)是以L為跳躍（或間斷）曲線的分區(qū)全純函數(shù)。如果L中含有開口弧段，則要求在各端點(diǎn)附近，F(xiàn)(z)有不到一階的奇異性，即若c為L的一端點(diǎn)，則在z=c附近，為常數(shù)。 在點(diǎn) z=∞ 處，F(xiàn)(z)的 Laurent展式為：F(z)=,則稱F(z)在點(diǎn)z=∞處為k階的或階數(shù)為 k。當(dāng) k＞0時，它以z=∞為k階極點(diǎn)；當(dāng)k＜0時，它以 z=∞為-k階零點(diǎn)；k=0時，表示F(∞)≠0且有限。因此分區(qū)全純函數(shù)F(z)要求在z=∞處有有限階。

1.4 設(shè)z從封閉曲線L的正向（逆時針旋轉(zhuǎn)方向）的左側(cè)趨于L上某點(diǎn)t時（不包括開口弧段的端點(diǎn)）F(z)的邊值存在記為F+(t)，而當(dāng)z從L的負(fù)向（順時針旋轉(zhuǎn)方向）趨于t時，邊值記為F-(t)；而把φ(t)=F+(t)-F-(t)稱為F(z)在t處的跳躍或躍度，φ(t)關(guān)于t的函數(shù)，稱為跳躍函數(shù)。

1.5 在Riemann邊值問題中涉及到解的一般形式，設(shè)，其中Pm(z)為任意m次多項式，即在這個解中含有m+1個任意復(fù)常數(shù)，我們稱它是有m+1個復(fù)的自由度。(見[3])

1.6 一個分區(qū)全純函數(shù) X(z)滿足以下三個性質(zhì)：（1）X+(t)=G(t)X-(t)；（2）在整個有限復(fù)平面上 X(z)≠0，包括在L上X±(t)≠0；（3）在點(diǎn) z=∞ 處 X(z)有有限階，則稱X(z)為一個Φ+(t)=G(t)Φ-(t)，t∈L的一個典則函數(shù)。

1.7 設(shè)L是一條逐段光滑的曲線，f(t)∈H于L上，則對于任何t0∈L(當(dāng)L為開口曲線時，t0不為端點(diǎn))，Cauchy型積分的邊值存在，且有下列 Plemelj公式：；其中 F+(t0),F+(t0)表示 F(z)當(dāng) z 分別從 L 的正側(cè)和負(fù)側(cè)趨于t0時的極限值，而θ0是L在t0處的兩單側(cè)切線在L正側(cè)所張的角(0≤θ0≤2π).特別注意，當(dāng)t0是L上的光滑點(diǎn)時，或者整個L是光滑曲線，則上述兩等式可合寫成為：

2 定理

2.1 定理1

如果 Φ(±∞i)有界，則齊次的周期 Riemann邊值問題：Φ+(t)=G(t)Φ-(t)+g(t)，g(t)≡0。當(dāng)指標(biāo) κ≥0 時有 κ+1 個線性無關(guān)的解；當(dāng) κ＜0 時只有零解。

2.2 定理2

如果Φ(±∞i)有界，則非齊次的周期Riemann邊值問題：Φ+(t)=G(t)Φ-(t)+g(t)，t∈L。 當(dāng) κ≥-1時，其一般解中含有 κ+1個任意常數(shù)；當(dāng) κ＜-1時，當(dāng)且僅當(dāng)滿足-κ-1個條件有唯一解，解的自由度為κ+1。

3 主要結(jié)果的證明

3.1 準(zhǔn)備工作

在涉及到解析函數(shù)邊值問題時，通常會遇到所謂的Riemann周期問題，在此簡記為PR 問題。 設(shè) Li（i=0,±1,±2,…）為無窮條封閉光滑曲線，它們彼此形狀相同，互不相交，且以kπ（k＞0）為周期水平地排列，Li均以逆時針方向為正方向。記的內(nèi)部記為，外部記為。不妨設(shè)原點(diǎn),而；這樣可以辦得到的。周期Riemann邊值問題為：求一個以kπ為周期的分區(qū)全純函數(shù)Φ(z)，以L為跳躍曲線（此時 z=∞ 不能為極點(diǎn)），使得 Φ+(t)=G(t)Φ-(t)+g(t)，t∈L，其中 G(t)，g(t)在 L 上都屬于 H，且 G(t)≠0，它們都是以 kπ 為周期的：G(t)=G(t+kπ)，g(t)=g(t+kπ)，當(dāng)時 g(t)≡0 稱為齊次的；否則，稱非齊次的。[3]z=∞點(diǎn)是各曲線Li之并所成點(diǎn)集的聚點(diǎn)，在z=∞處一般無極限，當(dāng) z=±∞i是指 z=x+yi，x為任意的值，y→±∞，此時可以對 Φ(z)賦予一定的條件就可以滿足需求。在問題當(dāng)中，我們只要求Φ(z)也是以kπ為周期，在適當(dāng)?shù)沫h(huán)境下可以做的，因為對于齊次而言，若Φ1(z)是它的一個非零周期解，但是對于非周期整函數(shù)I(z)來說，Φ(z)I(z)也是它的解，但不是具有周期性的解。首先我們作一個共形映射把問題：轉(zhuǎn)化為普通的Riemann邊值問題，作帶形區(qū)域S0：，設(shè)L0位于S0之中，并在直線上取定正方向，使位于其右側(cè)，若Φ(z)為PR問題的解，其在S0中部分記為Φ0(z)是S0中的分區(qū)全純函數(shù)，可以連續(xù)至兩直線：上，以L0為跳躍曲線，且滿足下列兩等式：反之，若Φ0(z)在S0中分區(qū)全純且連續(xù)至兩直線：

3.2 定理1的證明

在此篇文章中，限制 Φ(±∞i)有界，亦即 Φ*(ζ)在 ζ=0,∞ 處有界，從而正則，根據(jù)通常的Riemann邊值問題的結(jié)果（現(xiàn)在是在R0中求解），這時此式：的解為：，其中，當(dāng)指的是 Γ0內(nèi)域)時，；當(dāng)指的是 Γ0的外域） 時，， 在這里的，而且 Pκ(ζ)為 κ 次任意多項式（當(dāng) κ＜0 時，記。現(xiàn)在再回過頭來考慮z平面則有：，其中，（1）當(dāng)時，；

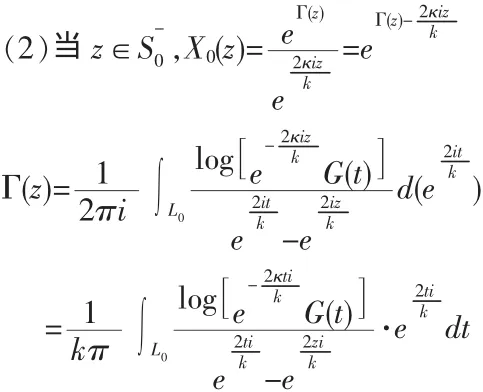
把常系數(shù)eC并入到多項式中，因此可以認(rèn)為：。其中對數(shù)可以任取定一支，將Φ0(z)作周期延拓，則周期Riemann邊值問題的一般解形式為仍稱為PR問題的典則函數(shù)，(見[4])上述一般解也可以用另外一種形式替代，是用到分區(qū)全純函數(shù)的概念進(jìn)行表達(dá)的：當(dāng)；當(dāng) z∈S-時，，其中是關(guān)于以為變量的 κ 次任意多項式（κ＜0,Qκ≡0），證畢。

3.3 定理2的證明

［1］杜金元.廣義∏PHBaπOB定理及Plemelj公式的簡單證明[R].數(shù)學(xué)研究報告(武漢大學(xué)),1980,5：43-50.

［2］L.V.Ahlfors.復(fù)分析[M].趙志勇,薛運(yùn)華,楊旭,譯.機(jī)械工業(yè)出版社,2005,7.

［3］路見可.解析函數(shù)邊值問題[M].武漢大學(xué)出版,2004,10.

［4］聞國椿.共形映射與邊值問題[M].北京：高等教育出版社,1985,10.

［5］鐘玉泉.復(fù)變函數(shù)論[M].高等教育出版社,2003,6.

［6］章紅梅,王傳榮.Riemann邊值問題的解關(guān)于邊界曲線的穩(wěn)定性[J].福州大學(xué)學(xué)報,2001,29：1-4.