季節性指數平滑法預測深圳市寶安區涂陽肺結核發病人數的應用

張 磊 劉艷紅

廣東省深圳市寶安區慢性病防治院，廣東深圳518133

季節性指數平滑法預測深圳市寶安區涂陽肺結核發病人數的應用

張 磊 劉艷紅

廣東省深圳市寶安區慢性病防治院，廣東深圳518133

目的應用季節性指數平滑法對深圳市寶安區2015、2016年的涂陽肺結核病人數進行預測。方法收集2005～2014年深圳市寶安區每月確診的涂陽結核人數，通過SPSS 20.0統計學軟件進行指數平滑法預測，經過簡單季節性模型、Winters加法模型和Winters乘法模型的指標分析、統計量分析、殘差圖分析對三種模型進行了全面評估，同時給出了2015、2016年的結核病發病估計人數。結果簡單季節性模型、Winters加法模型和Winters乘法模型的R2分別為0.69、0.69、0.67，Ljung-Box的概率為0.86、0.79、0.67，Alpha值為0.40、0.40、0.32，均顯示模型擬合良好，可以做出良好的預測結果。結論涂陽肺結核結核病在深圳市寶安區進入下降通道，但幅度緩慢，應進一步加強結核病的防治工作。

指數平滑法；結核病；預測；寶安區

結核病是一種嚴重危害人民群眾健康的呼吸道傳染病，在國家法定乙類傳染病發病率排名靠前，因此需要進一步加大對結核病防控領域的研究。利用歷史資料判斷結核病的趨勢、科學評價現有防控措施的效果對結核病防控意義重大。指數平滑法作為一種時間序列分析的預測方法，可以進行中短期預測。本文采用指數平滑法研究深圳市寶安區涂陽結核患者2005～2014年的月份資料，擬合結果較為理想。現將方法與結果報道如下：

1 資料與方法

1.1 一般資料

涂陽結核病資料來源于深圳市寶安區慢性病防治院（以下簡稱“我院”），寶安區結核病實行歸口管治，全區的結核病均在我院確診和治療，數據為深圳市寶安區2005年1月～2014年12月涂陽肺結核病發病人數。

1.2 方法

由于本資料有季節性變化，因此采用指數平滑法中的簡單季節性模型、Winters加法模型和Winters乘法模型對寶安區2005年1月～2014年12月的數據建立模型，并對各個模型進行數量化評價，最后預測2015、2016年各個月份的涂陽患者數。

1.3 統計學方法

采用SPSS 20.0統計學軟件進行數據分析，按照年月的格式對數據定義，將數據轉換為時間序列，利用時間序列模型中的3種指數平滑法分別建立模型，分析擬合指標，繪制殘差圖，并利用模型預測2015、2016年各個月份的涂陽肺結核發病人數。

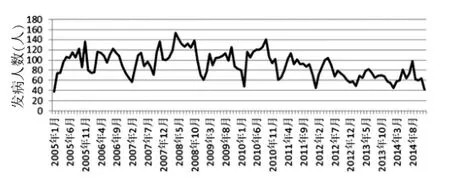
圖1 2005～2014年深圳市寶安區每月涂陽發病人數

2 結果

2.1 2005～2014年的數據描述

對2005～2014年各個月份的發病人數進行整理，發現每年的發病人數呈緩慢下降趨勢，同時每年的數據存在周期性波動，符合季節性指數平滑法的要求。見圖1。

2.2 指數平滑法的擬合結果分析

各個模型均給出了多個擬合優度指標，其中3個模型平穩R2為0.69、0.69、0.67，表明這3個模型均優于簡單均值模型（簡單均值模型，moving-average，即MA模型，模型參量法分析方法之一，也是時間序列分析方法中常用的模型，MA模型參數估計常作為ARMA參數譜估計的過程來計算），簡單季節性和Winters加法模型R2均為0.69，略高于Winters乘法模型的0.67，說明總變異中模型可以解釋的部分將近70%；各個模型的Ljung-Box的概率為0.86、0.79、0.67，說明殘差序列是沒有自相關性的，而各個模型的殘差圖均表明殘差屬于隨機誤差，因此采用指數平滑法較為合適。見表1、圖2～4。

表1 各模型的擬合指標分析

2.3 各個模型的統計量分析

3種模型的參數均表明本次研究的時間序列僅在Alpha（水平）上差異有統計學意義（P＜0.05），值在0.3～0.4，而在Delta（季節）和Gamma（趨勢）差異無統計學意義（P＞0.05），說明本次的時間序列并沒有季節趨勢和線性趨勢。見表2。

2.4 預測結果

各個模型給出了2015、2016年間每個月寶安區涂陽肺結核發病人數的預測值，具體見表3、4。

3 討論

美國經濟學家布朗于1959年首先提出了指數平滑法的概念，他認為時間序列的態勢具有穩定性或規則性，以時間序列可被合理地順勢推延；認為最近的過去態勢在某種程度上會持續到未來。指數平滑法作為時間序列分析的一種重要方法［1-3］，具有方法簡潔、使用范圍廣、充分利用歷史資料信息等優點，可以對不規則的時間序列數據加以平滑［4］，它統一考慮了所有已有時間序列資料對預測值的影響［5］，以此對未來數據進行推斷和預測等優勢［6］，因而在很多領域中發揮著越來越重要的作用［7-13］，適用于中短期預測［14］。

由于本次的數據均為月份數據，因此采用了指數平滑法的3種季節性模型：簡單季節性模型、W inters加法模型和Winters乘法模型，分別適用于序列具有線性時間趨勢但無季節性變化、具有線性趨勢和加法季節變化以及具有線性趨勢和乘法季節變化［15］。指數平滑法是一種特殊的加權移動平均法，加強了近期觀測值對預測值的作用，由近至遠的權數之間按等比級數遞減，等比級數首項是平滑系數Alpha［16］。平滑系數取值的大小決定了權數變化的快慢，數據如果波動較大則取值0.3～0.5。本次3種方法的Alpha均在這個波動范圍。簡單季節性模型中主要包括Alpha（水平）和Delta（季節）兩個指標，Winters加法和Winters乘法有Alpha（水平）、Gamma（趨勢）和Delta（季節）3個指標，其中，3個模型均認為只有Alpha（水平）指標有統計學意義。從各個模型的擬合結果分析表來看，絕大多數指標都非常接近，R2表示模型所能解釋的數據變異占總變異的比例，該數據越大表示結果越佳，3個指標的R2分別為0.68、0.68和0.64，顯示模型擬合較好。Ljung-Box Q是檢驗殘差序列是否為獨立序列的假設檢驗，當假設檢驗的P值＞0.05時，說明數據擬合后的殘差序列是不存在自相關的，可以采用指數平滑序列模型。另外，各個指標的殘差圖也說明了這一點。

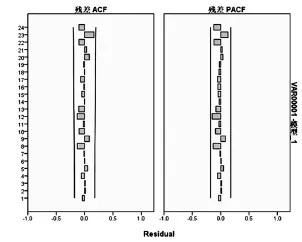
圖2 簡單季節性模型殘差圖

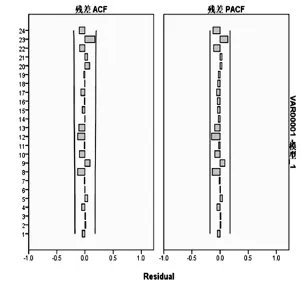
圖3 W inters加法殘差圖

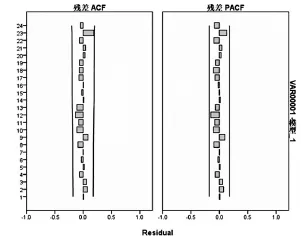
圖4 W inters乘法殘差圖

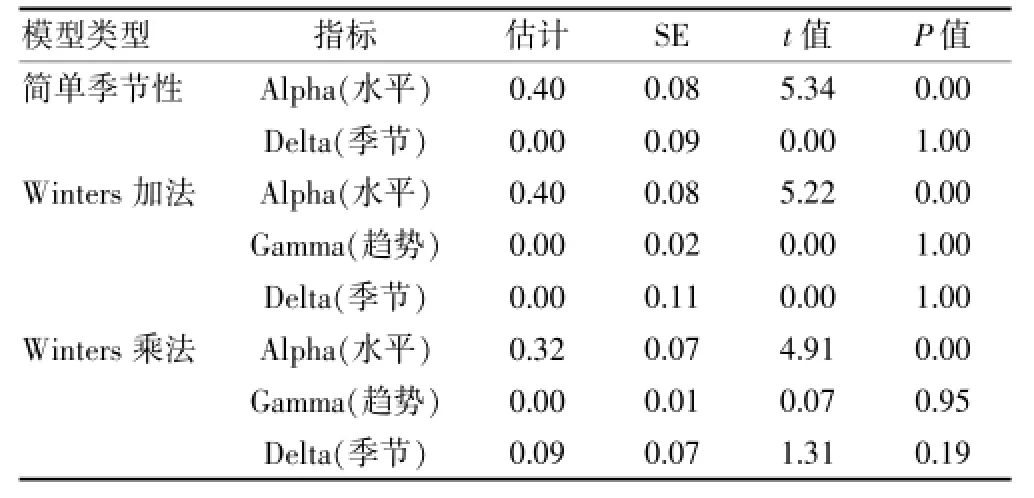
表2 各個模型統計量分析

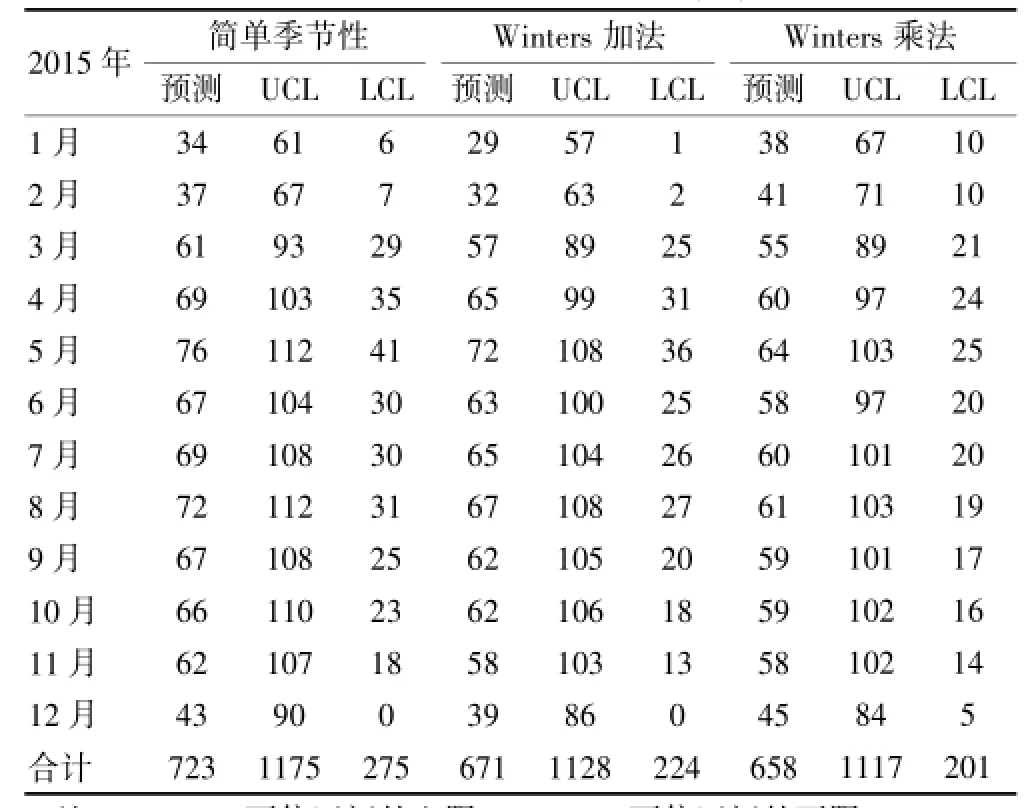
表3 各模型對2015年各月份寶安區涂陽肺結核發病人數的預測（例）

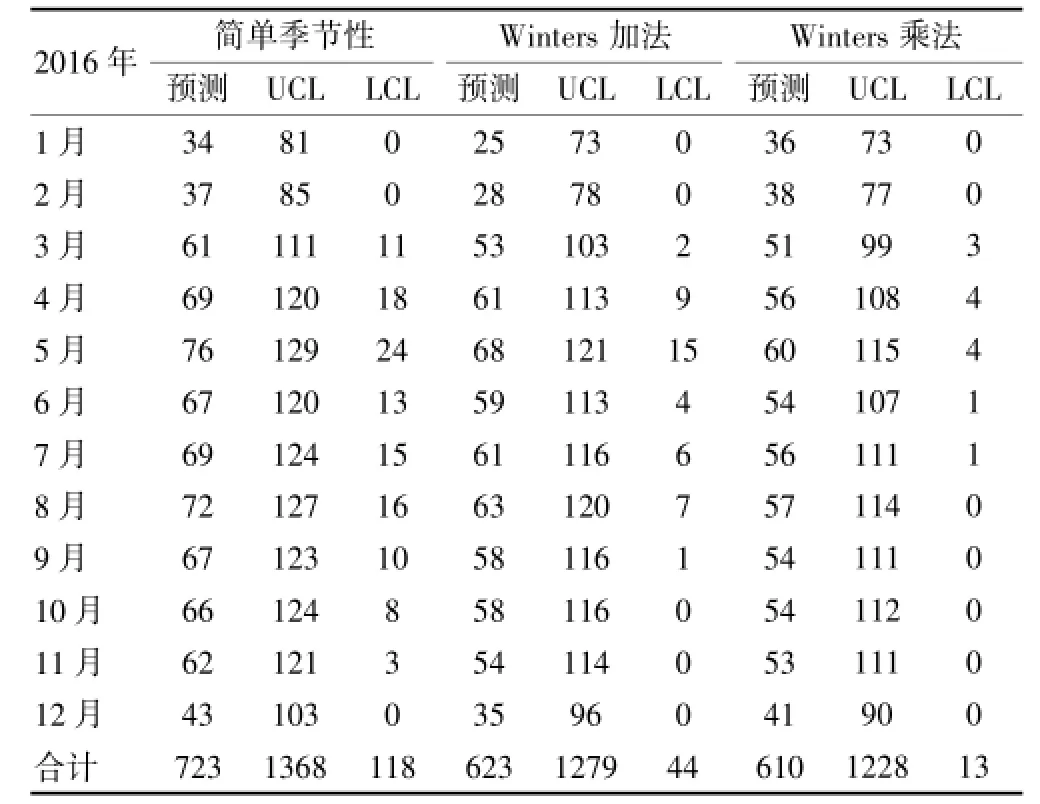
表4 各模型對2016年各月份寶安區涂陽肺結核發病人數的預測（例）

模型的最終意義在于預測結果，3種模型均給出了未來2年的預測結果及95%的可信區間（95%CI），3種模型均提示寶安區涂陽肺結核發病人數每月的數據與往年同期比較，均有小幅的下降。寶安區是深圳的一個人口大區，結核病的預防控制一直受到寶安區政府、衛生行政部門的廣泛關注和支持。在政府的支持下，寶安區在結核病的預防控制方面做了許多工作。1987年正式成立了寶安區慢性病防治院，負責全區的結核病防治工作。1993年成立了寶安區世界銀行貸款中國結核病控制項目領導小組。進入“十一五”以來，為了進一步加強結核病控制工作，寶安區政府把結核病列為重點控制的重大傳染病之一，將結核病控制納入地區經濟社會發展總體規劃，采取了一系列重大舉措，遏制結核病傳播，并取得了一定的成就。制訂了區域結核病防治規劃，提出了新發涂陽病人發現率、治愈率等工作指標，將外來人口納入結核病控制規劃。區財政把結核病防治經費納入地方財政預算，每年為控制結核病下撥專項經費，下撥額度逐年上升。在政府、衛生行政部門的領導下，寶安區已建立“政府領導、各部門協作和全社會參與”的預防與控制結核病可持續發展的有效機制。區政府履行承諾，不斷加大對結核病防治工作的領導和專項資金的投入，進一步增強做好結核病控制工作的緊迫感和責任感，確保結核病控制工作的順利實施。

本次利用深圳市寶安區2005～2014年的數據進行指數平滑法預測，通過3種模型的分析比較，認為寶安區已經基本遏制了結核病的上升勢頭，未來結核病發病人數處于下降通道，說明結核病控制策略恰當，防治效果明顯。但同時也清楚的看到，雖然有下降的趨勢，但是下降緩慢，需要進一步加大對結核病的防控力度，從而控制結核病的流行。

［1］朱奕奕，趙琦，馮瑋.應用指數平滑法預測上海市甲型病毒性肝炎發病趨勢［J］.中國衛生統計，2013，30（1）：31-33，36

［2］李建華，周挺進.基于指數平滑法的環境噪聲污染預測模型及應用［J］.環境科學與管理，2012，37（7）：50-53.

［3］González Díaz A，Sánchez Valdés L，Armas Pérez L，et al. Trends and predictions of tuberculosis，and challenges towards tuberculosis eradication in Havana City［J］.Rev Cubana Med Trop，2012，64（2）：163-175.

［4］Rimaityte I，Ruzgas T，Denafas G，et al.Application and evaluation of forecastingmethods formunicipal solid waste generation in an Eastern-European city［J］.Waste Manag Res，2012，30（1）：89-98

［5］吳健華，李培月，錢會.基于Holt指數平滑模型的地下水水質預測［J］.工程勘察，2013，10：38-41，48

［6］劉震，吳廣，丁維貸，等.SPSS統計分析與應用［M］.北京：電子工業出版社，2011：344.

［7］周炳飛.動態指數平滑模型預測及應用［J］.哈爾濱師范大學自然科學學報，2013，29（4）：5-27.

［8］王昕，程小雯，房師松，等.指數平滑模型在流感樣病例預測中的應用［J］.中國熱帶醫學，2011，11（8）：938-939.

［9］張磊，劉艷紅.指數平滑法在預測深圳市寶安區肺結核病人發病人數的應用［J］.實用預防醫學，2014，21（8）：930-933.

［10］顏惠琴，韓惠麗.基于指數平滑法的寧夏沿黃經濟區煤炭資源需求的數學模型［J］.區域經濟，2014，（2）：44-45，48.

［11］鄧文，楊玉.2011年-2015年湖南省糧食供需狀況狀況預測［J］.湖南農業科學，2013，（9）：127-130.

［12］張澍，于霞.基于指數平滑法預測企業貨運量［J］.林業機械與木工設備，2014，42（1）：55-57.

［13］張文勛.基于灰色預測法和指數平滑法預測研究新疆安全生產事故［J］.安全，2013，（11）：28-30.

［14］關國瓊，向德尚，胡傳慧.我院出院人數預測模型分析［J］.中國衛生統計，2011，28（6）：712-713.

［15］劉珍文.指數平滑技術在出院人數預測中的應用研究［J］.中國衛生統計，2011，28（4）：459，461.

［16］榮潔，王臘春.指數平滑法——馬爾科夫模型在巢湖水質預測中的應用［J］.水資源與水工程學報，2013，24（4）：98-102.

Prediction of the onset number of smear positive pulmonary tuberculosis in Bao'an District of Shenzhen City w ith seasonal exponential smoothing method

ZHANG Lei LIU Yanhong
Bao'an Chronic Disease Prevention and Control Hospital of Shenzhen City,Guangdong Province,Shenzhen 518133, China

Objective To predict the onset number of smear positive pulmonary tuberculosis in Bao'an District of Shenzhen City in the year 2015 and 2016 with seasonal exponential smoothingmethod.M ethods Themonthly number of smear positive tuberculosis from 2005 to 2014 in Bao'an District of Shenzhen City was collected to predict the resultswith exponential smoothingmethod by SPSS 20.0.Three kinds ofmodels were overall evaluated after index analysis,statistic analysis,residual plot analysis of simple seasonalmodel,Winters addition model and Wintersmultiplication model,and the onset number of smear positive pulmonary tuberculosis in the year 2015 and 2016 was estimated. Results The R2of simple seasonalmodel,Winters addition model and Wintersmultiplicationmodel was 0.69,0.69 and 0.67 respectively;P value of Ljung-Box was 0.86,0.79 and 0.67;Alpha value was 0.40,0.40 and 0.32 respectively. Themodel fitting and predictions was good.Conclusion The estimated onset number of smear positive pulmonary tuberculosis will be decreased in Bao'an District of Shenzhen city,but the rate is slow,tuberculosis prevention should be further strengthened.

Exponential smoothingmethod;Tuberculosis;Prediction;Bao'an District

R521

A[文獻標識碼]1673-7210（2015）06（c）-0039-04

2015-03-16本文編輯：程銘）

廣東省深圳市科技計劃項目（201203266）。

張磊（1981.2-），男，中南大學2011級流行病與衛生統計學專業在讀博士研究生；研究方向：傳染性疾病控制。