柱式墩順橋向計算長度影響因素分析

李群鋒

（山西省交通科學研究院，山西 太原 030006）

由于預制裝配式柱式墩連續梁橋施工方便、造價經濟，因而在高速公路橋梁工程中得到了廣泛的應用。該種橋型在設計過程中，重點是要優化下部結構設計，盡量做到結構尺寸合理，受力均勻，經濟節約。目前在橋墩計算長度系數取值上，往往直接采用經驗值[1]。然而通過一些分析軟件（如Midas）精確分析后，我們會發現：在多跨一聯橋梁中，經常出現矮柱計算長度系數取值偏小，而高柱（超過30 m）取值可能偏大的情況，這樣在理論上就造成高柱配筋設計偏于保守，而矮柱則會出現配筋不足。好在我們在實際設計過程中，往往以一聯受力最不利的柱子作為參考配筋。即便如此，精確分析一聯各個柱子的計算長度系數對實際工程設計仍有指導意義。

1 墩柱計算長度理論推導公式

對于連續梁橋的柱式墩，如不考慮軸力偏心，可以將其看做理想彈性支撐軸心受壓桿。大多數實際結構中，壓桿的端部既不是鉸接也不是固定[2]。而對于橋梁結構中柱式墩，則可以將其模擬成下端固定（假想固結點處），上端彈性約束支撐的軸心壓桿模型。通過建立該模型的屈曲平衡微分方程，可得穩定方程[3]：

式中：l為墩頂到假想固結點的高度；h為墩柱高（含蓋梁）；d為沖刷深度；D為樁徑；α為樁的變形系數，見規范JTG D63—2007附錄P.0.2[4]；EhI0為墩柱混凝土彈性模量與樁柱換算慣性矩的乘積；K為墩柱頂約束剛度。

通過求解超越方程（1）中的α0值，得出構件計算長度l0=π/α0。

2 工程概況及Midas分析模型

本橋為五跨一聯先簡支后連續雙柱式連續梁橋，橋寬B=12 m，跨徑組合為L=5×30 m，墩柱、樁基直徑分別為1.6 m、1.8 m，蓋梁高度1.6 m。橋墩板式支座總抗推剛度K=16755 kN/m，橋臺為滑板支座。墩柱、樁基混凝土等級分別為C35、C30，本橋不考慮水流沖刷，即d=0。各墩柱高、樁長詳見圖1。

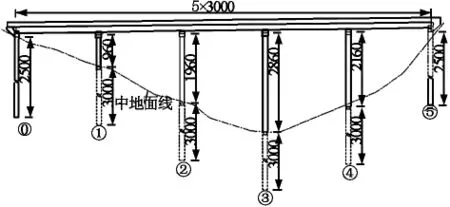
圖1 橋型立面示意圖（單位：cm）

對該聯橋梁主要分析1～4號墩柱的計算長度，為了與墩柱計算長度理論推導公式進行對比分析，采用Midas有限元分析軟件分別建立了1～4號墩柱的屈曲分析模型，模型中考慮了墩頂約束剛度K以及樁-土的相互作用，具體模型示意圖見圖2。

圖21～4號墩柱屈曲分析模型

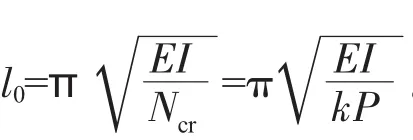
3 地基土比例系數m對墩柱計算長度系數的影響規律

本文針對文獻[4]附錄P.0.2中的六類非巖石類土的m取值區間，擬定m=3000 kN/m4、m=5000 kN/m4、m=10000 kN/m4、m=20000 kN/m4、m=30000 kN/m4、m=80000 kN/m4、m=120000 kN/m4共7種情形。對五跨一聯連續梁橋1～4號墩柱的計算長度系數進行對比分析。本文墩柱計算長度系數，則通過理論推導公式和Midas有限元分析軟件兩種分析方法得出。墩頂約束剛度K值計算方法詳見文獻[3]。1～4號墩柱計算長度系數值對比分析結果如圖3～4所示。

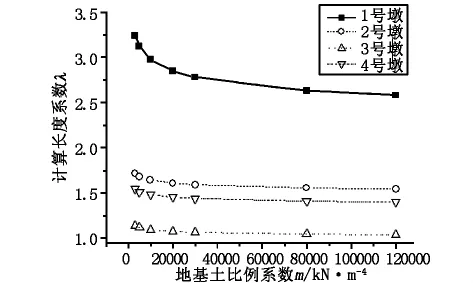
圖31～4號墩計算長度系數λ值（理論公式）

從圖3～圖4中可以看出：a）隨著地基土比例系數m的逐漸增大，1～4號墩柱計算長度系數λ均在不斷減小。b）地基土比例系數m對矮墩的計算長度系數影響較大，而對高墩則影響較小。c）從曲線圖中可以看出，計算長度系數λ與地基土比例系數m之間為非線性關系，λ值減小斜率逐漸變小。d）隨著地基土比例系數m趨于無窮大時，墩柱計算長度系數也無限趨近于某個常值，而該常值就是墩底理想固結狀態下墩柱的計算長度系數。為此，本文也給出了墩底理想固結情形下1～4號墩柱的計算長度系數λ值，詳見表1。

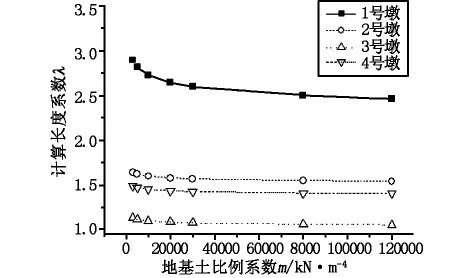
圖4 1～4號墩計算長度系數λ值（Midas）

表1 墩底固結情形下1～4號墩柱的計算長度系數λ值

4 不同墩柱高對墩柱計算長度系數的影響規律

對于一聯多跨的連續梁橋，不同墩柱高的墩柱計算長度系數也不相同，本文就1～4號4種不同墩柱高的墩柱計算長度系數λ值在各種地基土比例系數m值下的分布規律進行探討。圖5～圖6分別為理論公式和Midas分析結果。

圖5 墩柱計算長度系數分布圖（理論公式）

圖6 墩柱計算長度系數分布圖（Midas）

從圖5～圖6中可以看出：在各種地基土比例系數m值下，1號墩墩柱高最小，其墩柱計算長度系數λ值也最大，其次為2號墩和4號墩，3號墩墩柱高最大，其墩柱計算長度系數λ值也最小。由此說明，在多跨一聯連續橋梁中，墩柱高越大，計算長度系數越小；墩柱高越小，計算長度系數越大。

5 分聯設計對墩柱計算長度系數的影響規律

本文全橋為五跨一聯連續梁橋，該小節擬定地基土比例系數m=10000 kN/m4不變，通過改變全橋分聯方式來研究分聯設計的變化對墩柱計算長度系數的影響規律。全橋共5孔，分聯設計情況如下：五孔一聯為1～5孔；四孔一聯方案有：方案1為1～4孔，方案2為2～5孔；三孔一聯方案有：方案1為1～3孔，方案 2為 2～4孔，方案 3為 3～5孔；兩孔一聯方案為各個橋墩的相鄰兩孔。通過理論計算和Midas軟件對比分析，得出各種分聯設計狀態下的墩柱計算長度系數λ值分別見表2、表3。a）隨著一聯孔數的減小，1～4號墩柱計算長度系數λ值在不斷增大，并且呈現墩身越低，λ值增大幅度越小，墩身越高，λ值增大幅度越大的規律。b）當一聯孔數相等時，不同的分跨設計方式也影響各個墩柱的計算長度系數。比如四孔一聯的情形，方案1的2號、3號墩柱計算長度系數就比方案2要小。

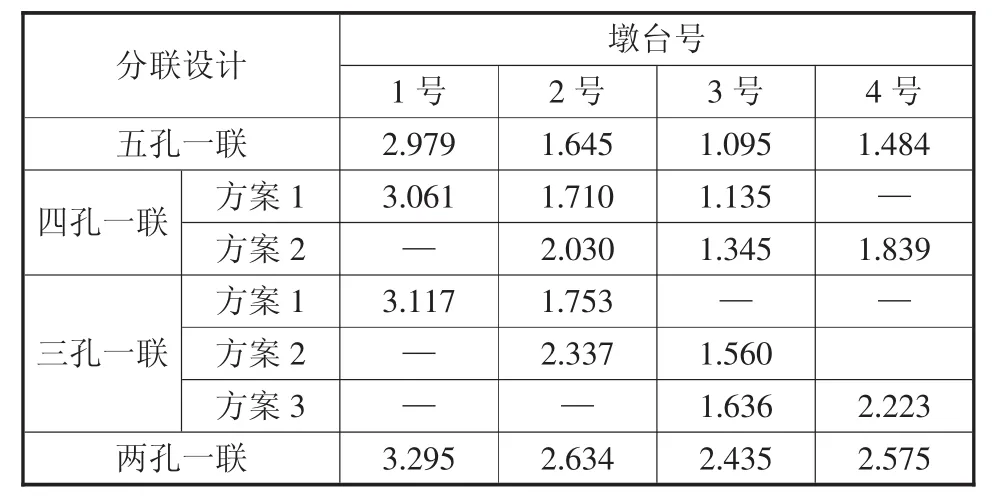
表2 各個分聯設計狀態下墩柱計算長度系數（理論公式）

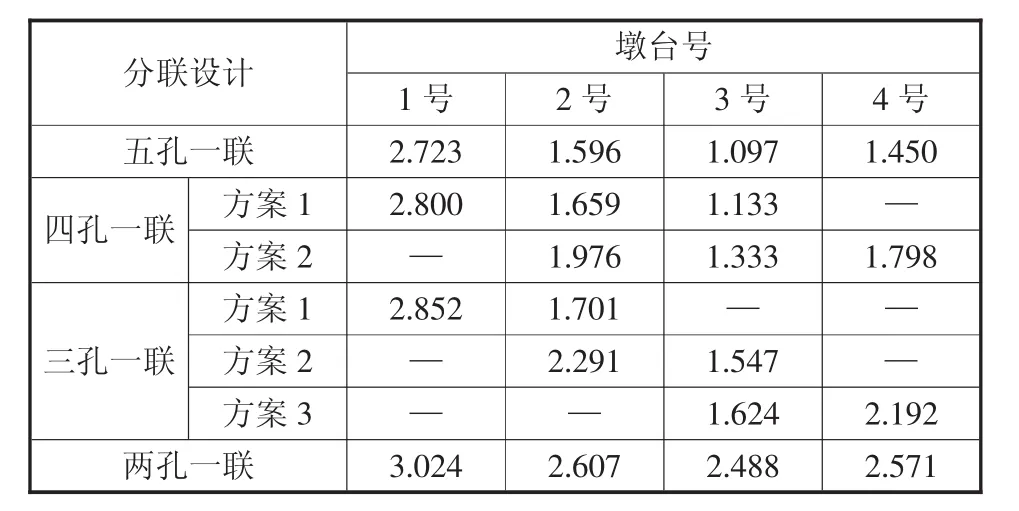
表3 各個分聯設計狀態下墩柱計算長度系數（Midas）

6 結論

a）對于一聯多跨柱式墩連續橋梁，墩柱計算長度系數λ值隨地基土比例系數m的增大而減小，且兩者之間呈現非線性關系。同時，地基土比例系數m對矮墩的計算長度影響較大，而對高墩則影響很小。

b）在多跨一聯連續橋梁中，高墩的計算長度系數小，矮墩的計算長度系數大。

c）在多跨橋梁分聯設計中，一聯孔數越少，該聯各墩柱計算長度系數越大，而且一聯孔數的變化對矮墩計算長度系數影響較小，而對高墩則影響較大。此外，當一聯孔數一定時，不同的分聯方式也會影響到墩柱的計算長度系數。因此，對于多跨連續橋梁設計伊始就應該結合墩柱計算長度這一因素合理地進行分聯設計，以便盡量減小各墩柱計算長度系數，以利于后期的墩柱配筋設計。