駐波型直線超聲波電動機分析與測試

蔣春容，張津楊，陸旦宏，張小蓮

(南京工程學院，南京211167)

0 引 言

超聲波電動機結構設計靈活，利用不同的壓電陶瓷極化形式和彈性體的振動模態，可以構造出不同結構的超聲波電動機［1－5］，直線超聲波電動機是其中的一種。從結構上看，直線超聲波電動機也有多種不同的類型。Wang Hong－xiang 等［6］提出了一種梁式結構的直線超聲波電動機，該電機的上下兩個直梁分別粘貼有兩組壓電陶瓷，通過施加一定頻率的電壓激勵出定子的駐波運動，兩個動子通過一定的預壓力分別與兩側的定子齒接觸。Huang Weiqing 等［7］提出了一種直線超聲波電動機，電機的定子由兩個縱向振動的作動器組成，兩個作動器頂端通過一個半圓形結構連接在一起，驅動足放置在半圓結構的外側，驅動與之接觸的滑塊作直線運動。直線超聲波電動機作為超聲波電動機的重要分支，除具有超聲波電動機的低速大力矩、動態響應快、不受電磁場影響等優點外，還具有無需絲桿機構運動轉換直接輸出直線運動、結構簡單等優點［8］，作為控制系統執行元件在微機電系統中應用前景廣闊［9］。

本文研究一種駐波型直線超聲波電動機，首先分析其結構和工作原理，進而用解析法建立電機金屬彈性體的振動模型，分析其自由振動的模態和頻率，并與有限元法分析結果進行比較，接著對樣機進行了阻抗－頻率特性測試以驗證理論分析結果，最后設計了一種電接觸測試法，對電機的驅動足與地面的接觸狀態進行了研究。

1 電機的結構與工作原理

所研究的駐波型直線超聲波電動機的結構如圖1 所示。電機的振動體可視為一個矩形等截面金屬梁，梁的上表面黏結有一片壓電陶瓷，下表面有兩個驅動足，整個電機為一個動子，電機工作模態為橫向一階彎曲振動模態，振動時為自由－自由邊界條件。對于自由－自由的梁，在以橫向一階彎曲振動模態工作時，梁上的兩個節點A、B 的橫向位移為零。將驅動足1 設置在節點A 的左邊，驅動足2 設置在節點B 的左邊，但不超過梁的中點。當在壓電陶瓷上施加激勵電壓時，設電機首先中間向上拱起，則驅動足1 受到向右下方的推力，與地面接觸，驅動足2 受到向左上方的拉力，與地面逐漸脫離，驅動足1 底部摩擦力大于驅動足2 的摩擦力，則電機向左移動一步;接下來電機中間下凹兩端上翹，驅動足1 受到向左上方的拉力，逐漸與地面脫離，驅動足2 受到向右下方的推力，與地面接觸，電機繼續向左移動一步。通過適當選擇兩個驅動足的位置，可以使電機工作在橫向一階彎曲振動模態時往左行進，工作在橫向二階彎曲振動模態時往右行進，從而通過改變驅動電壓的頻率而改變電機的運行方向，實現電機的雙向運行。

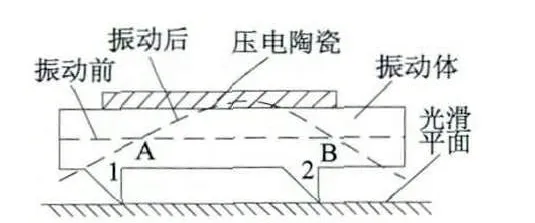
圖1 駐波型直線超聲波電動機的結構

2 電機的振動分析

采用解析法對電機振動體進行振動分析，以確定電機的振動模態和對應的頻率。對于矩形等截面梁，橫向彎曲自由振動的方程［10］:

式中:w(x，t)為梁橫向振動的位移;E，I，ρ 和A 分別為彈性模量、截面慣性矩、密度和截面積。式(1)的解可用變量分離法得到:

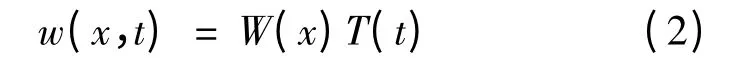
將式(2)代入式(1)整理可得:

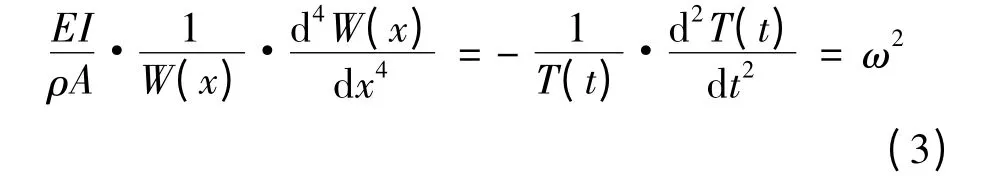
式中:ω 為角頻率。式(3)可寫為兩個方程:

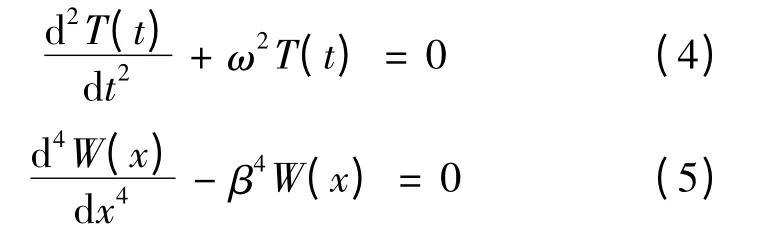
式中:

滿足式(4)的解:

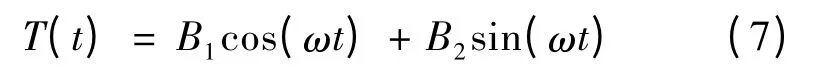
常數B1和B2由初始條件決定。式(5)的解可寫:

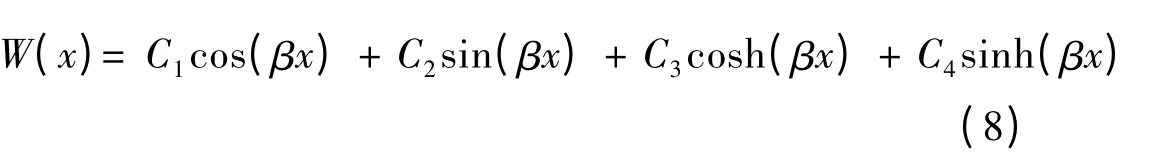
式中:C1，C2，C3和C4均為常數，由邊界條件決定。電機振動體可視為自由－自由梁，其邊界條件:

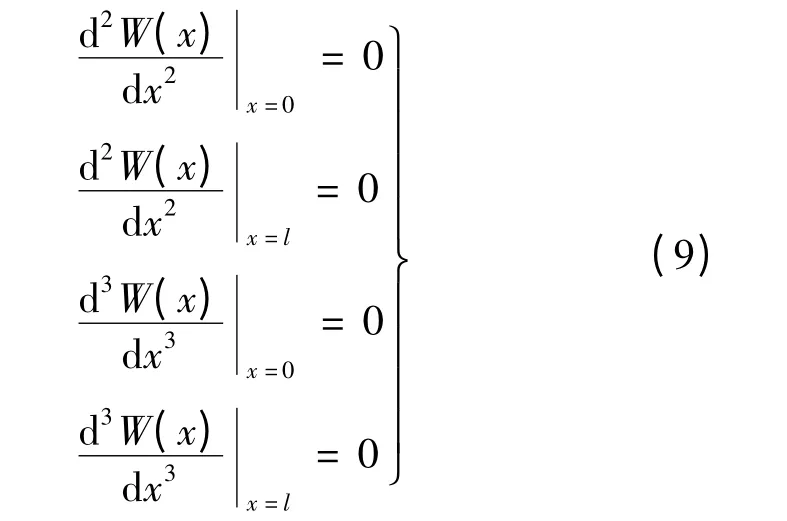
式中:l 為梁的長度。根據以上邊界條件有:

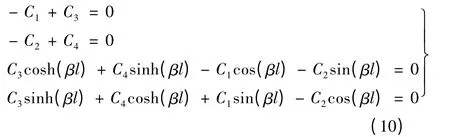
式(10)又可簡化:

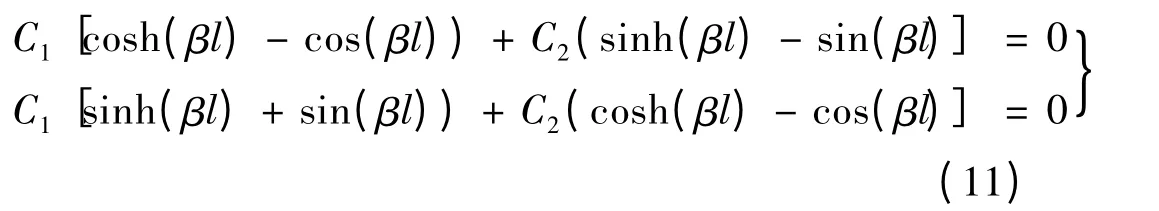
要使C1和C2有非零解，必須使式(11)的系數行列式為0，即:

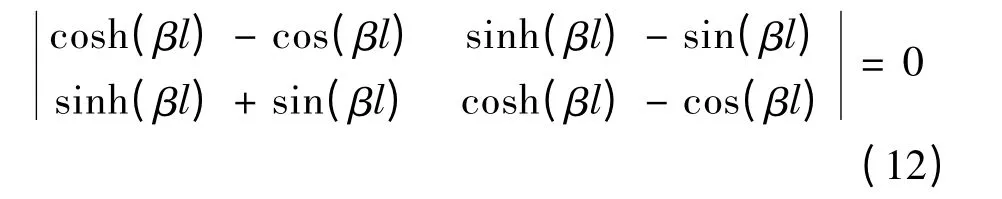
化簡式(12)可得:

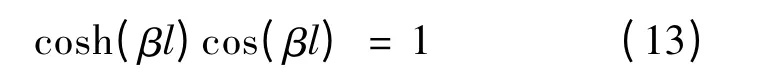
求解式(13)可得β 值，進而可以由式(6)和式(8)求得自由振動的角頻率和對應的模態:

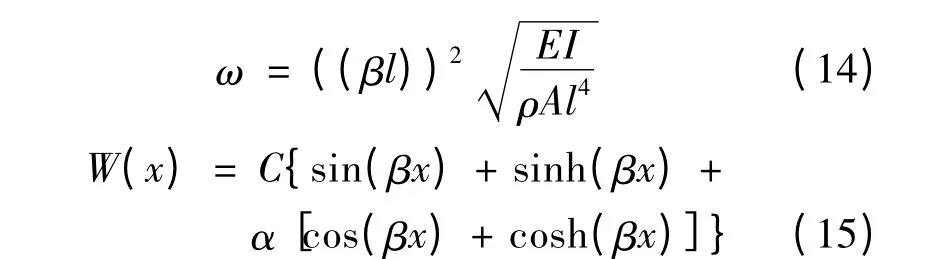
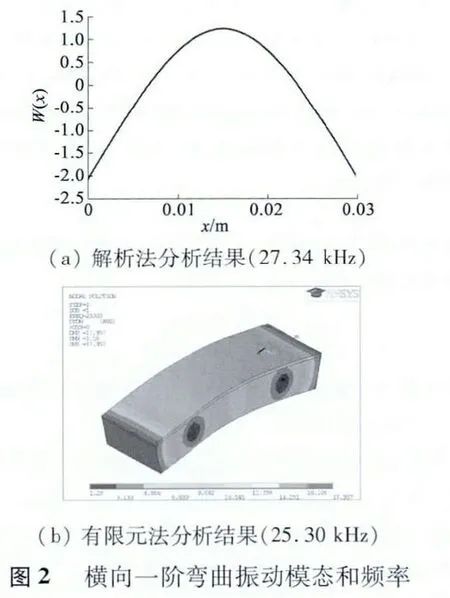
采用建立的解析模型對直線超聲波電動機的振動進行分析。電機金屬彈性體的材料采用鋼，其彈性模量為180 GPa，密度為7 850 kg/m3，壓電陶瓷采用0.5 mm 厚的PZT－502。金屬等直梁的長×寬×高尺寸為30 mm×10 mm×5 mm，忽略PZT 的影響，計算得到金屬彈性體橫向一階彎曲自由振動的頻率為27.34 kHz，對應的振動模態解析法分析如圖2(a)所示。同時也采用有限元分析軟件ANSYS 對該電機進行模態分析，結果如圖2(b)所示，電機的橫向一階彎曲自由振動的頻率為25.30 kHz。解析法和有限元法分析結果存在差異，主要原因在于解析法忽略了PZT 的影響，而有限元法將PZT 也考慮在內了;另外，有限元法分析時建立的是三維實體模型，采用了SOLID5 單元劃分網格，而不是二維梁單元模型，而解析法建立的是二維的等截面梁振動模型。

3 實驗測試

制作的超聲波電動機樣機如圖3 所示。考慮到加工的方便性，金屬彈性體和驅動足是分開加工的，最后將驅動足粘貼在金屬彈性體上。這樣做可以方便地調整兩個驅動足的位置，以研究驅動足粘貼在不同位置時電機的性能。

圖3 駐波型直線超聲波電動機樣機

首先對制作的電機樣機進行阻抗－頻率特性測試，采用美國Agilent 公司的阻抗特性分析儀(型號4294A)，設定掃頻范圍為20 ～50 kHz，結果如圖4所示。圖4(a)為電機未粘貼兩個驅動足時的阻抗－頻率特性，圖4(b)為粘貼上兩個驅動足后的阻抗－頻率特性。粘貼驅動足前，電機的橫向一階彎曲振動的頻率為26. 94 kHz，與理論分析結果接近。粘貼上驅動足后，頻率降為25.15 kHz，說明驅動足對電機的共振頻率有較大的影響。測試結果表明，驅動足的位置越靠近振動節點，對振動頻率的影響越小。

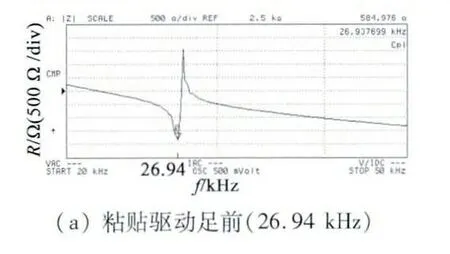
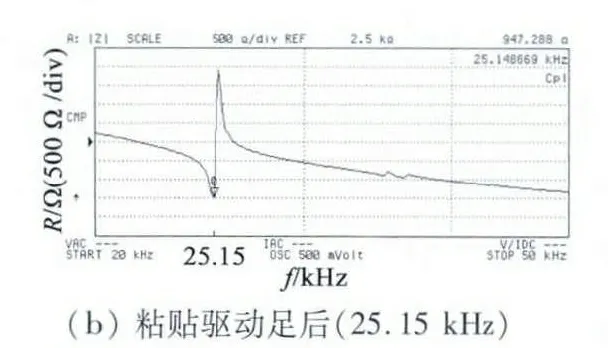
圖4 駐波型直線超聲波電動機的阻抗－頻率特性

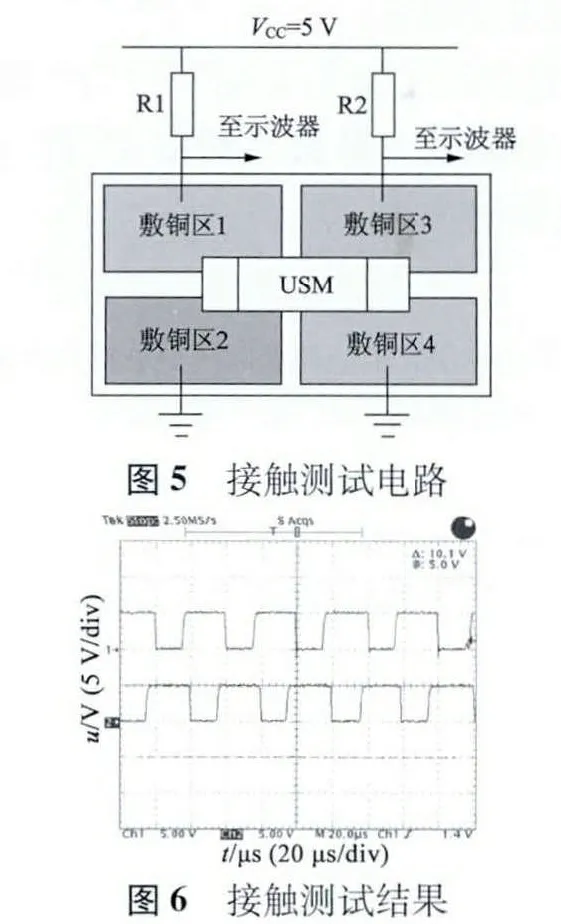
為了解兩個驅動足的驅動狀態，設計了如圖5所示的電路對驅動足進行接觸測試。圖5 中，在印制電路板上設置4 個敷銅區，驅動足1 橫跨在敷銅區1 和2 之間，驅動足2 橫跨在敷銅區3 和4 之間，當驅動足著地時，示波器顯示低電平信號，當驅動足抬離地面時，示波器顯示高電平信號。施加在超聲波電動機上的電壓信號由信號發生器產生正弦電壓信號，經過高頻功率放大器放大后得到，放大后的電壓幅值為15 V，頻率為25 kHz，此時超聲波電動機的行進速度約為4 cm/s。兩個驅動足的接觸測試結果如圖6 所示，每個驅動足與測試電路板接觸的時間約為振動周期的40%，且兩個驅動足與電路板是交替接觸的。通過變換驅動足的位置進行測試表明，驅動足的粘貼位置越靠近振動節點，接觸時間越長，電機行進速度越慢。

4 結 語

本文研究了一種駐波型直線超聲波電動機，建立了電機振動的解析模型，求得電機橫向一階彎曲振動的頻率，同時用有限元法對電機的振動特性進行了分析，制作了電機樣機，并對樣機進行了阻抗－頻率特性測試。測試結果與理論分析的結果相吻合，測試結果也表明，驅動足對電機的共振頻率有影響，驅動足的位置越靠近振動的節點，對振動頻率的影響越小。最后設計了一種電接觸測試的方法，對電機兩個驅動足的接觸狀態進行了實驗研究，結果表明，驅動足越靠近振動節點，與地面接觸的時間越長，電機行進速度越慢。

［1］ LE A Y，MILLS J K，BENHABIB B. Improved linear ultrasonic motor performance with square－wave based driving－tip trajectory［J］. Smart Materials and Structures，2015，24(3):1－7.

［2］ LIU Yingxiang，CHEN Weishan，FENG Peilian，et al. A square－type rotary ultrasonic motor with four driving feet［J］.Sensors and Actuators A:Physical，2012，180:113－119.

［3］ 李霞，張三川，陳維山.三波諧波摩擦傳動超聲波電動機理論研究［J］.微特電機，2011，39(5):1－4，21.

［4］ 彭太江，伍曉宇，梁雄，等.螺旋葉片轉子超聲電機運動特性分析與測試［J］.中國電機工程學報，2014，34(26):4534－4538.

［5］ 謝天，周鐵英，陳宇. 一種雙轉子模態轉換型超聲波電動機的設計［J］.微特電機，2009，37(10):18－21.

［6］ WANG Hongxiang，HU Jing，MA Yuanyuan，et al. Research of a piezoelectric driving linear movement device［J］.Advanced Materials Research，2011，299/300:1099－1102.

［7］ HUANG Weiqing，WANG Yin.A novel ultrasonic motor using longitudinal vibration of bar with varying section［J］.Advanced Materials Research，2012，354/355:527－530.

［8］ 陳強，徐志科，蔣春容，等.雙足驅動雙壓電晶片直線超聲波電動機運行機理研究［J］.振動與沖擊，2014，33(22):21－25.

［9］ WAI Rongjong，SU Kuoho.Supervisory control for linear piezoelectric ceramic motor drive using genetic algorithm［J］. IEEE Transactions on Industrial Electronics，2006，53(2):657－673.

［10］ 李欣業，張明路.機械振動［M］.4 版.北京:清華大學出版社，2009:439－452.