直線電動機動態摩擦力補償和控制方法研究

徐 帥

(包頭鐵道職業技術學院，包頭014160)

式(16)中，k1 ＞0 為增益常數。基于式(13)，對p 求導得:

0 引 言

通常情況下，直線電動機系統具有比較明顯的非線性，主要是由摩擦力、定位力、電磁驅動力等因素造成的［1］。在一些要求不高的運動控制場合，上述非線性因素對系統的影響可以忽略不計;但是若某些運動控制場合對速度或精度的要求較高，就必須將上述非線性因素考慮進去，否則會造成系統的控制性能明顯下降，甚至會出現系統失穩的情況［2］。摩擦力由于其高度的復雜性和不確定性［3］，受到國內外學者廣泛的關注。為準確描述摩擦力特性，許多靜態或動態摩擦力模型如Kanlopp、Armstrong－Helouvry、Dahl、Bristle、LuGre［4－5］被提出并使用。鑒于摩擦力的高度非線性，上述模型本身會比較復雜，如果直線電動機系統的實時補償控制中直接采用這些模型，會造成較多的問題。對于直線電動機驅動系統的摩擦力補償控制，目前已有不少研究成果，但是始終無法在保證模型準確性和補償控制簡易性的前提下，實現高精度的運動控制［6－8］。所以，在這方面仍有不少的上升空間，本文基于改進LuGre 動態模型設計一種直線電動機自適應魯棒控制算法，以減小摩擦力的非線性對系統控制性能的影響。

1 改進LuGre 摩擦力模型

對于靜態摩擦力，其數學模型可表示:

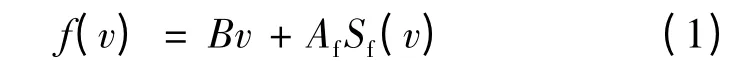
式中:B 為粘滯摩擦系數;Af為庫侖摩擦系數;Sf(v)是庫侖摩擦函數。對于動態摩擦力，其數學模型普遍采用Canudas de Wit 等人提出的LuGre 模型［9］，其數學表達式:

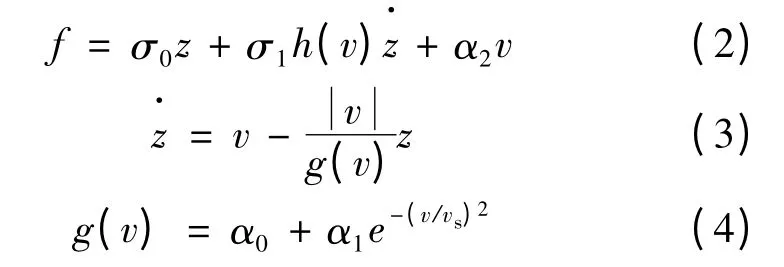
式中:z 為不可測量的內部摩擦狀態;σ0表示剛度;σ1表示阻尼系數;α2則表示粘滯摩擦系數。

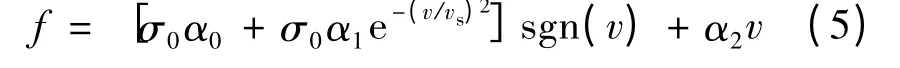
由于內狀態參數z 不可測量，所以動態摩擦力的補償控制中需要加入一個狀態觀測器。根據動態摩擦力的改進LuGre 模型結構，狀態觀測器可以設計:

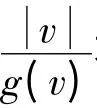
綜上所述，本文提出了一種改進的LuGre 動態摩擦力模型，該模型既適用于低速情況，又適用于高速情況，并且可以在高速和低速之間平滑切換，其數學表達式如下:

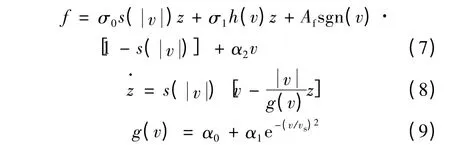
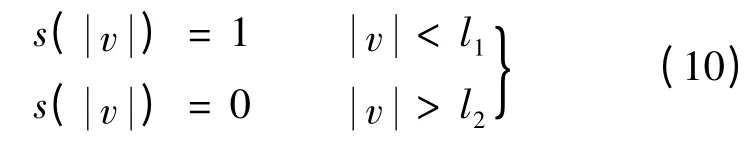
式中:l2＞l1＞0 表示切換速度，主要由數字控制采樣頻率和系統摩擦力特性決定。

從本質上講，改進LuGre 模型在高速情況下可停止內狀態觀測;在低速情況可保證z 為常數，所以z 的狀態估計始終是連續的。這樣就能夠解決原LuGre 模型在數字控制時的不穩定問題，且改進動態摩擦力模型具有以下特性:

2 直線電動機自適應魯棒控制

2.1 問題描述

為減小動態摩擦力非線性對直線電動機系統性能的影響，本文基于改進LuGre 模型，提出了一種自適應魯棒控制算法，用于直線電動機的動態摩擦力補償。那么系統的狀態方程可表示:

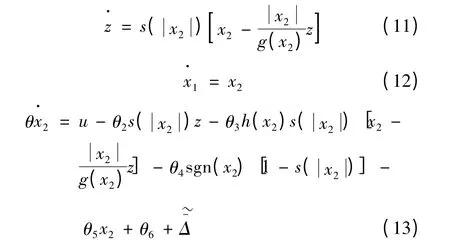
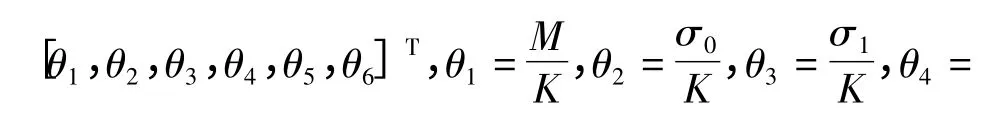
假設1:若參數時變和建模誤差都是已知的，即:

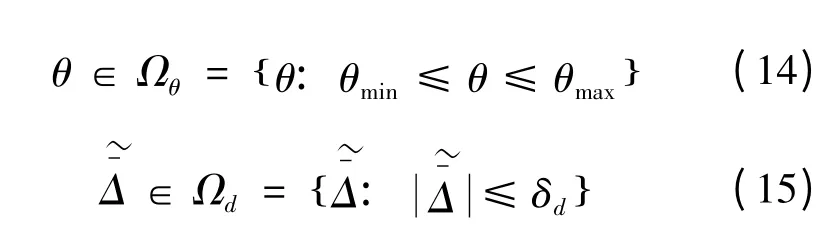
式 中: θmin= ［θ1min，…，θ6min］T， θmax=［θ1max，…，θ6max］T和δd是已知的。

定義xd(t)為有界，且二階可導的參考軌跡，那么控制問題可描述為:在存在各種建模誤差、動態摩擦力模型結構已知而且未知參數滿足假設1 的條件下，設計控制輸入u，使得動力學系統式(11)～式(13)的軌跡跟蹤誤差e 盡可能小。

2.2 自適應魯棒控制

定義一個類滑模變量p［11］:

式(16)中，k1＞0 為增益常數。基于式(13)，對p 求導得:

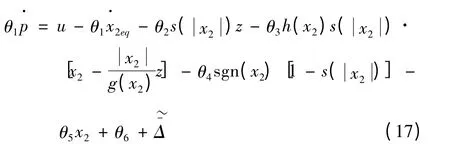
考慮到參數z 的不可測量性，可設計一種基于映射函數的雙重觀測器［12］，保證系統對建模誤差的魯棒性:

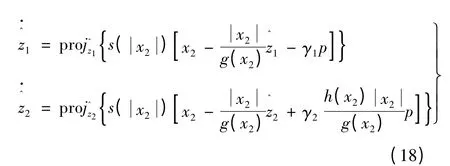
式(18)中的不連續映射函數定義:

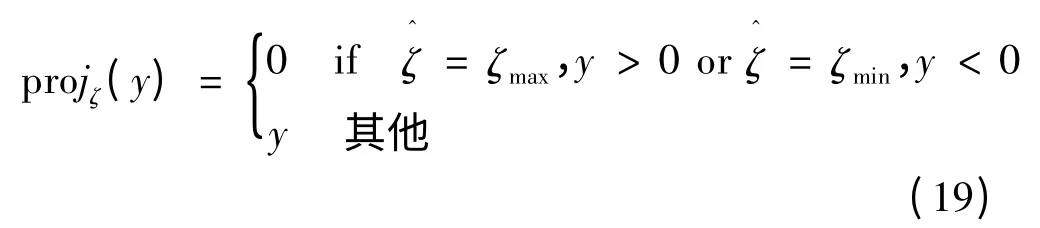
式中:ζ 表示z1或z2;y 表示任意函數;觀測器上界為z1max=z2max=α0+α1，觀測器的下界為z1min=z2min=－α0－α1。此外，對于參數的在線估計，投影式自適應律可設計:

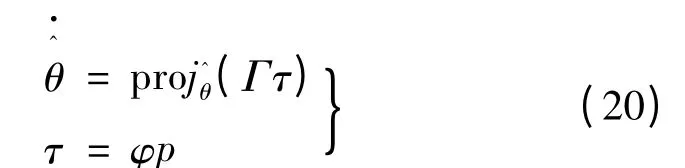
自適應魯棒控制器［13］可設計:

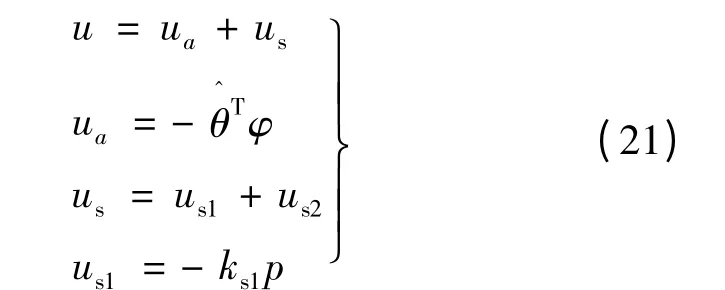
式(21)中，ua是自適應模型補償項;us為魯棒反饋項;us1為比例反饋;us2為魯棒反饋項，其滿足以下兩個條件:

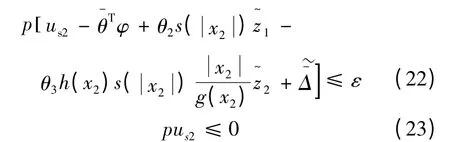
式中:ε 為一任意小的常數。

3 實驗研究

直線電動機精密運動控制系統選用Rockwell公司的兩軸直線電動機驅動平臺，主要由直線電動機、電機驅動器、光柵尺和直線導軌組成，控制系統具體結構如圖1 所示。其中平臺使用Anorad 的無刷直流直線電動機，具體參數如表示1 所示。

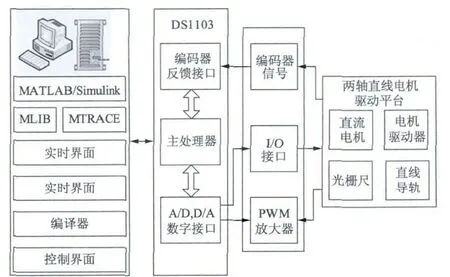
圖1 直線電動機精密運動控制系統

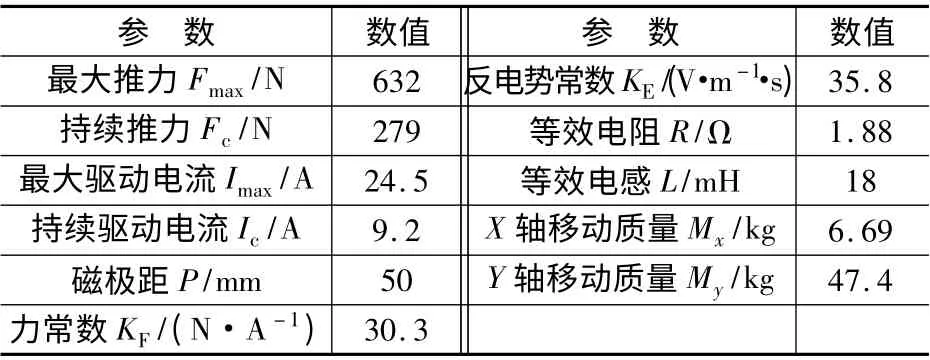
表1 電機主要參數

以兩軸直線電動機平臺的X 軸直線電動機作為研究對象，對比以下兩種算法:(1)基于靜態摩擦力補償的自適應魯棒控制算法;(2)基于改進LuGre動態摩擦力補償的自適應魯棒控制算法。分別進行低速和高速實驗。各控制參數分別為:k1=250，γ1=γ2=0.2，(0)=［0.12，7000，1176，0.15，0.166，;參數變化的上下界選為θmax=［0.2，10 000，1 500，0.3，0.5，0.5］T和θmin=［0.1，4 000，500，0. 1，0，－ 0. 5］T;對 于 低 速 實 驗Γ = diag{1，2.5 ×1010，2.5 ×108，100，10，1 000 }，高 速 試 驗中Γ=diag {1，2.5 ×1010，10 000，100，10，2 000 }。

3.1 低速實驗

在低速實驗中，參考軌跡xd(t)可定義:位移s=0.001 m，速度vmax=0.000 2 m/s，加速度Amax=0.000 2 m/s2的點到點軌跡。由于直線電動機的運動范圍較小，所以可以忽略定位力的影響。低速實驗的跟蹤誤差如圖2 所示。

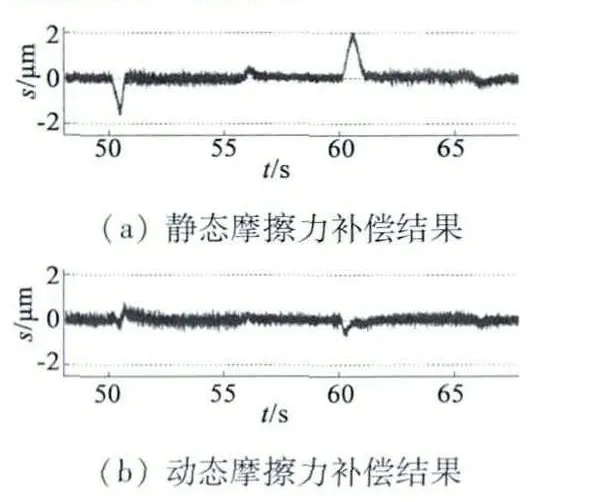
圖2 低速運動跟蹤誤差

由實驗結果可知:當速度的大小或方向發生變化時，動態摩擦力對直線電動機的控制性能影響較大。基于算法(1)得到的軌跡跟蹤誤差，其最大值為2 μm;而基于算法(2)卻可以將軌跡跟蹤最大誤差控制在700 nm，在一定程度上降低了系統跟蹤誤差，驗證了基于改進LuGre 模型的直線電動機動態摩擦力補償方法的有效性。

3.2 高速試驗

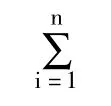
4 結 語

本文針對直線電動機系統中摩擦力的非線性問題，建立了改進LuGre 動態摩擦力模型，并結合自適應魯棒控制技術，提出了一種基于改進LuGre 模型的直線電動機動態摩擦力補償方法，同時設計了一種穩定的不可測內狀態觀測器，實驗結果驗證了所述模型補償和自適應控制算法的有效性。

［1］ ALTINTAS Y，VERL A，BRECHER C，et al.Machine tool feed drives［J］.Annals of the CIRP，2011，60(2):779－796.

［2］ 吳紅星，錢海榮，劉瑩，等. 永磁直線同步電機控制技術綜述［J］.微電機，2011，44(7):76－80.

［3］ 李義強，周惠興，王先逵，等.直線電動機伺服定位系統時間最優魯棒控制［J］.電機與控制學報，2011，15(3):13－18.

［4］ LIU Z，LUO F，RASHID M.Robust and precision motion control system of linear motor direct drive for high speed X－Y table positioning mechanism［J］.IEEE Transactions on Industrial Electronics，2005，52(5):1357－1363.

［5］ 陳淵睿，吳捷，CHEUNG N C.永磁直線電動機的模型參考自適應控制［J］.華南理工大學學報，2003，31(6):31－35.

［6］ WIT C C，OLSSON H，ASTROM K J，et al.A new model for control of systems with friction［J］. IEEE Transactions on Automatic Control，2000，40(3):419－425.

［7］ SWEVERS J，AL－BENDER F，GANSEMAN C，et al.An integrated friction model structure with improved presliding behaviour for accurate friction compensation［J］. IEEE Transactions on Automatic Control，2000，45(4):675－686.

［8］ FREIDOVICH L，ROBERTSSON A，SHIRIAEV A，et al. Friction compensation based on LuGre model［C］//Proceedings of 45th IEEE conference on decision and control，San Diego，CA，2006，3837－3842.

［9］ BONA B，INDRI M，SMALDONE N.Rapid prototyping of a modelbased control with friction compensation for a direct－drive robot［J］.IEEE/AS ME Transactions on Mechatronics，2006，11(5):576－584.

［10］ JAMALUDIN Z，BRUSSEL H，SWEVERS J.Friction compensation of an xy feed table using friction－model－based feedforward and an inverse－model－based disturbance observer［J］. IEEE Transactions on Industrial Electronics，2009，56(10):3848－3853.

［11］ XU L，YAO B. Adaptive robust control of mechanical systems with nonlinear dynamic friction compensation［J］. International Journal of Control，2008，81(2):167－176.

［12］ LEE T，TAN K，HUANG S. Adaptive friction compensation with a dynamical friction model［J］. IEEE/ASME Trans. on Mechatronics，2011，16(1):133－140.

［13］ ARMSTRONG－HELOUVRY B，DUPONT P.Friction modeling for controls，and compensation techniques for servos with friction［C］//Proceedings of American Control Conference，1993:1905－1915.