基于MRAS 的內置式永磁同步電機無傳感器控制

張洪宇

(中國科學院 長春光學精密機械與物理研究所，長春130033)

定義η(0，t1)=η1 +η2，則:

0 引 言

永磁同步電動機(以下簡稱PMSM)根據其轉子永磁體安裝位置的不同，可以分為兩類［1］:表面式永磁同步電動機(以下簡稱SPMSM)和內置式永磁同步電動機(以下簡稱IPMSM)。二者的主要區別體現在IPMSM 有明顯的磁阻轉矩，交軸電感大于直軸電感，SPMSM 無明顯的磁阻轉矩，交、直軸電感相等，這樣的不同將在控制算法上引起一定的差別。永磁同步電機矢量控制中轉子速度與位置是必不可少的反饋信息，通常可由多種編碼器獲得，但由于成本、安裝、維護、干擾等問題的存在，促使了旨在解決電機系統中無編碼器的永磁同步電機無傳感器控制的研究。目前一些文獻［2－14］已經分別提出多種轉子速度與位置估算方法，這些方法雖然存在具體實現手段上的差異，但仍然可以主要分為以下幾種:對于SPMSM，有基于定子磁鏈并利用電機反電動勢估算的反電勢法［2－3］，基于滑模變結構理論的滑模觀測器法［4－5］，采用遞推濾波方法實現估算的擴展卡爾曼濾波器法［6－7］，利用線性或非線性電機相關參數狀態反饋的狀態觀測器法［8－9］，以及基于模型參考自適應控制的方法［10－11］。而對于IPMSM，由于存在交、直軸電感不相等的情況，電機數學模型變得復雜，使得速度與位置的估算更為復雜，方法上受到一定限制。文獻［12］提出一種基于鎖相環配合電機狀態觀測器的方法，實現了對IPMSM 的無位置傳感器控制，具有實用參考價值;而文獻［3］所提出的基于反電勢的估算方法是既適用于SPMSM 也適用于IPMSM 的;此外，文獻［13－14］利用IPMSM 的凸極特性，采用高頻注入電壓或電流信號獲得轉子位置和速度信息;而擴展卡爾曼濾波器法、滑模觀測器法以及模型參考自適應法由于在IPMSM 上實現的復雜性而鮮有提及。

本文著眼于IPMSM 的無位置傳感器控制研究，將模型參考自適應(以下簡稱MRAS)算法實現于對IPMSM 的轉子速度與位置估算;以電機本身作為參考模型，電機電流方程為可調模型，算出較為復雜的自適應律，并給出相應證明;基于MATLAB/Simulink建模，仿真驗證MRAS 算法對IPMSM 轉子速度與位置估算的效果，另搭建實驗系統，驗證可行性。

1 模型參考自適應系統

模型參考自適應系統通常由參考模型、可調模型和自適應律三部分組成。其中參考模型指的是不含有待估計參數的方程，而可調模型指的是含有待估計參數的方程，兩模型同時工作，二者的輸出量具有相同物理意義，利用兩模型輸出量偏差，通過合適的自適應律調節可調模型參數，使系統達到穩態時偏差趨于零，從而實現可調模型跟隨參考模型。圖1 為本文采用的并聯型模型參考自適應系統，此外還有串聯型和串、并聯型等。

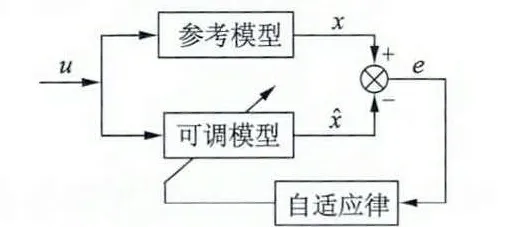
圖1 并聯型模型參考自適應系統

對于PMSM 轉速估算模型參考自適應系統，本文將采用PI 控制為自適應機制，基于Popov 超穩定性和正實性動態系統理論設計自適應律，確保自適應機制穩定收斂。

2 IPMSM 速度與位置估算

2.1 參考模型與可調模型的建立

構建PMSM 轉速估算的并聯型模型參考自適應系統，將以IPMSM 本身作為參考模型，電機的電流方程作為可調模型。

在d－q 旋轉坐標系下，IPMSM 的電流方程表示:

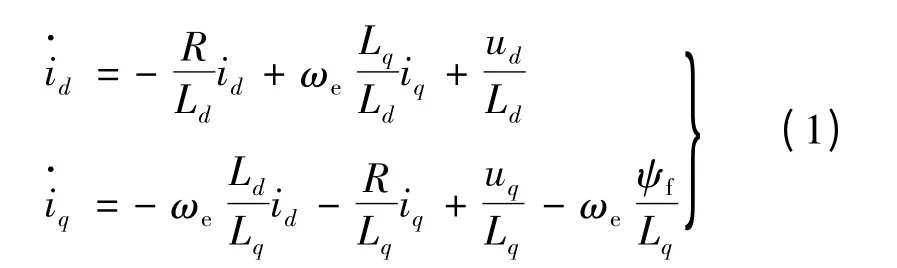
式中:id，iq，ud，uq分別為d－q 旋轉坐標系下定子電流和電壓分量;R 為定子電阻;Ld為定子直軸電感;Lq為定子交軸電感;ψf為轉子永磁體磁鏈;ωe為電機轉子電角速度。

可以看出，d－q 旋轉坐標系下的PMSM 電流方程中含有待估算的電機轉速，這也是將電流方程作為可調模型的原因。

將式(1)改寫成矩陣形式并進行適當變換，可以得到如下方程:

式(2)可以簡寫:

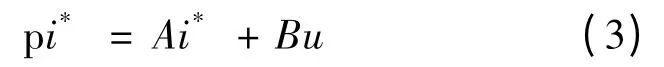
當式(2)中所有參數電流、電壓、轉速等視為電機本身已知真實值時，則式(3)為建立的參考模型。

根據并聯模型參考自適應系統原理(見圖1)，在基于IPMSM 電流數學模型建立的估算系統中，d－q 旋轉坐標系下定子電壓u 為參考模型與可調模型共同的輸入量，定子真實電流i 為參考模型輸出量，定義可調模型觀測電流為可調模型輸出量，待估算轉子電角速度為可調參數，則可調模型矩陣方程構建如下:

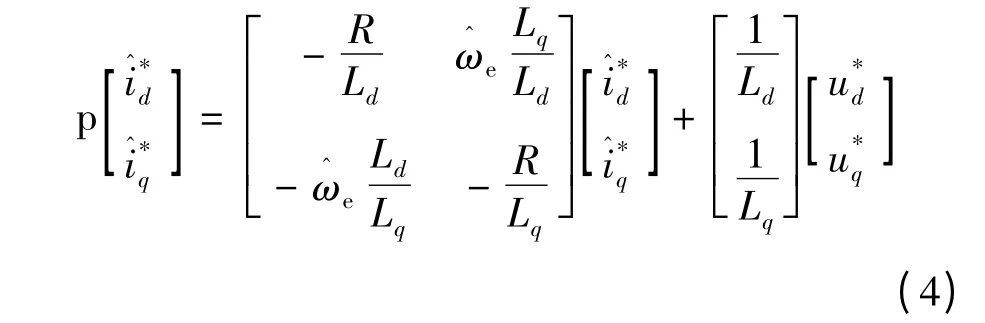
方程(4)簡寫:

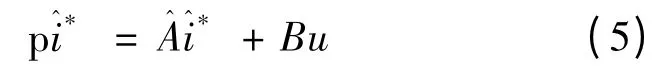
至此，已經分別建立了IPMSM 模型參考自適應系統的參考模型和可調模型。

2.2 自適應律的建立

模型參考自適應系統中，自適應律的作用在于根據參考模型與可調模型的輸出偏差，調節系統中的待估算參數，以使自適應系統穩定且趨于收斂，本文對自適應律的設計方法基于Popov 超穩定性理論，該理論的控制系統結構如圖2 所示的非線性時變反饋系統。

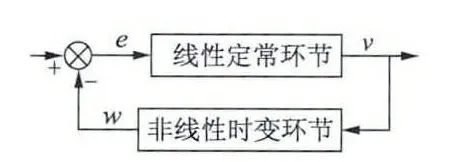
圖2 非線性時變反饋系統

基于參考模型與可調模型偏差構建上述非線性時變反饋系統，并滿足Popov 超穩定性理論就可獲得穩定的自適應律。

參考模型與可調模型的偏差:e =i*－，定義ΔA=－A，則式(3)與式(5)相減可得到下式:

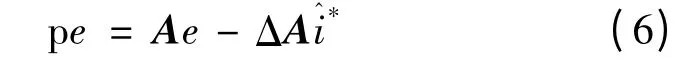
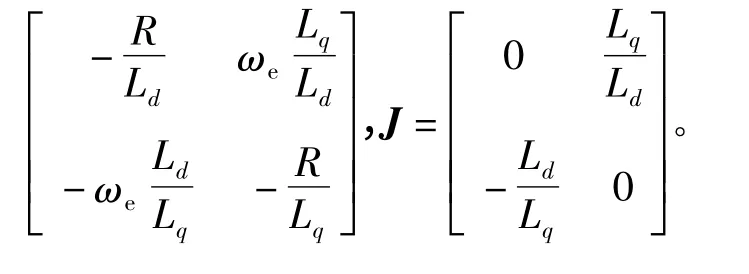
式(6)為非線性時變環節。再構建線性定常環節v=Ce，可以簡單地設定矩陣C 為單位矩陣I，設w=ΔAi^*，這樣就構建了基于模型參考自適應的非線性時變反饋系統方程:

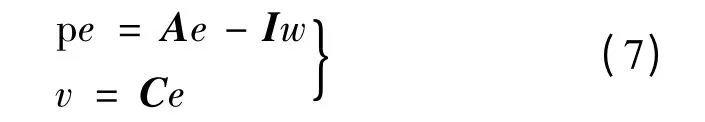
根據Popov 超穩定理論，要想使模型參考自適應系統趨于穩定，上述非線性時變反饋系統方程要滿足以下兩個條件:

1)線性定常環節的方程傳遞函數必須是嚴格正實的，即G(s)=C (sI－A)－1嚴格正實。傳遞函數展開后可得具體形式如下:

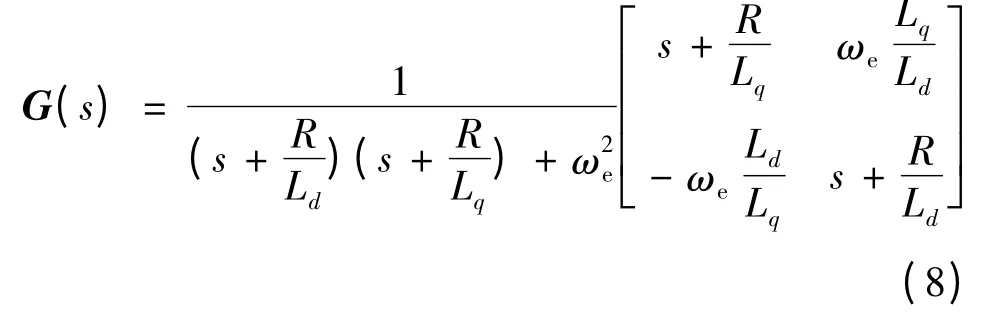
對上式進行矩陣運算后，容易證得該矩陣是正定Hermite 矩陣。再由正實性判定定理，可以進一步證得該傳遞函數G(s)具有嚴格的正實性。

2)對于非線性時變環節，則必須滿足Popov 積分不等式:

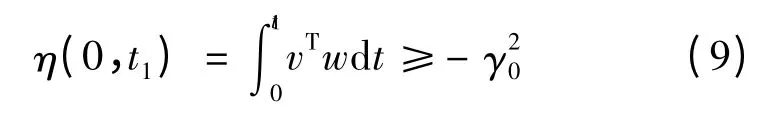
式中:γ0是一個有限大小的正常數，并且與時間t1無關。本文采取PI 控制作為自適應機制，因此可設:

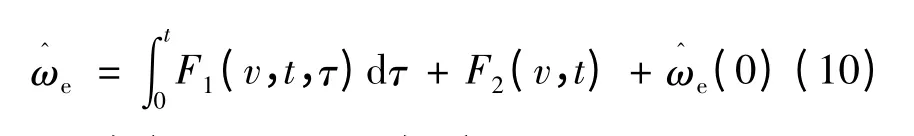
將式(9)展開并將式(10)代入，可得:

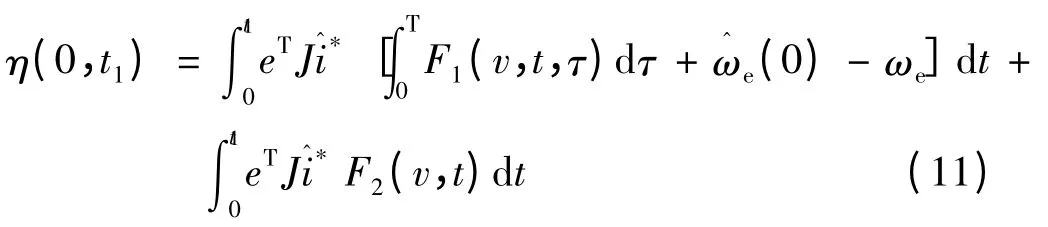
定義η(0，t1)=η1+η2，則:

設:

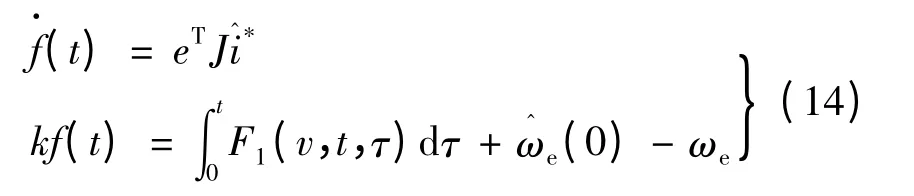
可以證明得到下式:

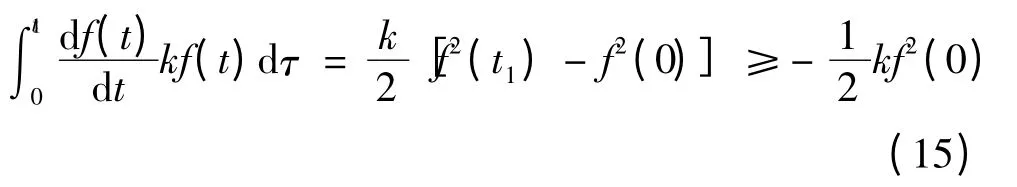
式中:k ＞0，則η1≥－;同理可證η2≥－，進而證明η(0，t1)≥－，即證得該系統滿足Popov 積分不等式。

這樣該系統滿足上述兩個條件，則基于IPMSM所建立的模型參考自適應系統是趨于穩定的。

2.3 轉速與位置估算

求解式(14)可得F1(v，t)=k1eTJi^ * ，同理也可算得F2(v，t)=k2eTJi^ * ，將上述兩結果代入式(10)并完全展開，便可以獲得由自適應律參與調節的電機轉子轉速估計:

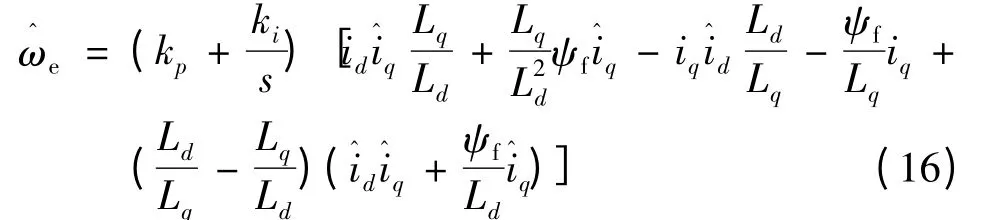
而轉子位置角度可以由速度積分獲得:

3 仿真分析

為驗證前文所述對IPMSM 采用模型參考自適應估算轉速和位置的理論的有效性，將采用MATLAB/Simulink 對如圖3 所示的基于模型參考自適應的IPMSM 無位置傳感器矢量控制原理框圖進行建模仿真，分析估算效果。

圖3 IPMSM 無傳感器矢量控制框圖

本文所采用的IPMSM 相關參數如表1 所示，仿真與實驗皆基于此電機進行。

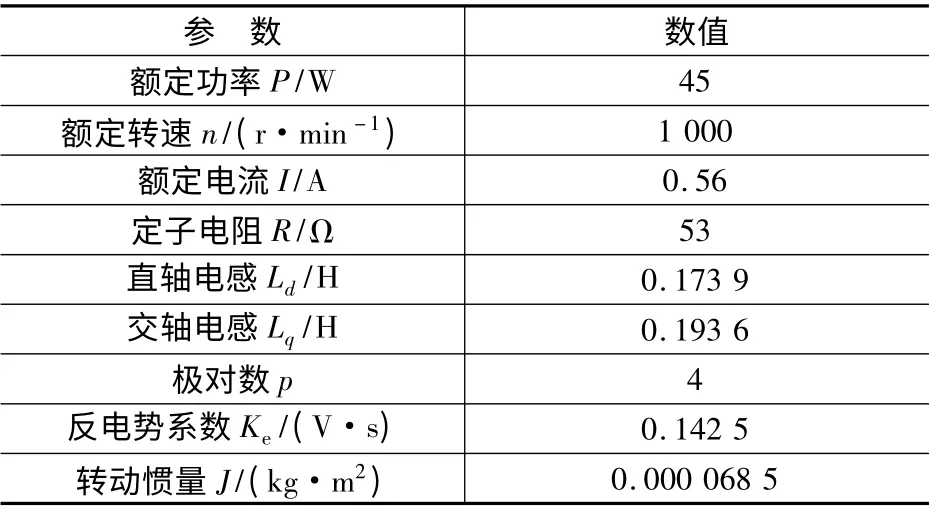
表1 IPMSM 參數

下面重點給出MRAS 部分的仿真建模模型，而控制系統的其它部分由于不是本文重點將不會給出詳細的建模模型。圖4 為可調模型電流觀測建模，即獲得觀測電流與。圖5 則是由觀測電流進一步根據式(16)與式(17)完成轉速與位置估算的建模。

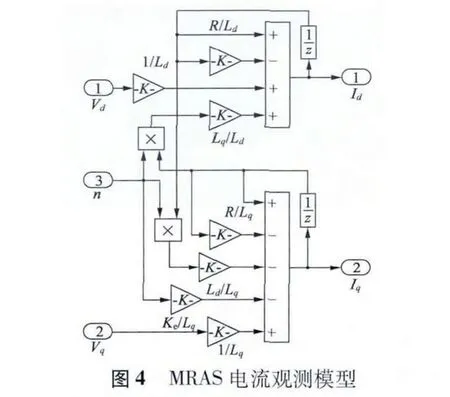
圖5 MRAS 轉速與位置估算模型

在PMSM 無位置傳感器控制中，電機的起動是另一大難題，本文試圖簡化這一難題，采用定位后拖轉電機到一定轉速再切入閉環控制的方法。圖6 為本文電機起動部分的u 相電流仿真波形，0 ～1 s 階段是對轉子的定位，1 ～9 s 階段為拖轉，定位與拖轉電流為1.5 A，拖轉轉速設定為300 r/min，9 s 以后切入閉環，閉環設定轉速為600 r/min，設定負載為0.1 N·m。可見，切入閉環MRAS 工作后，電機電流很快降低到很小值，這是由于拖轉時電流利用率極低，而進入閉環后，MRAS 控制系統將電流利用率提升到最佳范圍，得到較好的控制效果。

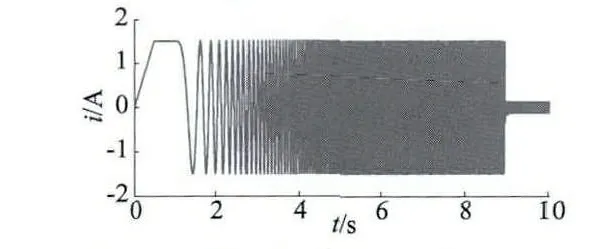
圖6 IPMSM 起動電流

為驗證速度變化時系統響應效果，在第15 s 時負載0.1 N·m 不變，速度由600 r/min 階躍提升為1 000 r/min，速度仿真及相應誤差波形如圖7 所示。角度仿真及相應誤差波形如圖8 所示。從仿真速度曲線可以看出，系統的速度控制響應較快，對于階躍式的速度變化輸入，可以控制電機迅速達到目標速度值，并且保證估算速度跟隨實際速度精準，通過誤差曲線可以看出，階躍響應到達目標值后有一定抖動，速度估算值相對實際速度有一定滯后，導致在階躍變化處，誤差有一定程度地增大式抖動，但隨著系統響應階躍輸入后的穩定，誤差也重新回到平穩且趨于零的狀態。從角度估算及其誤差曲線更可以看出，角度估算的抖動是更小的，僅在階躍變化處有短時間滯后，隨后很快恢復穩定估算跟隨實際角度，角度估算平穩是確保系統控制穩定的重要原因。可見本文構建系統對速度變化響應較快且估算精準。

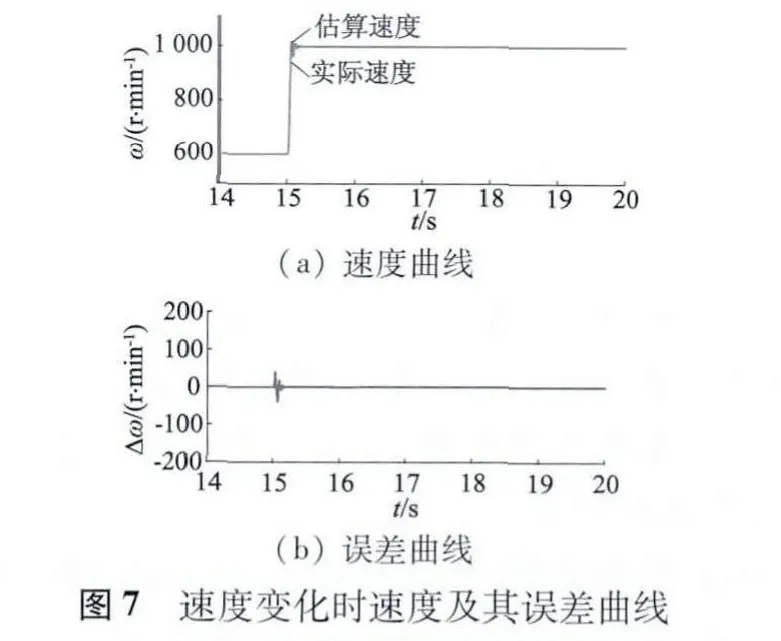
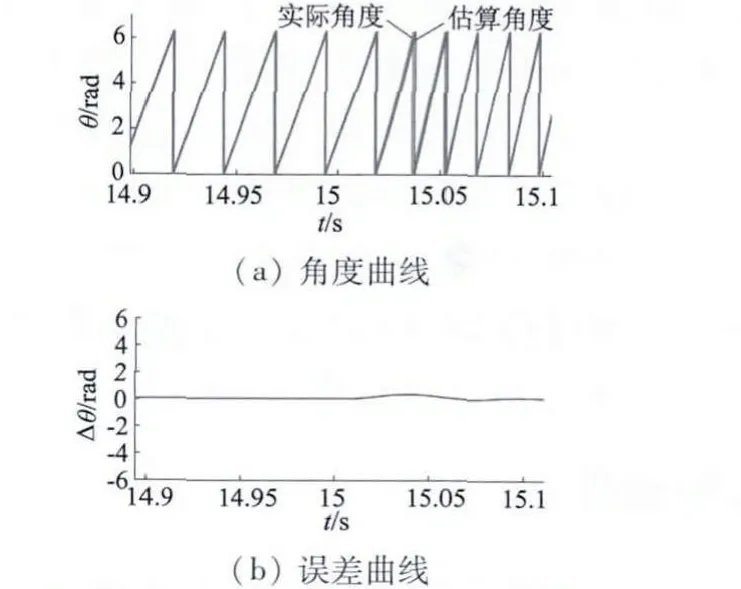
圖8 速度變化時角度及其誤差曲線

為驗證負載變化時系統響應效果，在第15 s 時速度600 r/min 保持不變，負載由0.1 N·m 階躍提升至0.2 N·m，速度仿真及相應誤差波形如圖9 所示。角度仿真及相應誤差波形如圖10 所示。從速度仿真波形可以看出，由于瞬時加大負載，導致電機速度有一次階躍跌落，系統對負載突變響應劇烈，這與系統本身屬于調速控制有關，但另一方面，系統響應依然是迅速有效的，估算速度依然較為精準地跟隨實際速度，從而控制系統速度重新回到目標值。通過相應的誤差曲線可以看出，負載突變處有較大的誤差波動，且持續時間長于速度突變情況，但最終系統仍然能夠自適應調整回穩定且誤差趨于零的狀態。可見本文構建系統具有較強的抗突變、抗干擾能力，魯棒性較強。

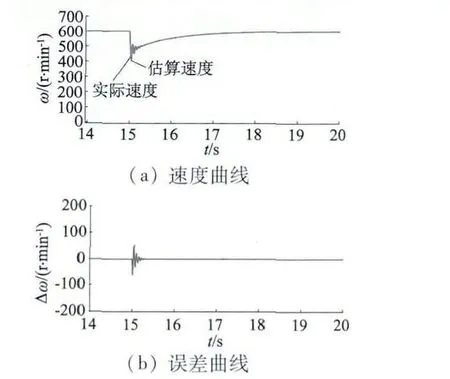
圖9 負載突變時速度及其誤差曲線

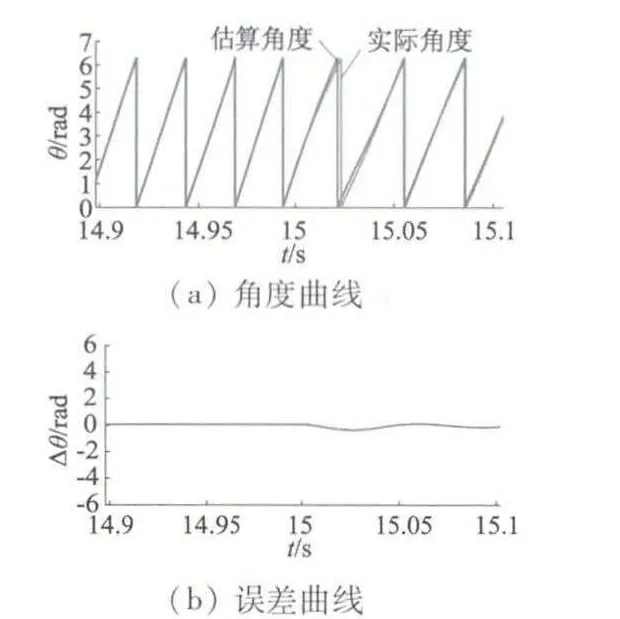
圖10 負載突變時角度及其誤差曲線

仿真結果表明，本文所述MRAS 對IPMSM 的轉速與角度估算動態響應快，在負載或轉速突變時能較快跟隨實際轉速與角度，在穩態過程中估算穩定且平滑。由各誤差曲線可以看出，系統的估算響應僅在條件突變時有短時間輕微抖動，穩態過程中誤差很小，跟隨實際值性能較好，因此本文針對IPMSM 所提出的MRAS 轉速與角度估算系統，估算精度較高，抗干擾能力較強。

4 實驗結果

為進一步驗證該MRAS 對IPMSM 的轉速與角度估算的可行性，針對表1 電機進行實驗研究，證明該系統是否能確保電機真實運轉。

圖11 為電機起動部分的示波器電流波形。其橫坐標為時間，單位1 s/div，放大后單位50 ms/div;縱坐標為電流，單位500 mA/div。可以清楚看到電機切入閉環即MRAS 開始工作時的電流變化，與仿真波形圖6 相比，幾乎完全相同，證明本文起動方法的可行性。不過這一起動方法實現的前提在于電機負載較小或空載，且對轉子初始位置無特殊要求。

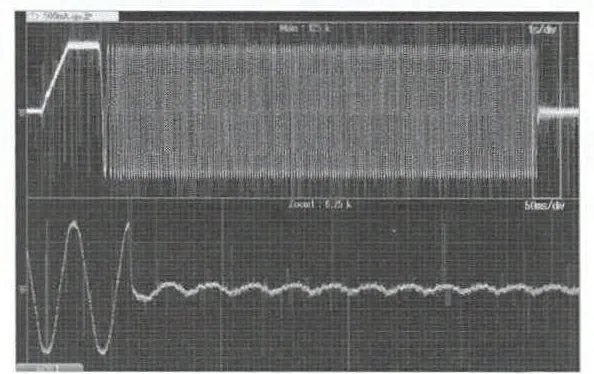
圖11 電機起動電流

圖12 為電機轉速由600 r/min 提升為1 000 r/min 后的示波器電流波形。其橫坐標為時間，單位20 ms/div，放大后單位5 ms/div;縱坐標為電流，單位200 mA/div。從電流波形的周期可以大致算出，此時的電機轉速為1 000 r/min，達到了目標速度，并且系統運行穩定。

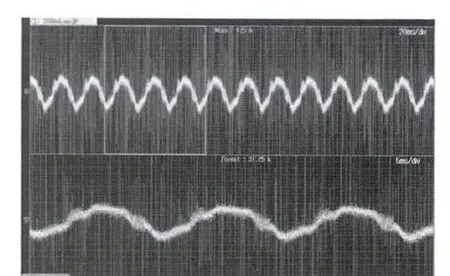
圖12 1 000 r/min 時電機電流

圖13 為電機維持在600 r/min 時增加負載后示波器電流波形。其橫縱坐標與圖12 相同，可以看出，電流幅值比增加負載前明顯增大，通過電流周期可算出，電機速度為600 r/min，系統運行穩定。

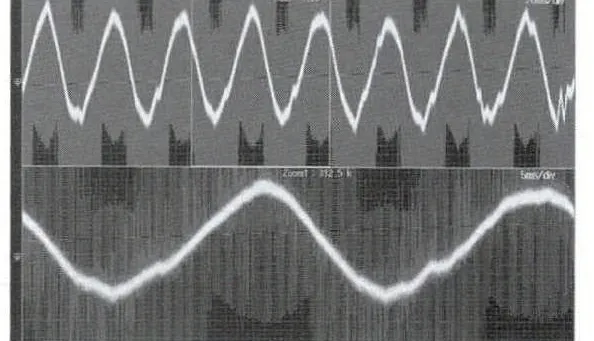
圖13 負載增大時電機電流

根據示波器電流波形，電機起動切入閉環過程的電流波形(圖11)，轉速提升至1 000 r/min 時的電流波形(圖12)，以及在600 r/min 時增大負載后的電流波形(圖13)，可以看出，系統能夠保證電機在各個狀態下穩定運轉，證明本文所述MRAS 對IPMSM 的轉速與角度估算的可行性。

5 結 語

本文實現了針對IPMSM 采用MRAS 的轉速與角度估算，建立無位置傳感器控制系統。完成MRAS 理論分析，并進行仿真實驗，結果表明本文所述系統對IPMSM 的轉速與位置估算精度較高，對速度變化與負載擾動穩定性較強，證明了所述系統的可行性。

［1］ MOHAMED A S，ZAKY M S，ZEIN EI DIN A S，et al.Comparative study of sensorless control methods of PMSM drives［J］.Innovative Systems Design and Engineering，2011，2(5):44－66.

［2］ 陳寧，陳文祥，喻壽益.表貼式永磁同步電機無位置傳感器控制［J］.控制工程，2012，19(2):191－194.

［3］ GRNDUSO F，MICELI R，RANDO C，et al. Back EMF sensorless－control algorithm for high – dynamic performance PMSM［J］.IEEE Trans. on Industrial Electromics，2010，57(6):2092－2100.

［4］ KIM H，SON J，LEE J.A high－speed sliding－mode observer for the sensorless speed control of a PMSM［J］. IEEE Trans. on Industrial Electromics，2011，58(9):4069－4077.

［5］ QIAO Zhaowei，SHI Tingna，WANG Yingdong，et al.New slidingmode observer for position sensorless control of permanent－magnet synchronous motor［J］. IEEE Trans. on Industrial Electronics，2013，60(2):710－719.

［6］ QUANG N K，HIEU N T，HA Q P. FPGA－based sensorless PMSM speed control using reduced－order extended kalman filters［J］.IEEE Trans. on Industrial Electronics，2014，61(12):6574－6582.

［7］ 肖曦，王偉華，呂志鵬.一種基于增量式卡爾曼濾波器的PMSM轉速濾波算法［J］.電機與控制學報，2014，18(10):104－111.

［8］ 祝曉輝，李穎暉.永磁同步電機高增益速度觀測器設計與仿真研究［J］.系統仿真學報，2007，19(11):2550－2554.

［9］ PREINDL M，SCHALTZ E.Sensorless model predictive direct current control using novel second－order PLL observer for PMSM drive systems［J］.IEEE Trans. on Industrial Electronics，2011，58(9):4087－4095.

［10］ FAN Shicai，LUO Wuqiao，ZOU Jianxiao，et al. A hybrid speed sensorless control strategy for PMSM based on MRAS and fuzzy control［C］//IEEE 7th International Power Electronics and Motion Control Conference，2012:2976－2980.

［11］ 呂華芬，葉云岳.基于MRAS 的低速永磁同步電機無位置傳感器控制［J］.機電工程，2012，29(3):307－310.

［12］ 孫承波，宋丹，陳國呈，等. 基于鎖相環的空調直流壓縮機矢量控制系統［J］.電工技術學報，2009，24(4):78－84.

［13］ 金光哲，徐殿國，高強，等. 高頻注入電壓預估同步電機轉子位置檢測方法［J］.中國電機工程學報，2014，34(9):1376－1381.

［14］ ACCETTA A，CIRRINCIONE M，PUCCI M，et al.Sensorless control of PMSM fractional horsepower drives by signal injection and neural adaptive－based filtering［J］. IEEE Trans. on Industrial Electronics，2012，59(3):1355－1366.