永磁同步電機多電機同步控制策略

金 花 寧 濤

(大連交通大學軟件學院，遼寧 大連 116045)

永磁同步電機(PMSM)由于轉子結構采用永磁體替代了異步電機勵磁繞組的機構，降低了轉子的發熱問題，并且由于永磁同步電機體積小、功率因數高、密度高及低速轉矩大等優勢逐漸被應用在需要高速運行、負載變化大和短時工作制的領域，同時使得在PMSM上采用全封閉結構和直驅控制方式成為了可能。但是由于永磁同步電機自身結構對同步性的要求，每臺電機需單獨配備一套牽引變流器，并且與異步電機存在轉速、轉差不同，PMSM對轉速同步性要求較高，電機之間轉速差過大會使擦輪嚴重，如果控制不當，會降低傳動系統的性能[1～3]。因此，筆者針對以上問題提出一種多電機同步控制策略。

1 永磁同步電機簡介①

多電機同步控制是指系統中的電機按照相同轉速運行，并且轉速變化是同步的[4,5]。目前多電機同步控制策略主要有并行控制方式、主從控制方式、虛擬總軸控制方式、交叉耦合控制方式及偏差耦合控制方式[6]等。

PMSM的物理結構如圖1所示。

建立數學模型之前，先做如下假設：

a. 忽略鐵心飽和，不計渦流和磁滯損耗；

b. 永磁材料的電導率為零；

c. 轉子上沒有阻尼繞組。

相繞組中感應電動勢的波形為正弦波。那么基于dq軸旋轉坐標系下的PMSM的數學模型為：

(1)

(2)

(3)

(4)

式中id、iq——d、q軸初級電流；

J——轉動慣量；

Ld、Lq——d、q軸初級電感；

p——電機極對數；

Rs——初級等效電阻；

Te、TL、T0——電磁轉矩、負載轉矩和空載轉矩；

ud、uq——d、q軸初級電壓；

ψd、ψq——d、q軸初級磁鏈；

ψf——永磁體有效磁鏈；

Ωr——轉子機械角速度。

2 基于單神經元偏差耦合多電機控制

2.1 單神經元PID控制器設計

單神經元PID控制器(圖2)具有自學習和自適應能力，其結構簡單、環境適應能力強，并且具有較強的魯棒性，是對傳統PID控制的一種改進和優化[7]，可根據被控對象參數變化進行自適應調節，在一定程度上解決了控制對象復雜和參數慢時變對系統控制上的不足。

圖2 單神經元PID控制結構框圖

圖2中，xi(k)(i=1，2，3)為神經元的3個輸入量，反映的是期望輸出和系統給定的偏差狀態。在此，將系統給定設為y*(k)，實際輸出為y(k)，兩者的偏差為e(k)，x1(k)、x2(k)、x3(k)是偏差e(k)經過狀態變換器，變換成神經元學習進行控制所需要的狀態，性能指標為：

(5)

神經元PID的輸出信號u(k)為：

(6)

由式(5)可知，xi(k)(i=1，2，3)分別對應常規PID的P項、I項、D項，改變式(6)中的ωi(i=1，2，3)就相當于改變P、I、D這3個系數，從而形成具有自學習和自調整能力的神經元PID控制器，他們對應的權值分別為ω1(k)、ω2(k)和ω3(k)。筆者采用有監督Hebb學習算法，其神經元的學習過程為：

ωi(k+1)=(1-c)ωi(k)+ηri(k)

(7)

ri(k)=z(k)u(k)xi(k)

(8)

式中c——常數，這里取c=0；

ri(k)——遞進信號；

z(k)——誤差信號，z(k)=e(k)；

η——神經元學習速率，η>0。

因此可得：

(9)

(10)

(11)

其中K為神經元比例系數，K>0；ηP、ηI、ηD分別為比例、積分、微分學習速率。綜合考慮多種運行狀況將ηP、ηI、ηD和K分別設定為0.5、0.3、0和0.2，加權系數ω1(0)、ω2(0)、ω3(0)分別設定為0.3、0.3、0.3。

由于單神經元學習算法不能直接用傳遞函數加以描述，因此筆者采用S函數編寫模型。單神經元PID控制器仿真模型如圖3所示。

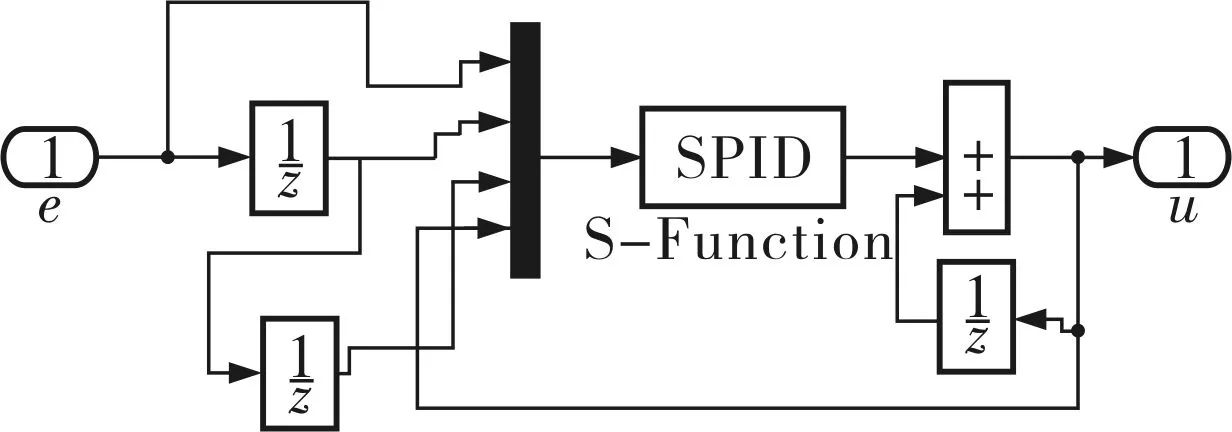
圖3 單神經元PID控制器仿真模型

2.2 偏差耦合控制器設計

電機同步控制方式中的并行控制方式是將各電機進行并聯，每個電機接收的指令來自同一指令單元，這種控制方式適用于結構簡單的系統，即系統采用同型號的電機，能保持各電機轉速同步，但缺點是相對整個系統該控制方式沒有檢測各電機間的轉速差值，因此抗擾動能力弱[8]。

主從控制方式是設定一個主電機，其余電機轉速跟隨主電機轉速進行變化，而主電機不跟隨從電機進行變化，因此這種控制方式適用于電機有明顯主從關系的系統。

交叉耦合控制方式是在并行控制方式的基礎上增加了電機轉速的檢測和反饋。電機之間的轉速跟隨其他電機轉速的變化而變化，但是這種方式經過驗證僅適用于兩臺電機同步控制的場合。

偏差耦合控制方式是在交叉耦合控制方式的基礎上進行了改進，將各個電機轉速反饋值經MUX和DEMUX環節進行整合后，通過轉速補償對電機轉速進行調節(圖4)。筆者利用單神經元PID控制器替代傳統轉速補償，使其更有效地解決被控對象之間的轉速跟隨、過程跟隨及動態性能匹配等非線性問題，更好地實現了多電機間的同步控制。

圖4 基于單神經元PID的偏差 耦合控制系統框圖

筆者采用3臺永磁同步電機進行同步控制研究，同步控制方式采用偏差耦合控制方法，并用單神經元PID控制器代替傳統轉速補償模塊。系統仿真模型為：采集各個電機轉速，經單神經元PID控制器，將調節后的轉速誤差信號與給定轉速進行負反饋后送入PMSM調速系統。

3 系統仿真實驗

筆者利用Matlab7建立了永磁同步電機雙閉環控制系統模型(圖5)，采用有監督Hebb學習算法的單神經元PID控制器，并將其引入到傳統偏差耦合多電機同步控制中，替代了轉速補償模塊。

圖5 單神經元PID偏差耦合多 電機同步控制系統仿真模型

PMSM額定參數為：額定電壓UN=300V，額定頻率fN=100Hz，定子電阻Rs=0.9585Ω，電感Ld=Lq=5.25mH，轉子永磁體磁通ψf=0.1827Wb，電機極對數p=4，摩擦因子F=0.0003035N·m·s。3臺電機轉動慣量分別為：0.6329、0.6429、0.6529g·m2。仿真實驗從以下兩個方面來驗證筆者提出方法的合理性。

圖6 3臺電機的轉速跟隨曲線局部放大曲線

3臺電機在t=0.1s時的同步轉速誤差曲線如圖7所示。

通過圖6、7可以看出，由于采用具有監督Hebb學習方法的單神經元PID控制器替代傳統轉速補償模塊，使得基于改進的偏差耦合多電機同步控制系統具有很強的自調節能力，當轉速突變時，系統超調小、魯棒性強、電機間轉速很快達到同步。

圖7 3臺電機在t=0.1s時的同步轉速誤差曲線

突加負載擾動。電機以n*=1000r/min空載啟動，當t=0.1s時，各電機突加負載TL=3N·m；當t=0.3s時，各電機的負載減少為TL=1N·m。仿真實驗轉速波形和局部放大波形如圖8所示。

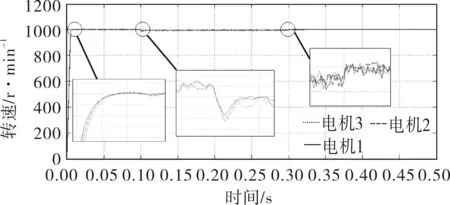
圖8 基于單神經元PID偏差耦合同步 控制3臺電機轉速跟隨曲線

從圖8可以看出，當電機給定轉速空載啟動時，各個電機轉速基本無超調，跟隨性好。當t為0.1、0.3s突然加減負載擾動時，電機間調節時間短、魯棒性好，很快進入同步狀態。

4 結論

4.1由于采用有監督Hebb學習算法的單神經元PID控制器，學習速率ηP、ηI、ηD取值裕度比較大，而根據公式可知增益K取值非常重要，取值偏大會增大系統超調，偏小會增加系統響應時間。

4.2建立了PMSM單神經元PID的偏差耦合控制數學模型，利用Matlab7搭建了系統仿真模型，對轉速突變和突加、減負載兩個方面進行仿真實驗分析，通過實驗結果說明有監督Hebb學習算法的單神經元PID運用到偏差耦合多電機同步控制系統中，使系統具有良好的自適應能力，能夠有效地減小超調甚至無超調，提高系統響應能力，增加系統的魯棒性，充分驗證了筆者提出基于單神經元PID的偏差耦合多電機同步控制方法的合理性。

[1] 劉金琨.先進PID控制MATLAB仿真[M].北京：電子工業出版社，2004.

[2] 張世韜，楊風，郝騫.單神經元PID控制器研究及仿真[J].機械工程及自動化，2009，(3)：69～70.

[3] 侯勇嚴，郭文強.單神經元自適應PID控制器設計方法研究[J].微計算機信息，2005，(12)：8～9，17.

[4] Perez-Pinal F J,Caladeron G,Araujo-Vargas I.Relative Coupling Strategy[C].2003 IEEE International Electric Machines and Drives Conference.USA：IEEE，2003:1162～1166.

[5] 王成元，夏加寬，孫宜標.現代電機控制技術[M].北京：機械工業出版社，2008：128～129.

[6] Miroslav M,Hodder A,Perriard Y.Analysis of the Commutation Currents for a Sinusoidal BLDC Motor[C].2008 International Conference on Electrical Machines and Systems.Wuhan：IEEE，2008: 3016～3019.

[7] 苗新剛，汪芬，韓凌攀，等.基于偏差耦合的多電機單神經元同步控制[J].微電機，2011，44(2)：44～47.

[8] 劉坤.多永磁同步電機同步控制策略的研究[D].長沙：中南大學，2011.

SynchronusControlStrategyforPermanentMagnetSynchronousMulti-motor

JIN Hua, NING Tao

(SchoolofSoftware,DalianJiaotongUniversity,Dalian116045,China)

Considering the characteristics of permanent magnet synchronous motor, the single neuron PID-based deviation coupling synchronization control strategy was proposed and the mathematic model concerned