短幅內擺線型螺桿-襯套副滑動速度分析*
杜秀華 劉雙新 宋玉杰 韓國有
(東北石油大學機械科學與工程學院)
單螺桿式水力機械是石油化工和鉆采機械領域中常用的水力機械,如單螺桿泵、單螺桿鉆具及單螺桿油氣混輸泵等。它們都是依靠一對螺桿-襯套副的嚙合來實現液體傳輸或動力傳遞的,因此螺桿-襯套副的滑動速度是影響其磨損程度和使用壽命的重要因素之一。早在20世紀80年代蘇義腦等就對短幅內外擺線型螺桿-襯套副的線型理論進行了系統的研究,形成了螺桿-襯套副線型的基本理論[1~3]。20世紀90年代萬邦烈等通過理論和試驗方法研究了螺桿-襯套副的嚙合理論與優化設計方法[4~6]。2000年以后許多學者進行了螺桿-襯套副的運動仿真和有限元計算,并取得了一定的成果[7~9],但對螺桿-襯套副運動學方面的研究僅限于對結構簡單的單頭普通內擺線型螺桿-襯套副螺桿在襯套內的運動軌跡和運動規律進行分析,針對螺桿-襯套副滑動速度的研究尚無報道,為此筆者對多頭短幅內擺線型螺桿-襯套副的線型設計、運動分析和滑動速度的計算方法進行系統的研究。
1 螺桿-襯套副的線型設計
螺桿-襯套副的空間共軛問題可轉化為平面共軛曲線副的相對運動問題[10],因此對螺桿-襯套副的嚙合狀況和運動分析可集中在其橫截面上。螺桿和襯套的橫截面曲線簡稱線型或型線。短幅內擺線型螺桿-襯套副的線型設計首先形成一條短幅內擺線作為襯套骨線,再利用外滾法形成螺桿骨線,最后分別向外側取骨線的等距線,形成螺桿-襯套副的線型。
首先采用無包心法形成Nw頭的短幅內擺線作為襯套骨線R(θ),其復矢量方程為[10]:
R(θ)=R2(Nejθ+Ke-jNθ)
(1)
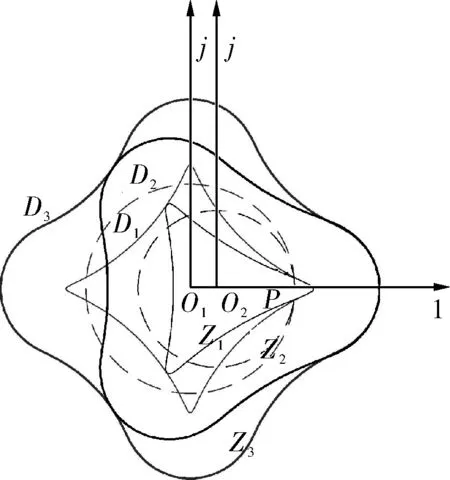
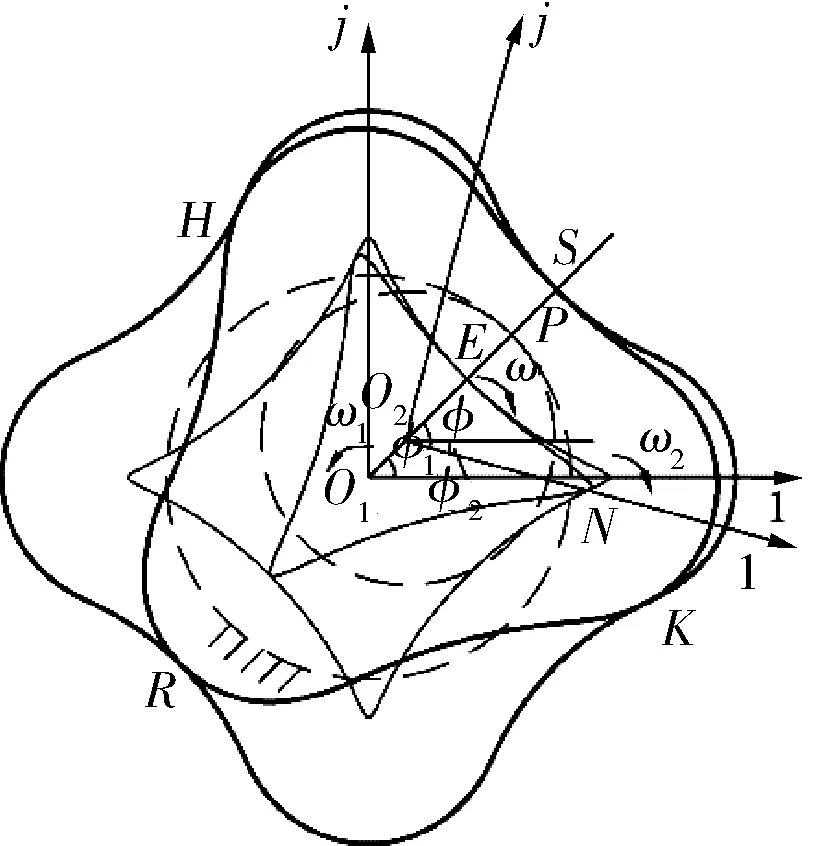
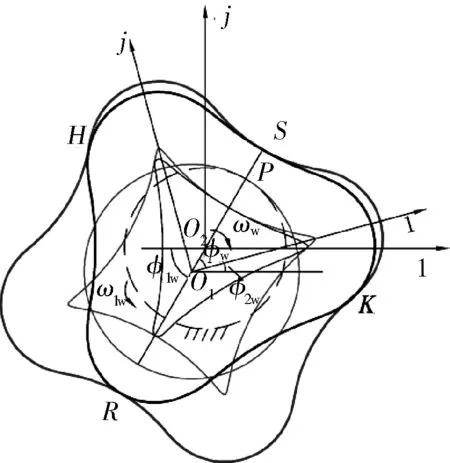
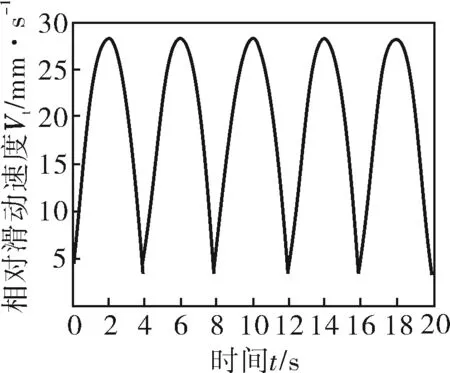
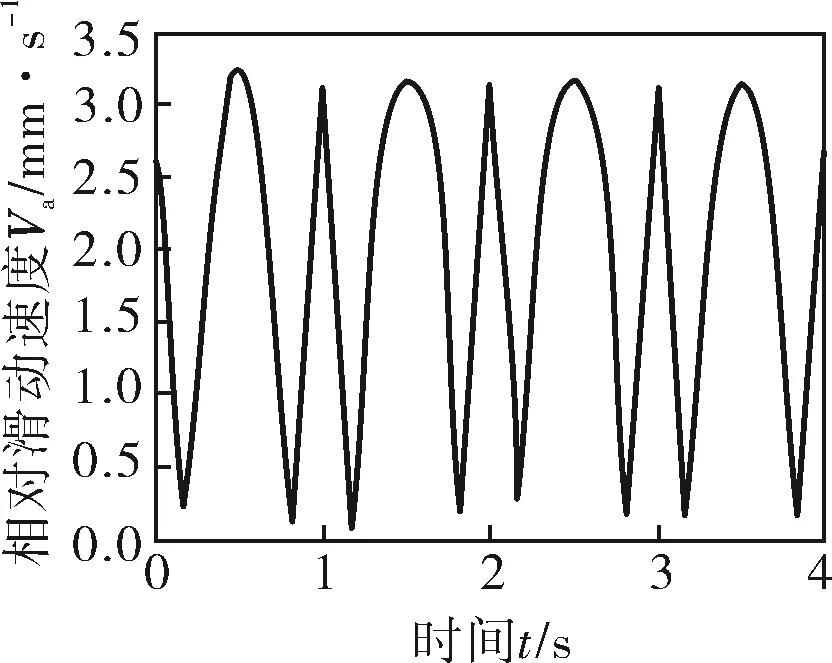
式中K——變幅系數,0 N——螺桿頭數,N=Nw-1; R2——滾圓半徑,mm; θ——導圓滾角,0≤θ≤2π。 形成短幅內擺線的導圓半徑R1與滾圓半徑R2的關系為: R1=NwR2 (2) 再采用外滾法,即以R(θ)的包心法導圓做動瞬心圓,攜帶R(θ)沿定瞬心圓外側做純滾動,R(θ)運動軌跡的內包絡線即為螺桿骨線,如圖1所示,其中動瞬心圓半徑R″與定瞬心圓半徑R′分別為: R″=NwKR2 (3) R′=NKR2 (4) 圖1 外滾法形成螺桿骨線 因此動瞬心圓與定瞬心圓的偏心距E(即螺桿-襯套副的偏心距)為: E=R″-R′=KR2 (5) 綜上,只要給定短幅內擺線型螺桿-襯套副的基本結構參數,即螺桿頭數N、偏心距E和變幅系數K,就可確定螺桿-襯套副的骨線,并滿足共軛條件。再給出等距半徑或等距半徑系數,則可設計出螺桿-襯套副的線型。 螺桿-襯套副的結構參數為:短幅內擺線型,變幅系數K=0.8,偏心距E=5mm,螺桿頭數N=3,等距半徑系數r0=2。根據上述線型設計方法得出螺桿-襯套副的線型如圖2所示。圖中曲線Z1、Z2、Z3分別表示螺桿的骨線、定瞬心圓和線型,曲線D1、D2、D3分別表示襯套的骨線、動瞬心圓和線型。為方便分析,在圖2中建立兩個復平面參考坐標系,其中1-O1-j的原點位于襯套型線的幾何中心,且與襯套固連,為靜坐標系;1-O2-j的原點位于螺桿型線的幾何中心上,且與螺桿固連,為動坐標系。 圖2 螺桿-襯套副嚙合的初始狀態 單螺桿式水力機械工作時一般螺桿旋轉,襯套不動,即定瞬心圓攜帶螺桿骨線和型線在動瞬心圓內做純滾動,稱為第一種嚙合運動,它可分解為兩種運動(圖3): a. 螺桿中心O2繞襯套中心O1做半徑為E的公轉,公轉角為φ1,公轉角速度為ω1,方向逆時針,螺桿的滾角為φ,滾角速度為ω,方向順時針,公轉角與滾角的關系為φ1=-Nφ/(N+1); b. 螺桿繞自身中心O2做自轉,自轉角φ2為公轉角與滾角的代數和,自轉角速度為ω2,方向為順時針,即φ2=φ/(N+1)。 圖3 第一種嚙合運動時間t時的嚙合狀態 螺桿-襯套副在嚙合過程中,螺桿骨線上的3個尖點將依次連續地劃過襯套骨線,這3個接觸點相對于螺桿來說是固定的,稱為固定接觸點(如點N);螺桿與襯套骨線間還有一個接觸點(E點),它沿襯套邊界逆時針流動,稱為流動接觸點。與螺桿骨線尖點對應的一段型線(圓弧),即螺桿的齒凸,其上的各點將依次與襯套型線接觸,因此對于型線來說,不存在固定接觸點,但流動接觸點仍然存在。為敘述問題方便,將型線的這兩類接觸點稱為螺桿齒凸接觸點(H、K、R點)和螺桿齒凹接觸點(S點),簡稱為齒凸接觸點和齒凹接觸點。 當φ>0的瞬時,螺桿齒凸與襯套齒凹由線接觸變為點接觸,螺桿的速度瞬心P沿定瞬心圓逆時針移動,而齒凸接觸點K(還有H、R)沿襯套輪廓順時針移動,齒凹接觸點S沿襯套輪廓逆時針移動;φ由0增大到π的過程中,瞬心到齒凸接觸點的距離PK逐漸增大到最大值;φ由π增大到2π的過程中,PK逐漸減小,直到螺桿齒凸又一次與襯套的下一個齒凹變為線接觸,完成螺桿與襯套嚙合的一個周期。由此可見,螺桿和襯套要完成一個循環的嚙合,螺桿導圓的滾角應為(N+1)2π。 3.1齒凸接觸點的滑動速度 外滾法形成螺桿-襯套副時相當于螺桿不動,襯套做行星運動,稱為第二種嚙合運動,它可分解為兩種運動(圖4): a. 襯套中心O1繞螺桿中心O2做半徑為E的公轉,公轉角φ1w,公轉角速度ω1w,方向為逆時針,襯套的滾角φw,滾角速度為ωw,方向為順時針,襯套的公轉角與滾角的關系為φ1w=-Nwφ/(Nw-1); b. 襯套繞自身中心O1自轉,自轉角φ2w為公轉角與滾角的代數和,自轉角速度為ω2w,方向仍為逆時針,即φ2w=-φw/(Nw-1)。 圖4 第二種嚙合運動時間t時的嚙合狀態 單螺桿式水力機械一般是螺桿旋轉,襯套不動,因此為了方便利用短幅內擺線型理論推導螺桿-襯套副的滑動速度,則要推出兩種嚙合運動的參數關系。圖3、4表示的是利用兩種運動形式達到相同嚙合狀態,由嚙合原理不難得到關系式φw=-φ1,φ1w=-φ,φ2w=-φ2。 由圖3可知,齒凸接觸點(如K點)的相對滑動速度Vt的表達式為: Vt=PK×ω2 (6) 由幾何矢量關系得: PK=O1K-O1P (7) O1K=O1N+NK (8) 則: Vt=(O1N+NK-O1P)ω2 (9) 其中,O1N為固定接觸點N在靜坐標系1-O1-j中的運動軌跡,即定子骨線;NK為等距半徑矢量;O1P為襯套導圓半徑矢量。 θ角和滾角φ的關系由短幅內擺線型固定接觸點的φ函數確定,φ函數為[10]: φw=-Nθ+2Tπ,0<θ<2π,T=0,1,2,…,N-1 (10) φw與固定接觸點對應,若只考慮螺桿骨線第一個尖點的運動軌跡,令T=0,則: θ=-φw/N (11) 由此可知: θ=-φ/(N+1) (12) 固定接觸點的運動軌跡即為襯套骨線,方向順時針,則矢量方程為: R(θ)=R2(Ne-jθ+KejNθ) (13) 由此可知: (14) 等距半徑矢量NK為: (15) (16) P點是兩導圓做純滾動時的速度瞬心,因此: O1P=R2(N+1)Kejφ1 (17) 結合上式,可得: (18) 整理得齒凸接觸點的相對滑動速度為: (19) 式(19)中滾角φ為順時針方向,為了在分析問題時,給φ代入正值,將φ前加上負號,式(19)變形為: (20) 將K=1分別代入式(20)、(16),整理后可得到普通內擺線型螺桿-襯套副間齒凸接觸點的相對滑動速度為: (21) 3.2齒凹接觸點的滑動速度 螺桿-襯套副在嚙合過程中,齒凹接觸點只有一個(S點),如圖3所示。該點的滑動速度Va表示為: Va=PS×ω2 (22) 由幾何矢量關系得: PS=O1E+ES-O1P (23) 其中,O1E為螺桿骨線流動接觸點在靜坐標系1-O1-j中的運動軌跡;ES為等距半徑矢量。 螺桿骨線流動接觸點的運動軌跡即襯套骨線,方向逆時針,則有: (24) 等距半徑矢量: ES=R2r0ejα=rejα (25) (26) 其中,α表達式前的正負號依據具體情況而定,應遵循等距向量朝外的原則。 θ和滾角φ的關系由短幅內擺線型流動接觸點的φ函數確定,φ函數為[10]: φw=-Nθ+2β+2Tπ,0≤θ<2π,T=0,1,2,…,N-1 (27) (28) 整理式(27)、(28),并取T=0(只分析第一頭)得: Nφ/(N+1)=-Nθ+2β (29) (30) 由此可見,θ與φ之間無法用初等函數來表達,只能利用數值分析方法,繪制φ曲線接觸圖,進而分析確定θ與φ的數值關系。 將式(18)、(24)、(25)分別代入式(22)、(23)得齒凹接觸點的滑動速度為: (31) 式中的α和θ由式(26)、(29)、(30)確定,都用滾角φ表達。 將K=1代入式(26)、(30)并利用三角函數變換,得: α=±(π/2)-(N-1)θ/2 (32) β=(N+1)θ/2 (33) 將式(33)代入式(29)得φ與θ的關系為: θ=-Nφ/(N+1) (34) 將式(32)、(34)代入式(31)得到普通內擺線型螺桿-襯套副齒凹接觸點的滑動速度為: (35) φ角為順時針,為了在分析問題時,給φ代入正值,則在φ前加上負號,則公式(35)變形為: (36) 4頭普通內擺線型螺桿-襯套副,設其偏心距E=10mm,等距半徑系數r0=1,自轉角速度ω2=π/10rad·s-1,滾角速度ω=π/2rad·s-1,公轉角速度ω1=2π/5rad·s-1。將數據分別代入式(21)、(36),并將滾角φ用時間t表示(φ=ωt)得: (37) (38) 利用MATLAB軟件將式(37)、(38)生成曲線如圖5、6所示。 圖5 齒凸接觸點的滑動速度曲線 圖6 齒凹接觸點的滑動速度曲線 由曲線可知,齒凸接觸點的滑動速度在襯套內凹處最小,在襯套內凸中點處最大;齒凹接觸點的滑動速度在離開襯套內凹處的瞬間最大,在襯套內凸中點最小;齒凹接觸點的滑動速度的最大值是齒凸接觸點的滑動速度的最小值;齒凸接觸點的嚙合周期是齒凹接觸點的N倍。 5.1單螺桿式水力機械中螺桿-襯套副的線型形成原理和過程較復雜,所涉及到的參數較多,分析確定了形成短幅內擺線型螺桿-襯套副線型所需的基本參數。 5.2分析了螺桿-襯套副的嚙合過程與規律,定義了螺桿-襯套副骨線間的固定接觸點和流動接觸點,以及螺桿-襯套副型線間的齒凸接觸點和齒凹接觸點。 5.3推導出了短幅(普通)內擺線型螺桿-襯套副齒凸接觸點和齒凹接觸點的相對滑動速度公式,并通過具體應用得出了螺桿-襯套副在嚙合過程中齒凸接觸點和齒凹接觸點滑動速度的變化規律。 [1] 蘇義腦,謝竹莊.螺桿鉆具馬達線型分析基礎及研究方法[J].石油鉆采機械,1985,13(6):10~20. [2] 蘇義腦,于炳忠,謝竹莊.單螺桿鉆具馬達線型分析[J].石油學報,1986,7(4):95~109. [3] 蘇義腦,謝竹莊.單螺桿鉆具馬達短幅內擺線等距線型分析[J]. 石油機械,1987,15(6):5~11. [4] 萬邦烈,曹玉德.短幅內擺線型單螺桿式水力機械螺桿- 襯套副的評價指標及參數的優選[J].石油礦場機械,1989,18(2):17~27. [5] 葛占玉,萬邦烈.單頭單螺桿式水力機械螺桿- 襯套副的嚙合理論及其作用力[J].中國石油大學學報,1990,14(5):33~40. [6] 劉孟,萬邦烈.單螺桿油氣混輸泵螺桿- 襯套副結構參數的優選[J].中國石油大學學報(自然科學版),1991,15(2):53~66. [7] 安永生,宋揚,張德實,等.螺桿泵轉子三維運動仿真分析及線型優化設計[J]. 中國石油大學學報(自然科學版),2012,36(3):155~164. [8] 郭爽,付保軍,劉建群.內擺線型單螺桿泵共軛副等距曲線運動分析[J].哈爾濱師范大學自然科學學報,2009,25(5):78~80. [9] 李曉明.單螺桿泵轉子在定子襯套中運動接觸跡的研究[J].機械工程及自動化,2007,143(4):58~60. [10] 蘇義腦.螺桿鉆具研究及應用[M].北京:石油工業出版社,2001:43~52,94~101.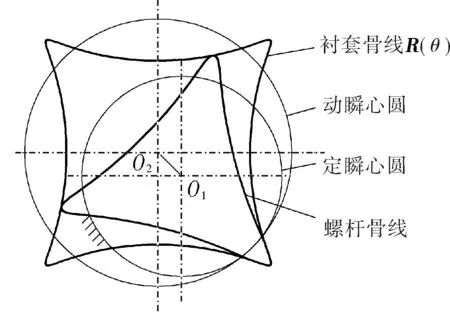
2 螺桿-襯套副的運動分析
3 螺桿-襯套副滑動速度的計算方法
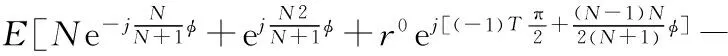
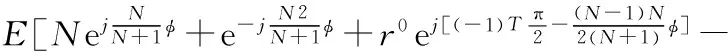
4 滑動速度計算公式的應用
5 結論

