妙思巧解，演繹數(shù)學(xué)魅力

朱延春

培養(yǎng)學(xué)生運(yùn)用數(shù)學(xué)知識解決實(shí)際問題的能力，是數(shù)學(xué)教學(xué)的目標(biāo)之一。現(xiàn)結(jié)合“巧妙解題”的教學(xué)實(shí)錄，介紹一下我是如何在解決問題的過程中，加強(qiáng)思維策略的指導(dǎo)，提升學(xué)生解決問題的策略水平的。

一、猜想——驗(yàn)證

自然科學(xué)，特別是數(shù)學(xué)中的新發(fā)現(xiàn)大都是從猜想開始的，這些猜想經(jīng)過大量的時(shí)間檢驗(yàn)，再經(jīng)過嚴(yán)密的論證推理，才獲得最終的定理、定論。在數(shù)學(xué)研究里，先猜想后證明，幾乎是一條規(guī)律。教師在組織教學(xué)時(shí)，要考慮如何創(chuàng)設(shè)情境，為學(xué)生再發(fā)現(xiàn)創(chuàng)造必要條件。

【例1】小白兔非常愛吃青菜，兔媽媽決定在它們家門前的空地上用籬笆圍一塊長方形菜地，自己種菜。要想種的青菜多，圍成的菜地面積就要盡量大，但自家籬笆的長度只有28米，菜地的長和寬各等于多少時(shí)，面積才能最大呢？

1.猜想——激活靈感

師：同學(xué)們，你有辦法使圍成的菜地面積最大嗎？

生1：若長方形的長為a米，寬為b米，周長是2a+2b=28米，那么長與寬的和就是a+b=14米，長方形的面積公式是“長×寬”，我們只要求出a×b的最大積就行了。

生2：因?yàn)檎叫问翘厥獾拈L方形，我們可以直接猜想“當(dāng)a=b時(shí)，也就是a=b=7。a×b取得最大值”。

生3：假設(shè)a×b的最大值為7×7=49，那么長方形的最大面積為49平方米。

2.驗(yàn)證——得出結(jié)論

師：大家的猜想非常有道理，但究竟對不對呢？拿出紙和筆來檢驗(yàn)一下，怎么樣？

同桌交流：把長方形的長和寬變化時(shí)面積的變化情況用表格的形式表示出來：

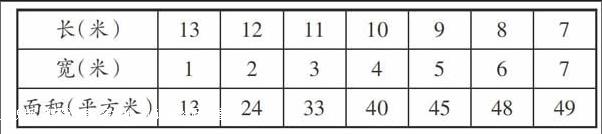
長方形邊長與面積變化規(guī)律表

[長（米）＼&13＼&12＼&11＼&10＼&9＼&8＼&7＼&寬（米）＼&1＼&2＼&3＼&4＼&5＼&6＼&7＼&面積（平方米）＼&13＼&24＼&33＼&40＼&45＼&48＼&49＼&]

生：耶！我們的猜想是正確的。

在教學(xué)中，教師要讓學(xué)生在“猜想——驗(yàn)證”活動中感受、領(lǐng)悟、理解和掌握數(shù)學(xué)的思想方法，培養(yǎng)學(xué)生勤于思考、勇于提出猜想，并對猜想進(jìn)行檢驗(yàn)的學(xué)習(xí)態(tài)度，形成獨(dú)特的個(gè)人見解，產(chǎn)生創(chuàng)新靈感。

二、探究——?dú)w納

【例2】把、、、化成小數(shù)（除不盡的保留三位小數(shù)）。

學(xué)生順利地把這些分?jǐn)?shù)化為小數(shù)后，頗有大功告成之態(tài)。見時(shí)機(jī)成熟，我故意說：“同樣是分?jǐn)?shù)，為什么有的能化成有限小數(shù)，而有的卻不能呢？”一石激起千重浪，學(xué)生在新問題面前個(gè)個(gè)凝神思索。這時(shí)，我啟發(fā)學(xué)生仔細(xì)觀察這幾個(gè)分?jǐn)?shù)有什么相同的地方。學(xué)生發(fā)現(xiàn)它們的分子都是7，我說：“對呀！為什么分子相同的有的能化成有限小數(shù)，而有的卻不能呢？”把學(xué)生的思考引到對分母的觀察與思考中去。他們終于發(fā)現(xiàn)：一個(gè)分?jǐn)?shù)能否化成有限小數(shù)，跟它們的分母有關(guān)，與它們的分子無關(guān)。接著請學(xué)生將這些分?jǐn)?shù)按照能否化成有限小數(shù)分成兩類，比較它們的分母有什么不同。引導(dǎo)學(xué)生初步歸納出：一個(gè)分?jǐn)?shù)，如果分母中除了2和5以外，不含有其他的質(zhì)因數(shù)，這個(gè)分?jǐn)?shù)就能化成有限小數(shù)，如果分母中含有2和5以外的質(zhì)因數(shù)，這個(gè)分?jǐn)?shù)就不能化成有限小數(shù)。

在課堂上，使學(xué)生主動地投入到知識的發(fā)生、形成、發(fā)展、運(yùn)用的過程中去，切實(shí)把他們推向思考問題的最前沿，這是課堂教學(xué)中激活學(xué)生思維的重要途徑。

三、數(shù)形——結(jié)合

“數(shù)”和“形”是數(shù)學(xué)中最基本的兩大概念。在教學(xué)中，要有目的地幫助學(xué)生把抽象的概念、復(fù)雜的數(shù)量關(guān)系與幾何圖形聯(lián)系起來考慮，為發(fā)展學(xué)生的直覺思維創(chuàng)造條件，能使題意形象具體，一目了然，從而較快地找到解題的途徑。

【例3】王大伯今年收獲了2.4噸蘋果，其中一半以上達(dá)到一級質(zhì)量標(biāo)準(zhǔn)，其余達(dá)到二級質(zhì)量標(biāo)準(zhǔn)。如果分等級出售，一級蘋果每千克為2.4元，二級蘋果每千克為1.6元;如果不分等級出售，每千克為1.8元。請你用計(jì)算器算一算，怎樣出售比較合適？

解：根據(jù)題意畫長方形示意圖。

[A][C][B][D][F][E][G][J][L][H] [2.4][1.8][1.6]

從長方形圖可見：不分等級出售，總收入為長方形ABCD的面積值。分等級出售，總收入為長方形AEFG和長方形EBJL面積和的值。需要比較長方形DHFG與長方形JLHC面積的大小，由于FH>HL，DH>HC，所以SDHFG>SJLHC。所以，分等級出售總收入更多，分等級出售更合算。

數(shù)學(xué)的思想方法是數(shù)學(xué)學(xué)科的精髓。日本著名數(shù)學(xué)家米山國藏認(rèn)為：作為知識的數(shù)學(xué)出校門不到兩年可能就忘了，唯有深深銘記在頭腦中的數(shù)學(xué)精神、數(shù)學(xué)的思想、研究方法和著眼點(diǎn)等，這些隨時(shí)隨地發(fā)生作用，使他們受益終身。”在課堂教學(xué)中，教師要積極而又審時(shí)度勢地把學(xué)生引向他們的“最近發(fā)展區(qū)”，給學(xué)生充分的獨(dú)立自主學(xué)習(xí)和探究操作的活動空間，讓學(xué)生在主動參與探究的過程中激活創(chuàng)新思維。

（責(zé)編 金 鈴）endprint