基于APDL參數化設計的艦船控制柜模態分析

程林風，王 驍

(中國船舶重工集團公司 第七一〇研究所，中國 宜昌 443003)

0 引言

在國防工業上，艦載電子設備是海軍各大作戰系統中必不可少的控制設備，在實戰環境中，武器之間的對抗會產生強烈的振動和沖擊，這些由沖擊振動產生的作用力對艦船控制設備的危害非常大。如果艦載電子設備的抗沖擊能力不足，就可能會因控制設備發生故障而使武器作戰系統無法發揮其作戰性能。因此，為了保證艦載武器系統工作可靠性，必須采取相應的防護措施。而實船試驗費用較高，并且可能會對艦載電子設備造成破壞性損壞。因此，在艦載電子設備的設計階段，就應通過計算機仿真手段來充分論證電子設備工作的可靠性，分析電子設備的動力特性和響應［1-2］。

1 艦船控制柜的APDL參數化建模

以某型艦船控制柜為例，本文對艦船控制柜進行參數化有限元建模，圖1是本文研究對象的三維實體模型。

圖1 艦載電子機柜三維實體模型分解圖

該型艦載電子機柜的外形尺寸如表1。

表1 艦載電子機柜柜體尺寸

該型艦船控制柜內部4個分機的結構尺寸及重量如表2。

表2 各分機尺寸及重量

該型艦船控制柜內部有4個分機，從下至上依次編號分機1、分機2、分機3、分機4，其中分機1、分機2和分機3結構類似，都是梁支撐面板的結構。，并通過導軌安裝在柜體內部，分機4兩側通過螺釘與柜體固定。柜體內的橫梁通過螺釘固定在柜體的側壁。底座和后背通過復合阻尼隔振器固定在船艙內。

利用APDL參數化設計語言建立樣機的有限元參數化模型，命令流如下:

得到的參數化有限元模型如圖2。

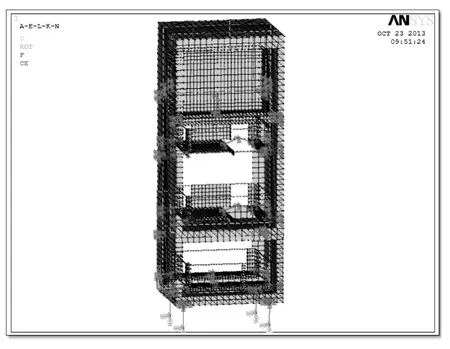
圖2 艦載電子機柜的有限元模型

圖 2 為運用 SHELL63，BEAM188，MASS21 和COMBIN14單元［3-4］建立的艦船控制柜整體機柜的有限元模型。

2 模態分析的理論基礎［5-7］

任何振動系統的力學模型都是由三種理想化的元件組成，它們是:質量塊、阻尼器和彈簧。因此任何一個復雜的系統都可以用如下力學方程表示:

其中:[M]:結構質量矩陣;

[C]:結構阻尼矩陣;

[K]:結構剛度矩陣;

{F( t)}:隨時間變化的載荷函數;

{u}:節點位移矢量;

{u'}:節點速度矢量;

{u″}:節點加速度矢量。

一個多自由度無阻尼自由振動系統，其運動微分方程為:

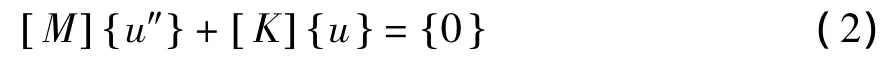
方程(2)可簡化為:

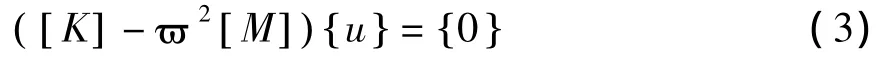
這是一個關于{u}的n元線性齊次代數方程組，該方程組有非零解的充要條件是它的系數行列式等于零，即:

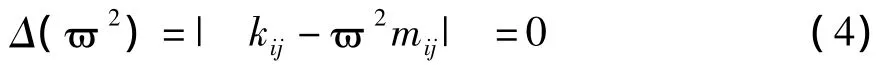
式(4)稱為系統頻率方程，該行列式稱為特征行列式。將它展開后可得到關于?2的n次代數方程:

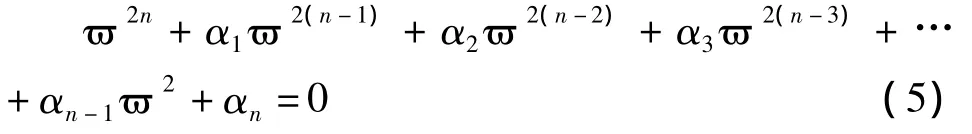
假定系統的質量矩陣與剛度矩陣都是正定的實對稱矩陣。在數學上可以證明，在這一條件下，頻率方程(5)的n個根均為正實根，它們對應于系統的n個自然頻率，這里假設互不相等，即沒有重根，因而可以由小到大按次序排列為:

式(6)中最低頻率?1稱為基頻，在工程應用中它是最重要的一個自然頻率。

將各特征值λr=?r2分別代入式(3)可得各相應的解{u(r)}，稱為系統的模態向量或振型向量。

3 艦船控制柜模態分析

3.1 柜體的模態分析

柜體是重要的支撐設備，其自身剛度的好壞直接決定了內部分機和各電子元器件的動態性能，因此，有必要對其進行模態分析。

在ANSYS中，完全自由狀態下的模態分析的前6階模態視為模型的剛性移動，前6階模態的固有頻率都接近0 Hz，因此，從第7階模態開始才是系統自由振動下的第1階固有頻率，通過模態分析并提取結果如表3。

表3 柜體自由振動下固有頻率及振動形式

柜體自由振動狀態下的振型如圖3至圖4。

圖3 柜體第1階固有振型

圖4 柜體第2階固有振型

由柜體前5階固有頻率和固有振型可以看出，柜體的第1階固有頻率為60.5 Hz，固有振型表現為整體扭曲，而后4階固有振型主要表現在上側壁面的彎曲振動。根據柜體的結構特點可知，由于中間橫板的作用，下側壁面在振動中振幅較小，而上側壁面振動較劇烈，如果受到頻率相近的外部激勵，上側壁面將是柜體的薄弱環節。

3.2 兩類分機的模態分析

電子機柜的分機從結構特征上可以分為兩類，分別為橫梁結構形式和薄板拼焊結構形式。對兩類分機進行模態分析得到其第1階固有頻率和振動形式如表4。

表4 兩類分機自由振動下第1階固有頻率及振動形式

第1階固有振型如圖5至圖6。

圖5 橫梁支撐形式分機第1階固有振型

圖6 薄板拼焊形式分機第1階固有振型

根據結構之間的倍頻規則［7-8］，機柜的第1階固有頻率至少要小于分機頻率的一半，或小于其兩倍，使框架和分機之間不發生耦合振動，以免放大傳遞到分機及其上面的元器件上，加速失效的進程。

基于這個原則，橫梁支撐形式分機的第1階固有頻率為126.3 Hz，柜體的第1階固有頻率為60.5 Hz，大于60.5 Hz的兩倍，橫梁支撐形式的分機結構設計合理。薄板拼焊結構形式分機的第1階固有頻率為21.2 Hz，遠小于柜體的第1階固有頻率60.5 Hz，不滿足倍頻原則。在整體機柜中，頂上分機的存在對整體機柜的動態性能也會產生重大影響。因此，必須對頂上分機結構進行加固，使其滿足設計要求。

3.3 艦船控制柜整體機柜的模態分析

考慮到兩類分機的不同影響以及分機內電子元器件對整體機柜固有特性的影響，本文分別對艦船控制柜以下三種情況進行分析。

3.3.1 電子機柜中含有帶橫梁支撐形式的分機模態分析

這種狀態下艦船控制柜的固有頻率和固有振型如表5。

表5 含前3個分機時自由振動下固有頻率及振動形式

固有振型如圖7至圖8。

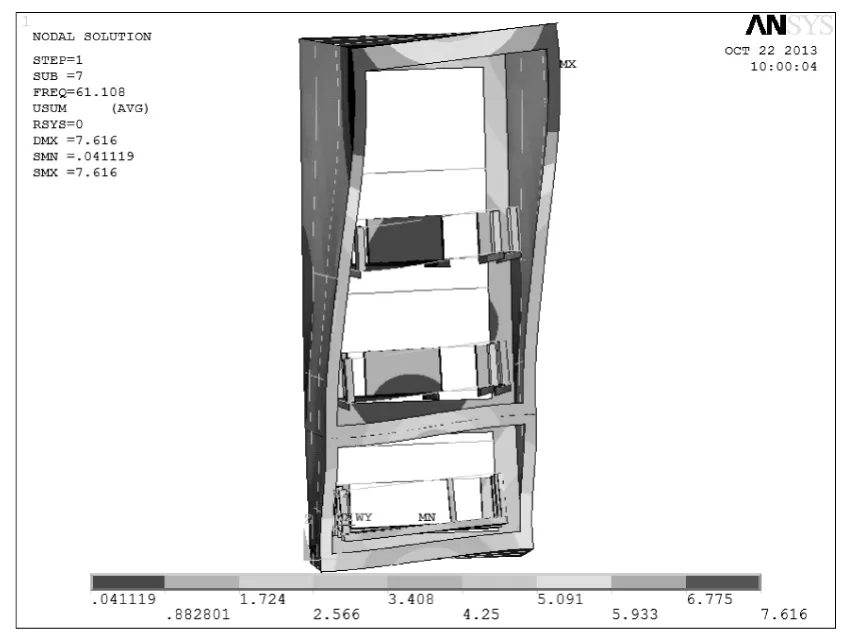
圖7 含三個分機的第1階固有振型

圖8 含三個分機的第2階固有振型

3.3.2 含四個分機(不含電子元器件的質量)的艦船控制柜模態分析

這種狀態下艦船控制柜的固有頻率和固有振型如表6。

表6 含4個分機時自由振動下固有頻率及振動形式

固有振型如圖9至圖10。

圖9 含四個分機的第1階固有振型

3.3.3 含四個分機(含電子元器件的質量)的艦船控制柜模態分析

圖10 含四個分機的第2階固有振型

這種狀態下艦船控制柜的固有頻率和固有振型如表7。

表7 整體機柜含質量時自由振動下固有頻率及振動形式

固有振型如圖11至圖12。

圖11 含質量的第1階固有振型

圖12 含質量的第5階固有振型

4 結論

綜合前面模態分析的結果數據，四種狀態下的電子機柜模態分析結果統計如圖13。

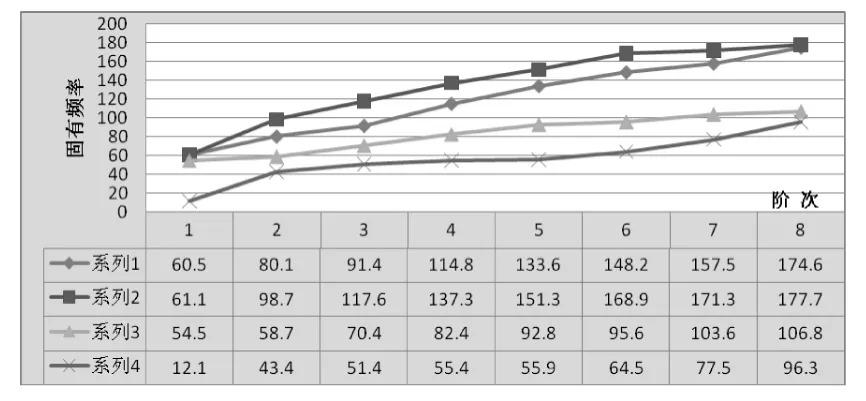
圖13 電子機柜不同狀態下的固有頻率擬合曲線

(注:系列1表示柜體的前8階固有頻率表曲線;系列2表示含前3個分機時的固有頻率曲線;系列3表示含4個分機不含元器件質量的固有頻率曲線;系列4表示含4個分機含電子元器件質量的固有頻率曲線。)

由圖13可得出如下結論:

1)從固有振型上看，在沒有安裝4號分機之前，機柜的第1階固有振型表現為整體扭曲，而安裝4號分機后，第1階模態表現為4號分機的振動。這是由于4號分機自身剛性較差造成的(4號分機第1階固有頻率為21.2 Hz)，因此，4號分機對艦載電子機柜的動態特性影響較大;

2)在增加各電子元器件質量后，由于質量的增加，而系統剛度未得到提升，因此整體機柜的固有頻率大幅下降，又由于整體機柜中4號分機自身剛度較差，且在四個分機中，它的質量相對較大(22 kg)，導致整體機柜的固有振型中4號分機的振動尤為突出，因此，可以推斷，質量對于整體機柜動態性能影響巨大，尤其是對于4號分機;

3)增加質量之后，艦船控制柜整體固有頻率下降，因此，質量對系統的影響不可忽視，而4個分機中1號分機較安全，是否可以在1號分機中分配更多的質量，因此，可以考慮四個分機如何分配質量，使得系統的動態性能最好;

4)結合艦船控制柜在不同狀態下對應整體扭曲的固有頻率，可以發現分別為60.5 Hz、61.1 Hz、58.7 Hz、64.5 Hz，說明了機柜的整體扭曲的固有頻率基本不變。

［1］ 生建友，王明月，等.電子設備機箱設計.電訊技術，2005

［2］ 張衛芬.電子機柜分機的結構優化設計.東南大學碩士學位論文，2006

［3］ 王新敏，李義強，許宏偉編著.ANSYS結構分析單元與應用［M］.北京:人民交通出版社，2011.9

［4］ 李響鑄.基于ANSYS軟件PDS模塊機械零件狀態函數靈敏度分析.吉林大學碩士論文，2006

［5］ 邱成悌，趙惇殳，等.電子設備結構設計原理［M］.南京:東南大學出版社，2001:132-133，523-525

［6］ 師漢民.機械振動系統——分析·測試·建模·對策.武漢:華中科技大學出版社，2004

［7］ 李朝旭.電子設備的抗振動設計［J］.電子機械工程，2002，18(1):51-53

［8］ Steinberg，Dave.S.Vibration analysis for electronic equipment［M］.2nd Ed.John Wiley and Sons:New York，1988:414-420