縮短艦載光電跟蹤儀調舷時間的研究
宋曉明,劉小強,壽少峻,柳井莉
(西安應用光學研究所 陜西 西安 710065)
艦載光電跟蹤儀作為對敵目標的一種探測設備,以其探測目標時跟蹤精度高、抗干擾能力強和作戰時可直接獲得目標的圖像等特點,在現役各種武器系統中大量裝備,在現代國防中受到越來越多的重視[1]。光電跟蹤儀調舷時間的縮短意味著武器系統反應時間的減小,給后續火控、武器攻擊爭取了先發的時間,相應提升了我方裝備、人員的戰場生存能力[2]。
1 研究課題提出
1.1 調舷簡介
光電跟蹤儀接收到以大地球坐標系表示的目標方位指示數據Bc及距離指示數據Rc后,根據光電跟蹤儀當前在大地球坐標系中所處的角位置B0,方位伺服系統自動以最快的時間從任意的當前位置B0用最佳運動方式靠向Bc位置,同時仰角伺服系統也從任意的當前位置E0快速運動到所需定位的位置Ec,完成調舷,以便對目標進行空域搜索、捕獲與跟蹤。
對動態系統來說,一個重要的指標就是完成給定任務所需的時間,特別對于光電跟蹤儀這種跟蹤系統來說,快速反應是它們的致命點,而大角度調舷時間占武器反應時間的一大部分,因此,如何快速調舷在工程上是個很有意義的課題[3]。
1.2 常用調舷速度曲線
目前常用的調舷速度曲線主要有以下3種:
1)直線型加減速速度曲線。此種加減速控制方法加減速過程快速,計算簡單,節省資源[4]。
2)指數型加減速速度曲線。此種方法符合系統固有頻率,加減速過程快速而平穩適用于控制系統處理速度快且對加減速過程要求高的場合[5]。
3)S型加減速曲線。其運動過程依次為加加速運動階段,加速運動階段,減加速運動階段,勻速運動階段,加減速運動階段,加減速運動階段,減速運動階段,減減速運動階段。主要適用于對加減速平穩性要求較高的場合[6]。
1.3 調舷速度曲線的選取
某艦載光電系統在初樣機設計中,采用的加減速曲線為:直線升速,指數曲線減速。在實驗中,我們發現,指數曲線減速收斂比較慢,調舷耗時較長,且計算量偏大,占用資源較大。
由于該光電系統跟蹤的目標為快速目標,對速度要求較高,并且控制計算機任務繁重,要求調舷占用盡量少的資源,因此,在改進中采用了直線型加減速曲線進行調舷。
一般情況下最佳快速調舷的速度曲線由最大加速度、最大恒速保持段和最大減速段三部分組成,呈等腰梯形。當調舷行程比較短時,沒有最大恒速保持段,因而呈等腰三角形。最佳快速調舷速度曲線采用等腰梯形模型,但實際編程時最好采用非等腰梯形模型,即速度上升段的加速度取得大一些,而速度下降段的加速度則取得小一些。這樣做主要是考慮到若速度下降段的加速度取得過大,容易使角度位置沖過頭,而不利于最終的位置鎖定。
2 實驗驗證
為驗證調舷改進設計的可行性,本研究以某型光電系統為硬件平臺,采用了直線型加減速曲線與現有的指數型加減速曲線對比,以調舷期望性能參數為指標規劃了調舷運動過程,最后在某型光電系統硬件平臺上進行調舷操作,并錄取數據,與現有系統調舷數據進行對比并對之進行評估。
2.1 調舷方式規劃及指標
通過某型光電系統平臺核算,其調舷可按如下方式及性能進行規劃:
1)方位機構
方位機構調舷時采用“不等腰梯形”模型進行調舷。
方位大角度調舷期望模型如下圖所示,方位最大調舷速度≥250°/s;速度上升段最大調舷加速度≥900°/s2,速度下降段最大調舷加速度≥700°/s2;

圖1 方位調舷速度理論上曲線模型(0°-90°)Fig.1 Azimuth Adjust side speed curve model on theory(0°-90°)
90°典型調舷速度曲線為一不等腰三角形,過程分為兩部分,加速段,減速段。可計算出:
加速段時間:t1=0.295 8 s;加速段行程:S1=39.38°。
減速段時間:t2=0.380 3 s;減速段行程:S2=50.62°。
0°—90°方位調舷時間為 t=t1+t2+0.676 s。
2)俯仰機構
俯仰機構調舷時采用“等腰梯形”模型進行。
俯仰大角度調舷期望模型如圖2所示,俯仰最大調舷速度≥200°/s;俯仰最大調舷加速度≥500°/s2;

圖2 俯仰調舷速度曲線模型(0°-85°)Fig.2 Elevation Adjust side speed curve model on theory(0°-85°)
85°典型調舷速度曲線為一等腰梯形,過程分為3部分,加速段,減速段,恒速段。可計算出:
加速段時間:t1=0.4;加速段行程:S1=40°。
恒速段時間:t2=0.025 s;恒速段行程:S2=5°。
減速段時間:t3=0.4 s;減速段行程:S3=40°。
0°—85°俯仰調舷時間為 t=t1+t2+t3+0.825 s。
2.2 實驗結果
經臺架測試,并通過操控系統記錄典型調轉過程的速度、位置數據,測試結果與改進前光電平臺調舷性能對比。
1)方位 90°調舷
現有系統以加速段以700°/s2加速度加速,減速段使用指數曲線收斂,最后閉位置環。位置曲線和速度曲線見下圖。

圖3 現有系統方位90°調舷位置曲線Fig.3 Azimuth90°Adjust side position curve

圖4 現有系統方位90°調舷速度曲線Fig.4 Azimuth90°Adjust side speed curve
改進后系統以加速段以900°/s2加速度加速,減速段以700°/s2加速度減速,最后閉位置環。位置曲線和速度曲線見下圖。

圖5 改進后系統方位90°調舷位置曲線Fig.5 Improved azimuth90°adjust side position curve

圖6 改進后系統方位90°調舷速度曲線Fig.6 Improved azimuth 90°djust side speed curve
2)俯仰 85°調舷
現有系統以加速段以336°/s2加速度加速,減速段使用指數曲線收斂,最后閉位置環。位置曲線和速度曲線見下圖。
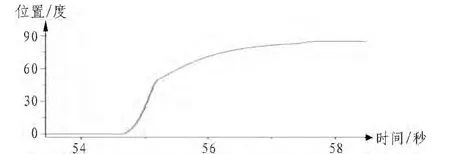
圖7 現有系統俯仰85°調舷位置曲線Fig.7 Elevation85°Adjust side position curve

圖8 現有系統俯仰85°調舷速度曲線Fig.8 Elevation85°Adjust side speed curve
改進后系統以加速段以500°/s2加速度加速,減速段以500°/s2加速度減速,最后閉位置環。位置曲線和速度曲線見下圖。

圖9 改進后系統俯仰85°調舷位置曲線Fig.9 Improved Elevation85°Adjust side position curve

圖10 改進后系統俯仰85°調舷速度曲線Fig.10 Improved Elevation85°Adjust side speed curve
通過上述曲線,系統改進前后速度、加速度和調舷時間等參數對比如下表。
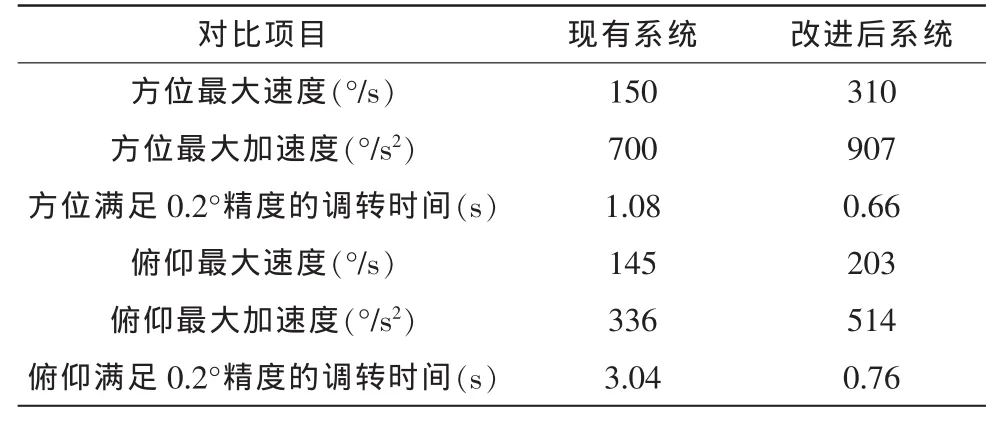
表1 系統改進前后參數對照表Tab.1 Pre-and post-parameter system improvements table
3 結束語
實驗證明,對比了目前系統的調舷性能和調舷改進后通過專題試驗測試的性能,從表1可以看出,改進設計可行,且改進后大大縮短了調舷時間,改進后方位90°典型調舷時間由原系統的1.08 s縮短到0.66 s,俯仰85°典型調舷時間由原系統的3.04 s縮短到0.76 s。由此可見選擇合理的調舷曲線,在保證調舷精度的前提下,可以有效縮短調舷時間。
[1]王小鵬,紀明.光電系統工程概念、設計與思考[J].應用光學,2007:1-6.WANGXiao-peng,JIMing.The concept, design and thinking of optical systems[J].Applied Optics,2007:1-6.
[2]楊超,張東泉.基于S曲線的步進電機加減速的控制[J].機電工程,2011(7):23-28.YANG Chao,ZHANG Dong-quan.Acceleration and deceleration of stepper motor control based on s-curve[J].Journal of Mechanical&Electrical Engineering,2011(7):23-28.
[3]李錫文,姜德美.步進電動機加速運行控制研究[J].微電機2007(10):35-42.LI Xi-wen,JIANGDe-mei.Control of stepper motor acceleration run[J].Micromotors,2007(10):35-42.
[4]劉威鑫,胡仕兵.用C51語言實現步進電機的運行速度控制[J]. 計算技術,2001(1):43-48.LIU Wei-xin,HU Shi-bing.speed control of stepper motor based on C51[J].Computing Technology,2001(1):43-48.
[5]劉穎,王志剛.步進電機升降頻的優化算法[J].工程自動化技術,2010(8):25-29.LIU Ying,WANG Zhi-gang.Optimization algorithm of stepper motor frequency[J].Engineering Automation Technology,2010(8):25-29.
[6]葉勇,蔣靜坪.開關磁阻的再生制動實現[J].中國電機工程學報2004(2):101-104.YE Yong,JIANG Jing-ping.Switched reluctance to achieve regenerative braking[J].Proceeding of the CSEE,2004(2):101-104.

