電梯曳引鋼絲繩力學分析及實驗研究*

尤光輝，張 憲，鐘 江，俞思源

(1.浙江省特種設備檢驗研究院，浙江杭州310020;2.浙江工業大學特種設備制造與先進加工技術教育部重點實驗室，浙江杭州310014;3.杭州應用聲學研究所，浙江杭州310012)

0 引言

隨著電梯曳引鋼絲繩廣泛使用，其斷絲斷股現象時有發生，由于鋼絲繩的原因引發的電梯事故也不時見諸媒體，電梯鋼絲繩的斷絲斷股等情況給使用單位和乘客帶來了極大的安全隱患，其質量和壽命引起了廣大學者關注。通過對電梯曳引鋼絲繩內部進行受力分析，給電梯曳引鋼絲繩設計單位來改善其性能依據，對提高全國電梯整體安全水平和保障人民群眾乘梯安全和經濟性有重要意義。國外學者Erdonmez 等［1］針對鋼絲繩復雜的幾何形狀，提出了用幾何方程來確定鋼絲繩芯的模型。Usabiaga 等［2］和E.Stanova 等［3］建立分別建立受力模型和數學幾何模型，并對其進行分析鋼絲繩損傷。王曉宇等［4］總結了鋼絲繩幾何特征及分析鋼絲繩在拉壓、彎曲和局部接觸等載荷的情況下非線性力學現象，對鋼絲繩結構和相關力學分析進行了探討。孫建芳［5］通過對鋼絲繩幾何模型的建立，對鋼絲繩力學強度及簡單直股、獨立繩芯進行了應力分析。劉玉輝等［6］和許波波等［7］提升繩進行研究，分析了其受力情況及對其壽命影響進行了探討。由于電梯曳引鋼絲繩的磨損直接影響電梯安全，對其進行力學分析十分必要。

本研究對電梯曳引鋼絲繩1 ×19 結構和8 ×19 結構進行力學研究。

1 電梯曳引鋼絲繩力學分析

1.1 單根鋼絲的受力分析

假定電梯曳引鋼絲繩股中芯絲直徑足夠大，根據同層鋼絲不接觸的理論判斷，同層鋼絲之間不接觸而只與芯絲接觸，同層鋼絲之間的摩擦力遠小于外部載荷，不考慮摩擦力影響。鋼絲變形前、后及載荷示意圖如圖1所示。

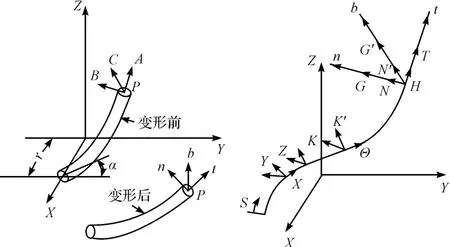
圖1 鋼絲變形前、后及載荷示意圖

根據Costello 的彈性理論［8］，筆者建立電梯曳引鋼絲繩的力學模型，單根鋼絲的受力情況如圖1所示，根據力學平衡知識可以得到下列平衡方程:

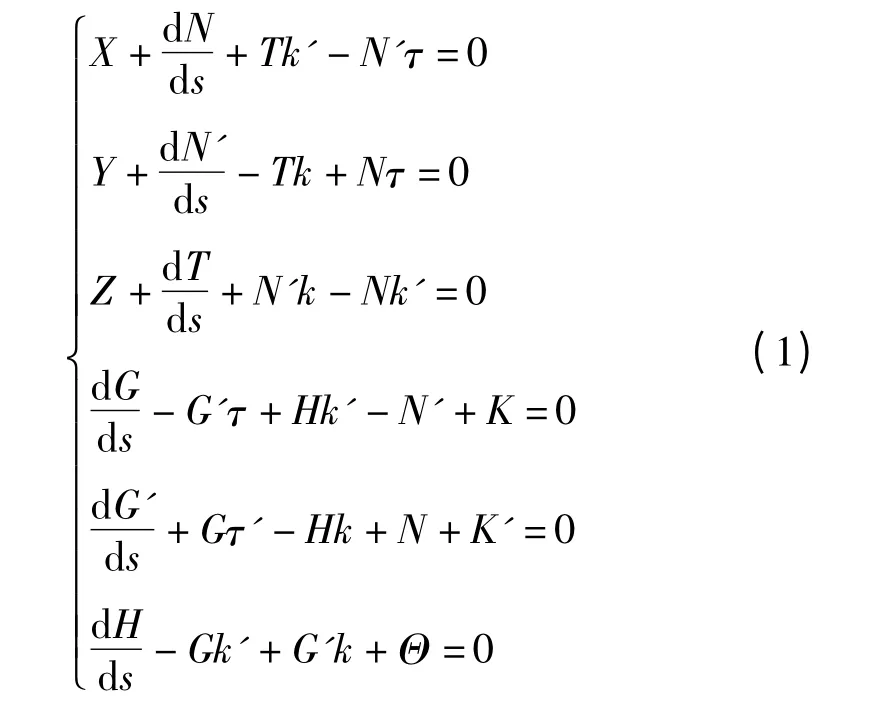
1.2 單股電梯曳引鋼絲繩的受力分析

單股電梯曳引鋼絲繩(1 ×19)結構由1 根芯層鋼絲，6 根內層鋼絲和12 根外層鋼絲組成，是以一定螺旋角相互纏繞在一起的。單股電梯鋼絲繩結構圖及受力圖如圖2所示。

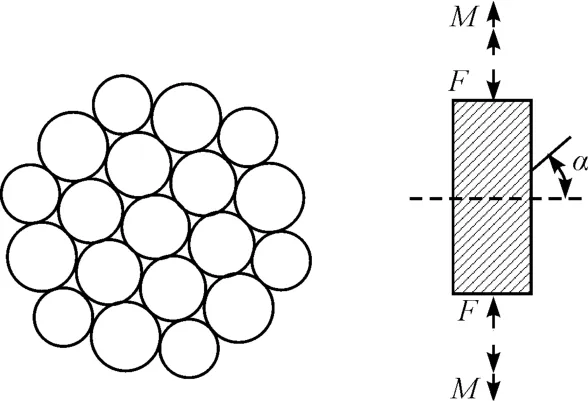
圖2 單股鋼絲結構及受力情況

單股中芯層、內層、外層的半徑分別為R0、R1、R2，F、M 分別為單股鋼絲繩所受的軸向力和軸向力矩，受力后鋼絲的螺旋結構發生改變，鋼絲在不受力狀態下以及受軸向力后的曲率和撓率分別為:

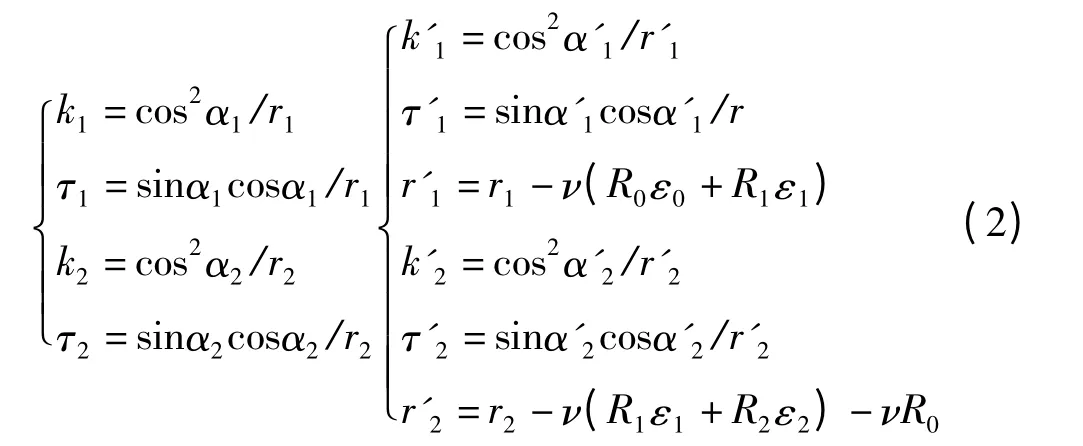
式中:α1，α2—內層和外層鋼絲的初始捻角;r1，r2—內層和外層鋼絲的螺旋半徑，k1，k'1—內層鋼絲變形前后的曲率;k2，k'2—外層鋼絲變形前后的曲率;τ1，τ'1—內層鋼絲變形前后的撓率;τ2，τ'2—外層鋼絲變形前后的撓率;α'1，α'2，r'1，r'2—內層、外層鋼絲變形后的捻距和螺旋半徑;ν—鋼絲的泊松比;ε0，ε1，ε2—芯層、內層、外層鋼絲的軸向應變(下標為0—鋼絲芯層，1—鋼絲內層，2—鋼絲外層，下同)。

假設單股電梯曳引鋼絲繩的側線鋼絲單位長度不受外部力矩，即k1=0 和k'1=0，而單股鋼絲所受的軸向力是常數，故dN=0。筆者認為芯層、內層和外層鋼絲泊松比均為ν，則由式(1)可得:

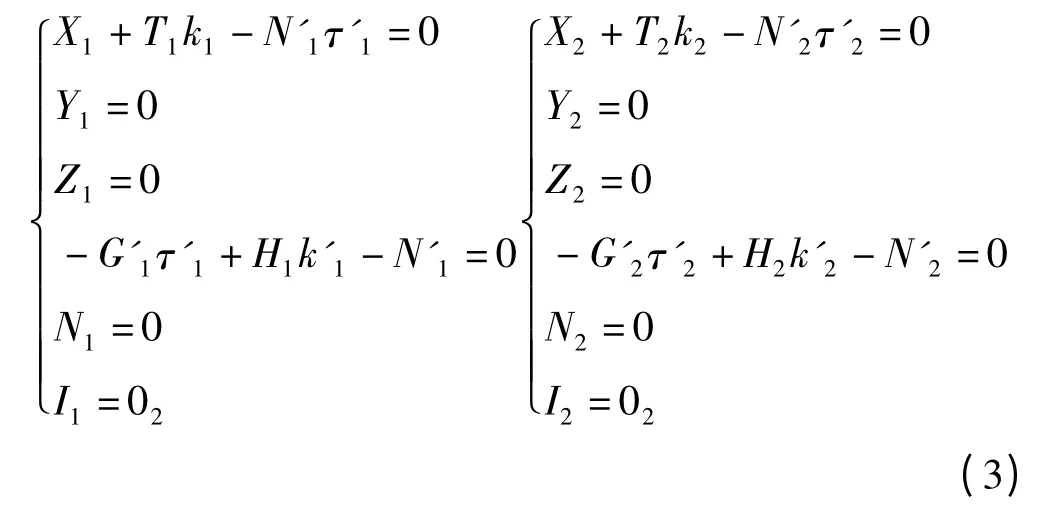
根據彈性力學知識，可得單股側線內層和外層鋼絲受力方程和力矩方程如下關系:

式中:Δk1，Δk2，Δτ1，Δτ2—內外層鋼絲變形前后曲率和撓度的變化;E—彈性模量;C—剪切模量。

根據圖2 和式(4)，可得單股側線內外層鋼絲的力及力矩平衡方程:

式中:F0，F1，F2，F總—單股鋼絲繩芯層、內層、外層及單股鋼絲繩的軸向力;M0，M1，M2，M總—單股鋼絲繩芯層、內層、外層鋼絲及單股鋼絲繩的軸向力矩;n1，n2—單股鋼絲繩內層、外層鋼絲的總數目;ψ—單位長度扭轉角。

螺旋股鋼絲繩的扭轉軸向力矩的公式為:

式中:M—鋼絲繩扭矩;C—常數，在此取0.82［9］;d—鋼絲繩直徑;F—鋼絲繩軸向力。

1.3 電梯曳引鋼絲繩的受力分析

本研究采用電梯常用的8 ×19 結構的鋼絲繩建立數學模型并進行力學分析。該類的電梯曳引鋼絲繩是8 個側股以一定的螺旋角纏繞在芯股上形成的。

為了便于電梯曳引鋼絲繩建立數學模型和力學分析，筆者將8 ×19 類結構電梯曳引鋼絲繩的每一股看成整體，芯股及側股分別等效看成芯層鋼絲和內層鋼絲，就等效為單股電梯曳引鋼絲繩的受力情況，由式(5)可得整根電梯曳引鋼絲繩的受力方程，有如下的關系:

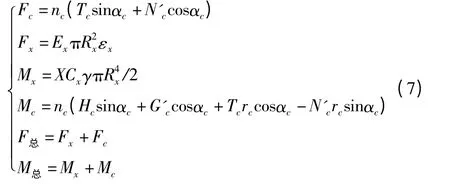
式中:下標x—芯股，c—側股;γ—鋼絲繩的旋轉應變，對于鋼芯X=1，對于麻芯，認為麻芯和鋼芯一樣承受載荷作用，取X=1，認為(麻芯)不承受載荷X =0。若是電梯曳引鋼絲繩的芯股為鋼芯層時，則νc=ν。鋼絲繩(麻芯)的彈性模量取麻芯的彈性模量和泊松比分別為Ex=0.08 ×105MPa，νx=0.4。

2 仿真結果分析

為研究各個鋼絲的受力及應力情況，筆者利用Matlab/Simulink 對8 ×19 結構，芯股為麻芯，直徑為10 mm，側股鋼絲捻距p =130 mm 的電梯曳引鋼絲繩受力過程進行編程建模，不考慮繩麻芯受力。

該模型的輸入變量為鋼絲繩的結構參數和受力值，輸出結果為各個鋼絲的軸向應力和接觸應力值。在計算過程中使用的參數如表1所示。

表1 電梯曳引鋼絲繩結構參數

在Simulink 仿真計算中，將鋼絲應變計算程序以s函數的形式［10］封裝在模塊中。鋼絲繩受力分析的Simulink 仿真模型如圖3、圖4所示。

圖3 電梯曳引鋼絲繩受力模型

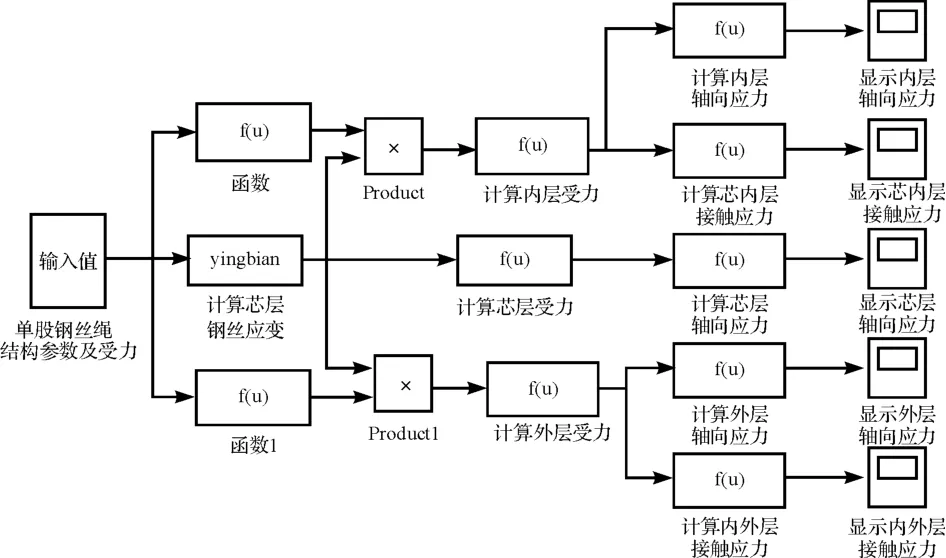
圖4 單股電梯曳引鋼絲繩受力模型

2.1 單股電梯曳引鋼絲繩應力

根據電梯曳引鋼絲繩的受力模型，得到結果如表2、表3所示。

表2 單股(側股)電梯曳引鋼絲繩計算結果

表3 電梯曳引鋼絲繩計算結果

由表2 可知，對于側股電梯曳引鋼絲繩來說，芯層鋼絲的軸向力最大，其次是內層鋼絲的軸向力，外層鋼絲繩的軸向力最小。對于接觸應力來說芯層與內層鋼絲的接觸應力要大于內層與外層之間的鋼絲，所以單股電梯曳引鋼絲繩中，芯層鋼絲應力集中，也最容易發生磨損，最易失效。其余股(芯股和側股)各個鋼絲軸向力、接觸應力的規律與該股鋼絲是一致的。

2.2 整根電梯曳引鋼絲繩應力

從表2 和表3 的計算結果可知，對整根電梯曳引鋼絲繩來說，接觸應力大小的順序:芯股與側股之間最大，股內芯層與內層之間次之，股內內層與外層之間的最小，發現電梯曳引鋼絲繩股與股之間的鋼絲磨損最為嚴重。

2.3 不同的芯層半徑對接觸應力的影響

本研究對受軸向力4 500 N，內層和外層鋼絲半徑分別為0.6 mm、0.5 mm，芯層鋼絲半徑為0.7 mm ～1.4 mm的單股鋼絲繩進行分析，得到的結果如圖5所示，兩條曲線分別為芯層—內層及內層—外層鋼絲的接觸應力情況隨芯層鋼絲半徑變化的情況。

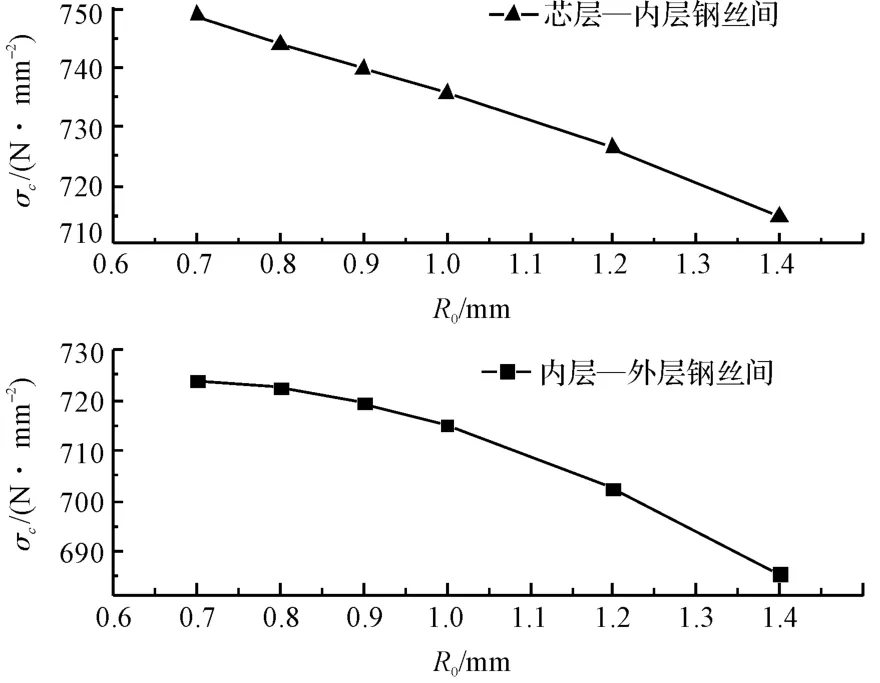
圖5 芯層鋼絲半徑對接觸應力的影響

當芯層鋼絲半徑從0.7 mm 變到1.4 mm，從圖5可知芯層鋼絲與內層鋼絲、內層鋼絲與外層鋼絲的接觸應力隨芯層鋼絲半徑增大而減少。

因此，在設計電梯曳引鋼絲繩時采用的芯層鋼絲半徑比側線鋼絲的半徑要大，這可改善內部應力的分布，增強其強度和大大延長其壽命，也可防止在磨損過程中由于芯層鋼絲半徑變小而引起破壞。

2.4 不同的內層半徑分析對接觸應力的影響

本研究對受軸向力4 500 N，芯層和外層鋼絲半徑分別為0.8 mm、0.5 mm，內層鋼絲半徑為0.4 mm ～0.75 mm的單股鋼絲繩進行分析，得到的結果如圖6所示。

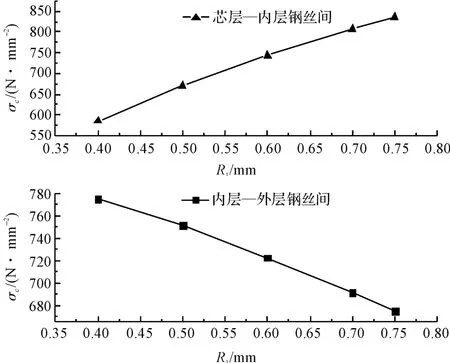
圖6 內層鋼絲半徑對接觸應力的影響

當內層鋼絲半徑從0.4 mm 變到0.75 mm，從圖6可知芯層鋼絲與內層鋼絲的接觸應力隨著內層鋼絲半徑增大而增大，內層鋼絲與外層鋼絲的接觸應力隨著內層鋼絲半徑增大而減少。

因此在設計繩股時，通過在一定范圍內選較大的內層鋼絲半徑，可使內、外層鋼絲的接觸應力減少，同時使各層鋼絲的接觸應力趨于均勻，延長使用壽命。

2.5 不同的外層半徑對接觸應力的影響

本研究對受軸向力4 500 N，芯層和內層鋼絲半徑分別為0.8 mm、0.6 mm，外層鋼絲半徑為0.2 mm ～0.6 mm，的單股鋼絲繩進行分析，得到的結果如圖7所示。

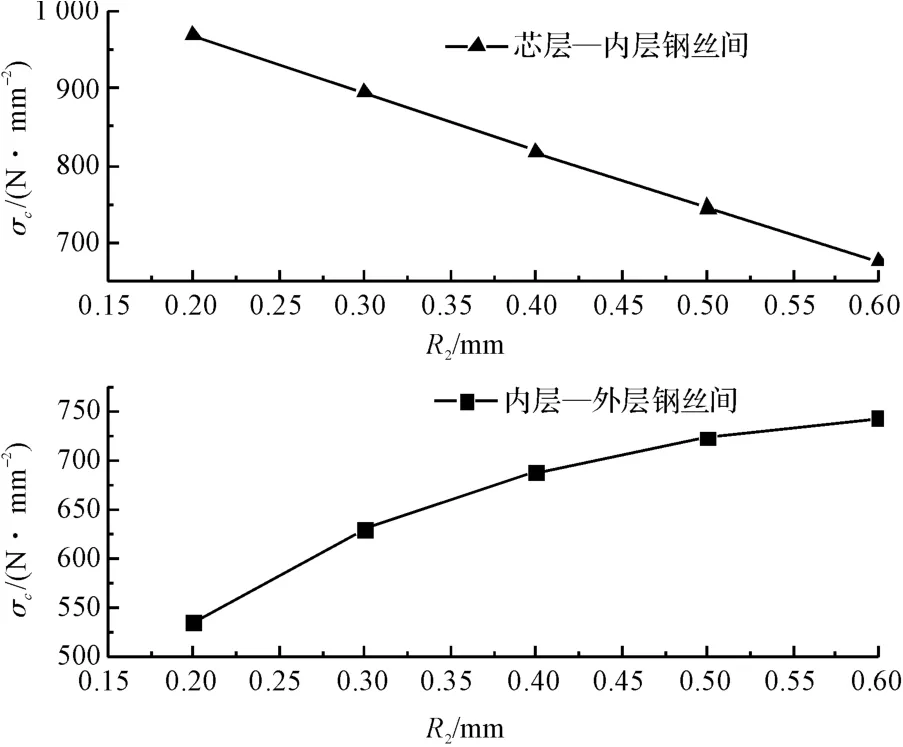
圖7 外層鋼絲半徑對接觸應力的影響

當外層鋼絲半徑從0.2 mm 變到0.6 mm，從圖7可知芯層鋼絲與內層鋼絲的接觸應力隨外層鋼絲半徑增大而減少，而內層鋼絲與外層鋼絲的接觸應力隨外層鋼絲半徑增大而增大。

因此，在一定范圍內選擇較大的外層鋼絲半徑，這樣可以使得芯內層鋼絲的接觸應力減少，同時使各層鋼絲之間接觸應力趨于均勻，從而大大延長了電梯曳引鋼絲繩的壽命。

3 電梯曳引鋼絲繩拉伸實驗

3.1 拉伸實驗

拉伸實驗主要是用來考核鋼絲的抗拉強度。該實驗采用SHT4 型微機控制電液伺服萬能試驗機(如圖8(a)所示)對鋼絲繩進行靜態拉伸實驗。該試驗機主要由主機、液壓源、DCS 控制器、計算機數據處理系統等部分組成。

圖8 微機控制電液伺服萬能試驗機及基本參數設置

主運動驅動是由電機供電驅動液壓泵通過伺服閥推動主油缸及活塞運動，從而拉壓夾具。

電梯鋼絲繩的繩頭組合是采用自鎖緊楔型，安裝好鋼絲繩后，進入試驗窗口，設計試驗參數，給鋼絲繩加載，拉伸一段時間之后，拆下鋼絲繩，先對鋼絲繩進行拆股并觀察分析。

該試驗采用位移控制方式，按照位移速度30 mm/min，加載力到58 000 N，引伸計的切換采用手動形式，試驗入口力前將采用開度運行，其開度值為200 N，參數設置界面如圖8(b)所示。本研究按上述實驗要求對直徑10 mm 8 ×19 麻芯鋼絲繩進行拉伸實驗。

從圖9 反映了鋼絲在拉伸過程中彈性階段和上、下屈服點，由實驗得知其拉破斷力是45.838 kN。

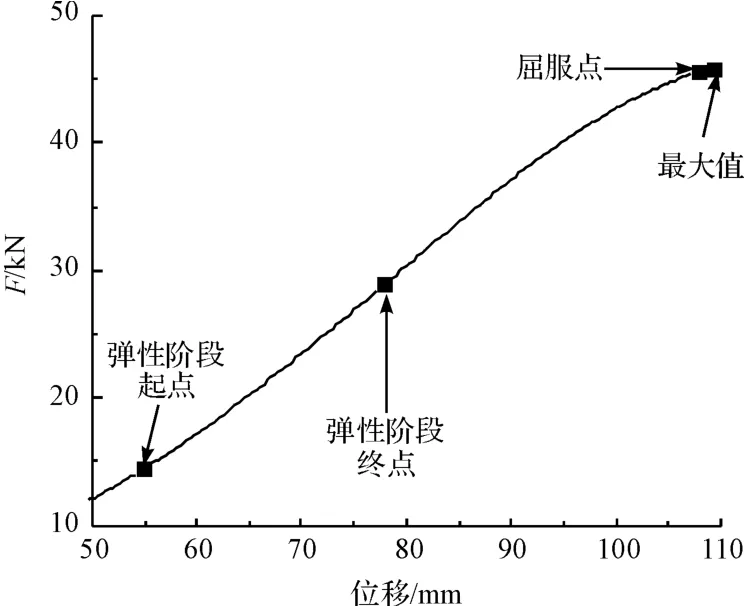
圖9 力隨位移的變化(特征點說明)

3.2 實驗結果分析

從電梯鋼絲繩拉伸試驗的過程中看，本研究在最后將要拉斷的時候，有力值下降的過程，停機觀察鋼絲繩，剛開始力有下降，說明有斷絲，發現外層表面鋼絲未斷裂，可以斷定有內部有鋼絲斷裂，但隨著時間推移，鋼絲表面出現斷裂，最后整股鋼絲斷裂。鋼絲某一階段以及拉斷后情況如圖10所示。從斷裂的順序可以間接驗證前面理論的接觸應力大小順序的正確性。

圖10 鋼絲某一階段以及拉斷后情況

從前面分析可知，電梯曳引鋼絲繩受力作用時，由于其各層受力不均，芯股(麻芯)與側股間的鋼絲接觸應力大，對于側股來說，芯層與內層鋼絲之間接觸應力相對于內層與外層之間要大一些。理論上，由于電梯曳引鋼絲繩股間的接觸應力大，其內部潤滑條件不好，電梯曳引鋼絲繩在接觸應力下，其將發生較大的磨損。為進一步驗證理論分析鋼絲繩內部磨損的正確性，本研究對試驗后的電梯曳引鋼絲繩樣繩，將其進行拆股試驗，以分析其內部磨損情況。筆者用螺絲刀拆開，電梯曳引鋼絲繩解剖圖如圖11所示。

圖11 電梯曳引鋼絲繩解剖圖

單股鋼絲繩解剖圖如圖12所示。

圖12 單股鋼絲繩解剖圖及局部鋼絲表面情況

該電梯曳引鋼絲繩為麻芯結構，工況試驗后，本研究取一股未斷裂的鋼絲觀察分析，其外表面有磨損;在側股與芯股接觸處，側股外層表面不光滑，有較深磨損點，用手觸摸有刺感比較粗糙(電梯曳引鋼絲繩解剖圖如圖11所示);在側股中芯層與內層鋼絲接觸處，芯層與內層鋼絲接觸處磨損較為嚴重，有磨損點(單股鋼絲繩解剖圖及局部鋼絲表面情況如圖12所示);內層與外層鋼絲之間磨損量相對較小，外層鋼絲只在與麻芯鋼絲接觸處存在磨痕，其磨痕深度較深，這磨損情況與計算的結果是一致的，進一步說明電梯曳引鋼絲繩受力分析理論的正確性。

4 結束語

本研究對單股1 ×19 結構和整根8 ×19 結構的電梯曳引鋼絲繩建立力學模型，并進行了力學分析。對于單股電梯鋼絲繩(1 ×19):芯層鋼絲的軸向力最大，其次是內層鋼絲的軸向力，外層鋼絲繩的軸向力最小;其芯層與內層鋼絲的接觸應力大于內層與外層之間的鋼絲。對于8 ×19 結構的電梯曳引鋼絲繩(繩芯為麻芯):芯股與側股之間最大，側股內芯層與內層之間次之，側股內內層與外層之間的最小;并且通過電梯曳引鋼絲繩拉伸后拆股實驗驗證其理論的正確性，同時分析了單股各層鋼絲半徑對接觸應力的影響，為后續的電梯鋼絲繩設計及研究奠定基礎。

由于該研究未考慮同層鋼絲之間接觸情況，下一步將通過有限元等方法進行深入研究。

［1］ERDONMEZ C，IMRAK C E.A finite element model for independent wire rope core with double helical geometry subjected to axial loads［J］.Sadhana，2011，36(6):995-1008.

［2］USABIAGA H，PAGALDAY J M.Analytical procedure for modelling recursively and wire by wire stranded ropes subjected to traction and torsion loads［J］.International Journal of Solids and Structures，2008，45(21):5503-5520.

［3］STANOVA E，FEDORKO G，FABIAN M，et al.Computer modelling of wire strands and ropes Part I:Theory and computer implementation［J］.Advances in engineering software，2011，42(6):305-315.

［4］王曉宇，王 雷，孟祥寶.圓股鋼絲繩幾何建模與力學分析的探討［J］.礦山機械，2013(9):55-60.

［5］孫建芳.鋼絲繩捻制成形數值模擬與制品力學強度分析［D］.武漢:華中科技大學塑性成形模擬與模具技術國家重點實驗室，2004.

［6］劉玉輝，寇子明，吳 娟，等.單捻鋼絲繩股內鋼絲應力分布研究［J］.礦山機械，2014，42(2):45-48.

［7］許波波.摩擦提升首繩力學分析［J］.煤礦現代化，2013，(2):81-83.

［8］COSTELLO G A.Theory of wire rope［M］.Berlin:Springer，1997.

［9］FEYRER K.Wire ropes［M］.Berlin:Springer-Verlag Berlin Heidelberg，2007.

［10］陳 杰.Matlab 寶典［M］.北京:電子工業出版社，2009.