基于FPGA的磁懸浮微驅動器控制系統研究*

楊莉莉，郭 亮

(浙江理工大學機械與自動控制學院，浙江杭州310018)

0 引言

微驅動器是指能產生精度較高的驅動力器件或裝置，其作為微機電系統(MEMS)的核心部件，廣泛存在于微小機器人的活動關節、微小航天儀器、磁盤驅動、超精密加工等方面，因此對微驅動器的測量控制研究顯得尤為重要［1-2］。由于傳統的接觸式、氣浮式微驅動器難以在定位精度、運動自由度等方面實現更高的設計要求，磁懸浮式微驅動器以其優越的定位性能受到了廣泛關注，并在精密微小領域獲得了更大的發展。磁懸浮微驅動器系統是一個非線性、參數攝動、耦合、抗干擾能力差的精密復雜系統［3-4］，對于動子多自由度的運動控制是由單個自由度運動控制結合而成的，因此完成動子多自由度精確定位的重要基礎是動子的無靜差穩定懸浮。

本研究主要實現對磁懸浮微驅動器懸浮狀態的精確控制，傳統控制系統中常采用PC 或DSP 進行控制，PC 控制系統中外部數據采集卡的采樣頻率較低，難以滿足高速數據處理的要求，進而無法實現高精度控制的目的;DSP 運算速度快，合適處理密集的加乘運算［5］，但用戶可自定義管腳過少，不利于實現對多相電機的控制。而FPGA 以其高時鐘頻率著稱，不僅內部延時小，能并行運行程序完成大量數據運算，而且擴展性較好，便于后續控制系統功能的升級［6-7］，經過綜合分析比較后，選擇型號為EP2C5T144I8 的FPGA 作為主控芯片，用于實現磁懸浮微驅動器的懸浮系統控制。

本研究針對日磁懸浮微驅動器的實時精確控制問題，對FPGA 的磁懸浮微驅動器進行了研究。

1 磁懸浮微驅動器

1.1 磁懸浮微驅動器結構

層疊繞組式磁懸浮微驅動器的結構如圖1所示，它由背鐵、塑膠板、空心繞組及定子永磁陣列等4 部分組成。其中:定子部分的永磁體采用二維Halbach 的永磁矩陣結構，該矩陣由形狀尺寸完全相同的109 塊釹鐵硼材料制成的永磁體模塊和12 塊鐵塊組成，動子部分采用層疊式空心繞組的結構，四層繞組正交疊加，自上而下的四層導線中第一、三層沿y 方向鋪設，第二、四層沿x 方向鋪設［8］。

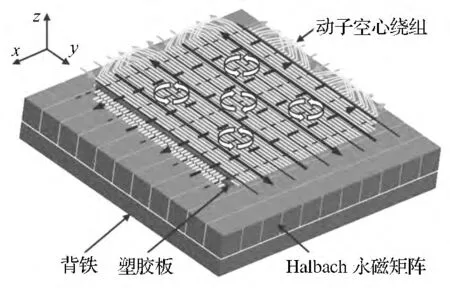
圖1 磁懸浮微驅動器結構

1.2 磁懸浮微驅動器工作原理

動子線圈采用相互間隔的直導線的形式排列，通過改變動子導線中的通電電流的大小和方向，即可改變動子導線板受到的洛侖茲力，從而改變動子的懸浮狀態。

本研究以圖1 中最底層的沿x 方向排列的直導線為對象進行分析，該層動子導線板與永磁體的位置關系如圖2所示。相鄰實線之間的導線電流方向相同，磁場為水平方向。筆者將水平充磁磁塊上方虛線間的繞組設置為懸浮力控制繞組，其余繞組則設置為水平推力控制繞組;改變懸浮力控制繞組的電流即可實現動子直導線板的懸浮定位和繞x 軸旋轉，而改變水平力控制繞組的電流即可實現其y 方向的平動，同理可對y 方向排列的空心繞組進行分析，并由此得出結論。通過控制繞組中的電流可實現動子線圈5 個自由度的運動，分別為沿x、y、z 軸平移以及繞x 軸、y 軸旋轉。

1.3 磁懸浮微驅動器動子運動模型

為了避免懸浮過程中動子線圈其他自由度方向的運動，本研究利用滾珠直線軸承把動子線圈固定在4根垂直桿上，使其只能進行z 方向運動。通過對動子線圈的電流控制調整后使得每根導線中電流元受到的洛倫茲力方向向上。以動子導線板的位移、運動速度以及電流為變量，根據洛倫茲力、電路原理以及運動學相關原理可知，懸浮微驅動器動子的運動模型如下:

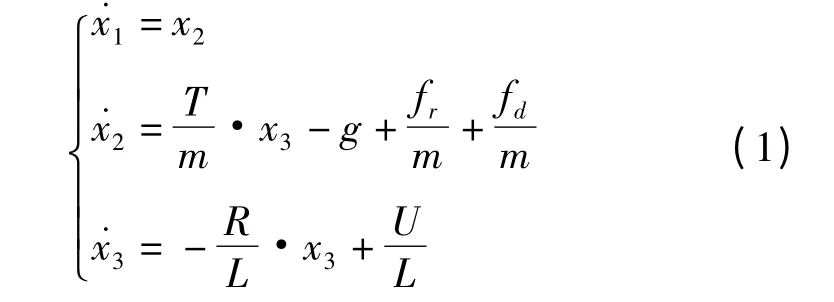
式中:T—磁場強度;g—重力加速度;fr—動子導線板所受的摩擦力;fd—系統所受到的外部干擾;l—磁場中每根導線的長度;m—動子導線板質量，其值為313.36 g;R—單根導線電阻，其值為0.7 Ω;L—直導線形成的等效電感，其值為84.3 μH;U—系統輸出的控制電壓。

2 PID 控制仿真

PID 控制通過對誤差進行比例、積分、微分調節，具有參數調整方便、結構簡單、穩定性好等優點［9］。為減小計算過程中產生的誤差，本研究對PID 算法進行離散化后分別得到第k 次和第k－1 次控制算式，兩式相減后得到增量型PID 控制算法公式如下式所示:

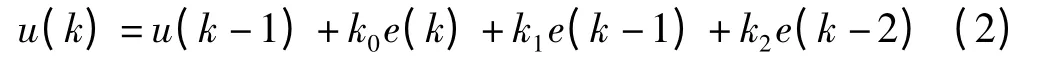
式中:KP、Ki、Kd—比例、積分、微分環節對應的參數，系數k0= Kp+ Ki+ Kd，k1=－ Kp－2Kd，k2= Kd，e(k)、e(k－1)和e(k－2)分別為第k、k－1 和k－2 次測量偏差。

筆者通過Matlab 對微驅動器運動模型進行PID控制仿真，其仿真模型如圖3所示。結合Signal Constraint 調節PID 參數，仿真出的PID 參數為KP=10.986 1，Ki=2.704 3，Kd=0.070 7，PID 參數下系統的1 mm階躍響應仿真波形如圖4所示。仿真結果的超調為4%，整定時間0.06 s，穩態誤差小于1%。

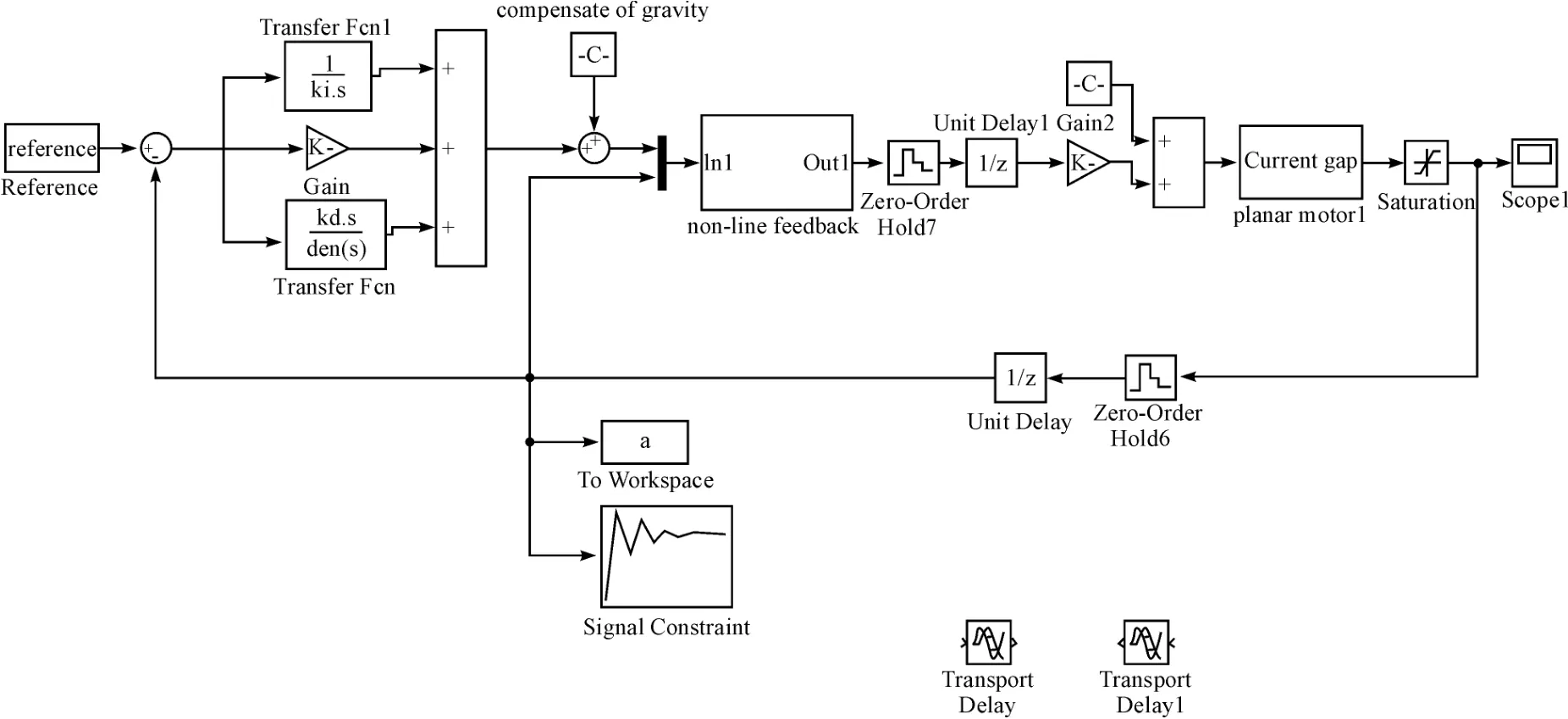
圖3 PID 控制仿真模型

圖4 PID 仿真波形

3 控制系統硬件設計

為實現動子無靜差懸浮和快速響應，需設計硬件系統將采集到的動子懸浮氣隙高度轉化為電壓信號，經過數據處理后將控制信號傳輸給動子線圈，從而實現整個系統的閉環控制。控制系統選用渦流傳感器KD2306-2S1 測量動子懸浮高度，輸出的位移信號經A/D 轉化為數字量后傳輸至FPGA 中，數字信號在FPGA 中完成濾波算法，通過電壓轉換后完成PID 控制算法，最后由FPGA 將控制信號發送給DA 并輸出至驅動器，從而完成驅動平面電機動子的工作。同時需要將采集到的電壓信號傳輸至PC 機并轉化成動子線圈的懸浮高度，實時顯示在上位機界面上，觀察響應時間、超調量、波動等信息，驗證控制效果。系統硬件框圖如圖5所示。

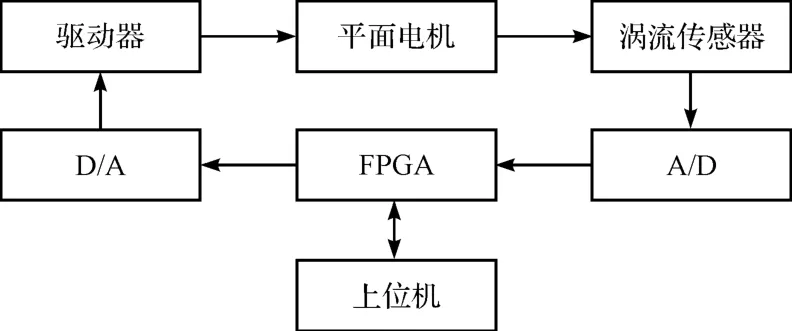
圖5 系統硬件框圖

3.1 A/D 采樣電路

A/D 采樣電路中使用的ADC 芯片AD7671AST 為16 位逐次逼近式高精度模數轉換器，其最高采樣速率可達1 MSPS。為了驅動AD7671 且保持其SNR 和轉換噪聲的性能，選擇低噪聲、高增益帶寬的OP07AZ 作為輸入緩沖器，并接入10 pF 的外部補償電容。2.5 V參考電壓由電源轉換芯片ADR421 提供。OVDD 輸入引腳設置為數字3.3 V 以匹配FPGA 的端口電壓［10-11］。

(1)WARP 和IMPLUSE 配置為低電平，使AD7671工作于NORMAL 模式;

(2)SER/PAR 配置為低電平，使采樣電路輸出16位并行信號;

(3)采集的微驅動器懸浮信號的范圍為－10 V ～10 V，依據模擬輸入配置表將INA 接參考電壓REF，INB、INC 接模擬地、IND 接模擬輸入;

(4)CS、CNVST、RD、BUSY 控制引腳和16 位DATA 數據引腳分別與FPGA 各引腳相連，完成AD7671的采樣過程。

3.2 DA 數據輸出電路

DA 芯片選用16 位串行高速數模轉換芯片AD5545，為了輸出±5 V 的信號，DA 輸出口外接高精度運算放大器AD8620，運算放大電路中選用0.01%精度的電阻以提高輸出精度。FPGA 通過CS、RS 及LDAC控制信號將數據從SDI 引腳輸出至DA，完成驅動控制。

4 控制系統軟件設計

FPGA 內部邏輯控制模塊主要包括ADC 采樣模塊、FIFO［12］模塊、濾波模塊、PID 控制模塊、DAC 數據輸出模塊及RS-232 通信模塊，FPGA 邏輯控制軟件的整體框圖如圖6所示。

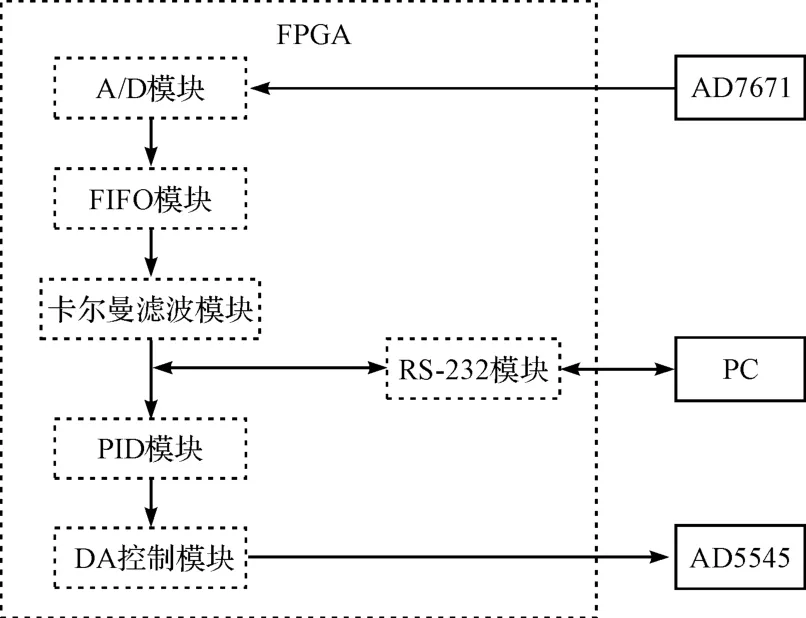
圖6 軟件控制系統框圖

4.1 A/D 采樣控制模塊

A/D 采樣時序由FPGA 控制產生，而時鐘信號由AD7671 內部自己產生。CNVST 低電平時啟動轉換，完成信號讀取，兩個時鐘周期后使CNVST 為高電平，進入數據保持階段，BUSY 為AD7671 的反饋信號，一旦A/D 開始轉換，則變為高電平，在BUSY 為高電平時選通RD 并讀取上一次轉換數據。狀態機初始狀態為S0，此時RD 和CS 為高電平狀態，CNVST 為低電平，將CS 變為低電平，CNVST 變為高電平后，進入S1狀態，即開始模數轉換，等待1 個時鐘周期后進入S2狀態判斷BUSY 是否為高電平，是則進入S3 狀態，將RD 變為低電平，并開始讀取轉換結果;否則繼續等待，讀取完成后返回S0 狀態。

4.2 FIFO 緩存模塊

為解決A/D 數據采集速度和后續卡爾曼濾波器運算速度匹配問題，本研究通常在中間加入FIFO 緩存器。FIFO 緩存模塊為四級緩存，該模塊分別檢測寫信號和讀信號，檢測到寫使能信號且寄存器未滿時，將數據保存至寄存器，同理，檢測到讀使能信號時完成從寄存器中讀取數據。

4.3 卡爾曼濾波模塊

卡爾曼濾波是用一組遞歸方程組來估計系統的狀態。卡爾曼濾波方法計算速度快，占用內存少，滿足磁懸浮控制系統實時性的要求，當信號和噪聲同時輸入時，卡爾曼濾波器能在保留信號的同時，最大程度抑制噪聲［13］。卡爾曼濾波算法步驟如下:

(1)設置系統初始估計值X0，初始均方誤差陣P0和初始信號值Zk;

(2)由式(4)計算出預測誤差Pk|k－1;

(3)再根據式(5)計算出濾波增益Kk;

(4)將數據代入(3)可得最優預測值Xk|k－1;

(5)最后根據以上數據通過式(7)計算出最優濾波估計值Xk，同時根據公式(6)更新Pk的值。

通過步驟(1)～(5)完成了一次濾波周期算法，卡爾曼濾波計算公式如下:

(1)最優預測值:

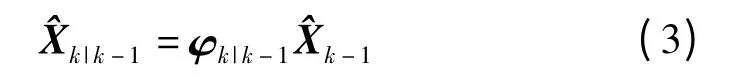
(2)預測誤差協方差:

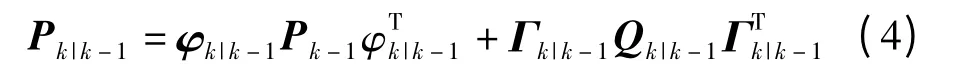
(3)濾波增益矩陣:

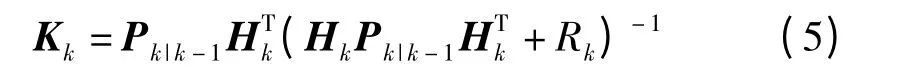
(4)估計誤差協方差:

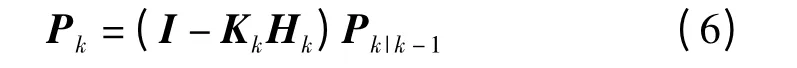
(5)最優濾波估計值:

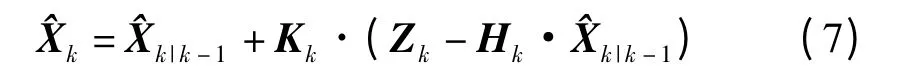
4.4 PID 算法控制模塊

PID 算法選擇并行方式實現，采用增量式算法將PID微分方程分解為FPGA 易實現的基本運算式，以便于將運算器和數據類型進行歸一化處理，達到減少運算算子的目的。對并行結構方法進行改進的運算思路如下:

(1)減法運算通過二進制補碼形式實現，即A－B=A+(B 補);

(2)擴展加法運算位數，同符號數相加時可能出現運算結果位數溢出，因此在數據運算中將數據結果擴展一位;

(3)由于FPGA 不支持浮點運算，故將浮點數轉換成定點數進行運算;

(4)FPGA 只能進行整數運算，為保留采樣數據的精度，計算時需要將實數轉換為整數，即將數據擴大10n使小數轉化為整數，計算后再使輸出結果縮小10n作為輸出信號;

(5)寄存器REG 可鎖存信號，3 路信號并行計算減少了延時時間，提高了運算的速率。

筆者根據公式(2)對期望值r(k)與測量值y(k)的偏差e(k)進行PID 運算，其中系數k0、k1、k2均由仿真得出，與改進后的并行結構共需要4 個加法器、3 個乘法器，比傳統并行結構少用了3 個減法器，不僅減少了連線數量，且提高了對設計的加法IP 核的利用率，降低了設計的難度，提高了工作效率。

4.5 DA 控制模塊

DA 控制輸出狀態機初始狀態為S0，此時CS =0，LDAC=0;CS 與LDAC 均變為高電平后，進入S1 狀態;CS 上升沿觸發DAC 輸入，將包括地址信號在內的18 位數據傳輸至DAC 內部的輸入寄存器中，然后進入S2 狀態，此時計數器開始從0 ～18 的計數，保證DAC 完成輸入寄存器的數據串行移位至DAC 寄存器;改變CS 和LDAC 的電平，使CS 和LDAC 變為低電平，進入S3 狀態，完成數模轉換并輸出。

4.6 RS-232 通信模塊

FPGA 與上位機通信采用RS-232 通信方式，波特率設定為9 600，即接收一個bit 的時間為1 s/9 600 =104 μs。由于FPGA 的晶振為50 MHz，故可用50 M 時鐘設計計數器，并根據計數器發送數據，一次完整數據接收需要有1 144 000 ns，所以計數器必須計滿57 200次，所以需要16 位計數器。由于A/D 采樣得到的數據為16 位，而RS-232 一次最多傳送8 位，本研究將16位數據分成兩部分，高、低8 位依次經過RS-232 與上位機通信。

5 實驗及結果分析

為驗證磁懸浮控制系統的可行性，筆者搭建實驗平臺。磁懸浮平臺的動子表面積略大于永磁體，邊長大約為120 mm，動子板的4 個角通過滾珠式直線軸承與豎直導軌相連，使動子只產生z 方向位移，導軌上安裝渦流傳感器對懸浮高度進行實時測量，控制信號通過驅動器線性放大后轉化為微驅動器動子繞組的輸入電流信號，調節動子導線板與定子永磁體間相互作用的電磁力從而控制動子懸浮高度，上位機中實時顯示控制效果。磁懸浮控制實驗系統框圖如圖7所示。

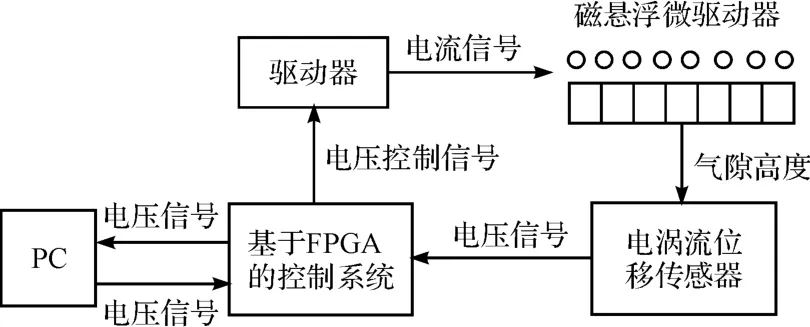
圖7 磁懸浮控制實驗系統框圖

在PID 控制器下的磁懸浮系統的1 mm 階躍響應實驗圖如圖8所示。系統頻率為10 kHz，通過分析曲線可知該系統的超調量為4.2%，整定時間為0.05 s，系統的穩態誤差為1 μm，與圖4 仿真結果基本一致。

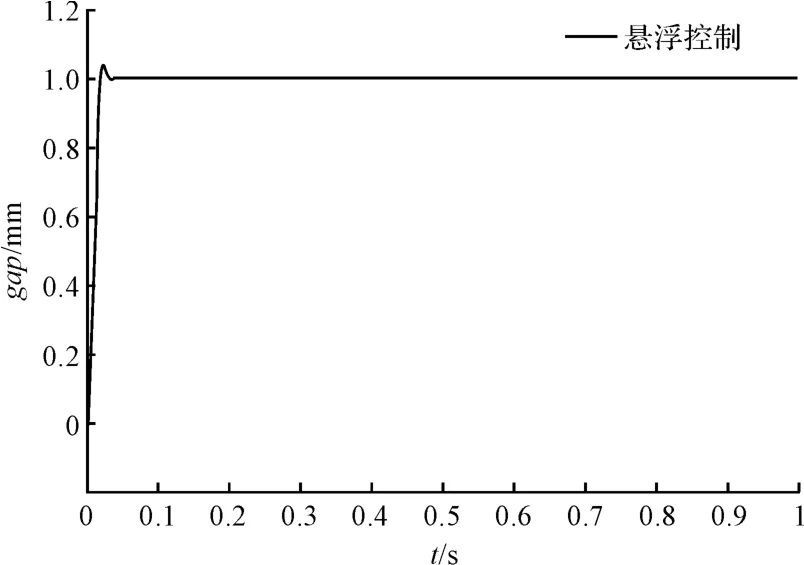
圖8 PID 控制下系統階躍圖

驗證磁懸浮控制系統的控制精度，控制系統在1 mm和1.7 mm 氣隙高度下1 μm 位移的多次階躍響應圖形如圖9所示。從圖9 中可以看出系統能快速作出反應且波動范圍在1 μm，基本能夠實現定位精度為1 μm的大范圍精確控制。

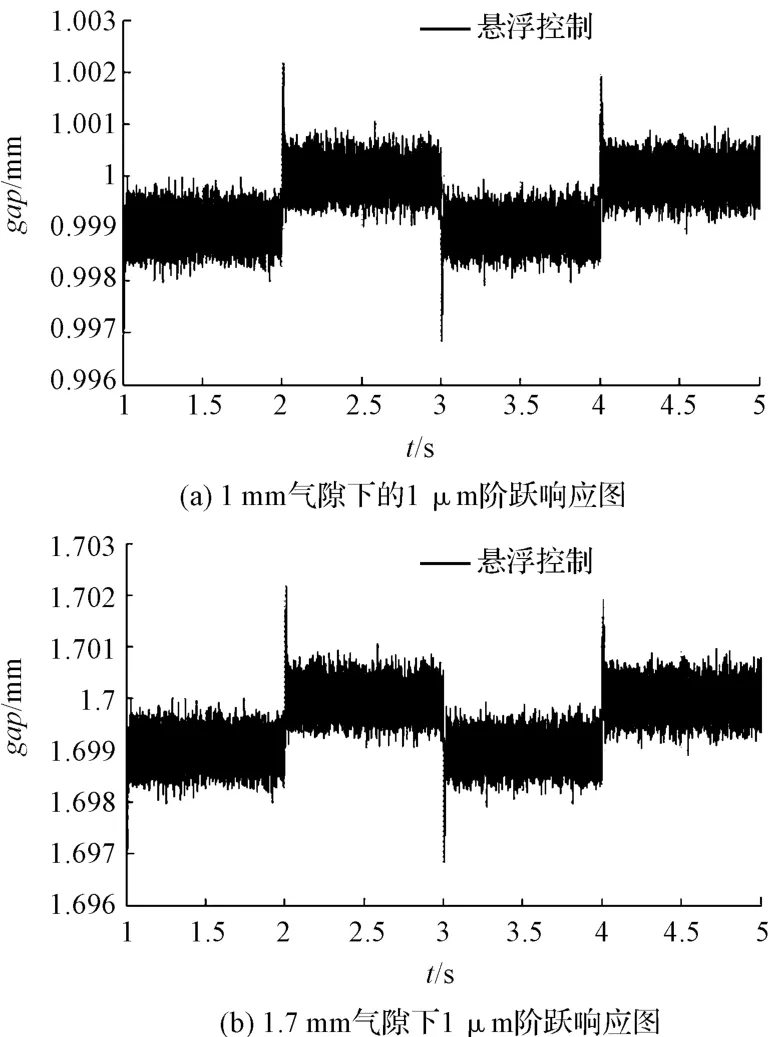
圖9 1 μm 階躍響應

然后驗證磁懸浮系統在PID 控制下的運動跟蹤能力，在1 mm 氣隙下對正弦目標信號的跟蹤實驗結果如圖10所示，系統對峰-峰值為20 μm，頻率為10 rad/s 的正弦信號跟蹤圖如圖10(a)所示，可看出系統符合預期曲線，跟蹤效果較好，對峰-峰值為2 μm，頻率為10 rad/s的正弦信號跟蹤圖如圖10(b)所示，可以看到動子運動圖形與預期正弦信號基本一致，并具有優良的實時性。

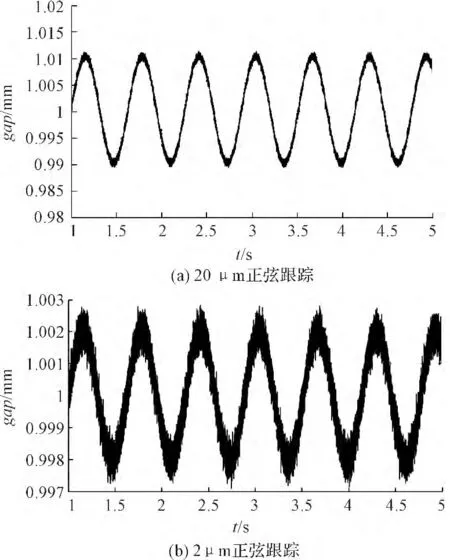
圖10 正弦跟蹤響應

6 結束語

該設計的硬件電路能對磁懸浮微驅動器懸浮運動模型進行精確的信號采集，PID 控制算法能切實有效地對懸浮信號進行閉環實時控制，通過搭建懸浮控制系統實驗平臺對磁懸浮微驅動器進行實時PID 控制實驗，通過將控制系統仿真數據與實驗數據進行對比可知，在1 mm 階躍響應中，系統上升過程和穩態過程幾乎完全相同，驗證了運動模型的準確性。通過對不同氣隙下的連續階躍響應和不同幅值的正弦跟蹤響應圖形可知，系統的反應速度快、跟蹤范圍大、跟蹤延遲和跟蹤誤差小、控制精度高，實現了2 mm 范圍內1 μm精度的懸浮微運動控制，在磁懸浮微驅動器微小定位方面有著良好的應用，為MEMS 的精密化方向發展墊定了基礎。

［1］趙立敏.MEMS 微驅動器的設計、工藝及應用［D］.西安:西安電子科技大學機電工程學院，2014.

［2］周海波.磁懸浮直線運動系統的設計與控制研究［D］.湖南:中南大學機電工程學院，2010.

［3］仇志堅，戴 軍，陳小玲.基于不完全微分PID 的斥力型磁懸浮平臺控制系統研究［J］.微特電機，2014，42(10):75-77.

［4］CHEN J，YANG S.Design of magnetic levitation micro-actuator positioning control system［J］.Application of Electronic Technique，2012，38(3):96-98.

［5］侯正男，蔣啟龍，劉 東.基于DSP 的交流磁懸浮穩定控制［J］.電力電子技術，2014，48(9):48-50.

［6］JASTRZEBSKO R，POLLANEN R，PYRHONEN O.Real-Time Emulator of Magnetic Suspension System for FPGAbased Controller［C］//Mechatronics，2006 IEEE International Conference on.IEEE，2006:98-103.

［7］柏 瀅，林 都，鮮 浩.基于FPGA+DSP 的數據采集與實時處理系統的設計［J］.傳感器世界，2014，20(10):27-31.

［8］張 釗.層疊繞組式磁懸浮永磁直流平面電機魯棒控制系統研究［D］.浙江:浙江理工大學機械工程學院，2014.

［9］李垂君.基于FPGA 的PID 控制器研究與實現［D］.遼寧:大連理工大學電子與信息工程學院，2008.

［10］李 蘇，李 輝.基于AD7671 的聲波采集電路設計［J］.石油工業計算機應用，2012(4):29-31.

［11］樊 凡，張 鵬.高精度模數轉換器AD7671 的原理及應用［J］.今日電子，2004(9):57-58.

［12］XIAO J.Implementation of asynchronous FIFO buffer based on FPGA［J］.Electronic Measurement Technology，2009，32(11):92-94.

［13］周 倩.車輛組合導航中卡爾曼濾波器的設計及FPGA實現［D］.北京:北京交通大學電子信息工程學院，2009.