一種主客觀結(jié)合的屬性權(quán)重確定方法
□ 陳燕云 季 丹 邱建林
一、引言
權(quán)重確定在決策過程中非常重要,它體現(xiàn)了各個(gè)屬性在評(píng)價(jià)過程中的地位,直接關(guān)系到最后的決策結(jié)果。目前已有許多專家學(xué)者對(duì)權(quán)重確定進(jìn)行了研究,比較常用的權(quán)重確定方法有模糊統(tǒng)計(jì)法、主觀賦值法如Delphi法、二元對(duì)比排序、模糊判斷矩陣法等等。單一的權(quán)重確定法或者偏主觀,或者又過于依賴于數(shù)據(jù),因此都無法全面反映屬性的重要程度。本文提出一種將偏主觀經(jīng)驗(yàn)的灰色關(guān)聯(lián)度法和“憑數(shù)據(jù)說話”的粗集權(quán)重確定法相結(jié)合的主客觀集成權(quán)重確定方法,在一定程度上改善了單一權(quán)重確定法的不足。
二、基于粗糙集理論的權(quán)重確定方法
常見的基于粗集理論的權(quán)重確定方法是通過計(jì)算決策屬性對(duì)條件屬性的依賴度來確定屬性的重要度,進(jìn)而確定屬性權(quán)重的。具體步驟如下:
決策系統(tǒng)S=(U,A,V,f),A=CYD 是屬性集合,C是條件屬性,D是決策屬性,則C與D之間的依賴度γc(C,D)為:
γc(D)表示了由條件屬性C的取值能準(zhǔn)確判定出屬于某個(gè)決策屬性D的等價(jià)類的對(duì)象所占系統(tǒng)的比例。任意cj∈C對(duì)D的重要性定義為:sigDC-{cj}=γ(C,D)-γ(C-{cj},D)。
這說明屬性cj∈C的重要程度可由去掉c后所引起的決策屬性依賴度變化的大小來度量。
第j個(gè)屬性cj的權(quán)重
目前已有不少算法對(duì)該經(jīng)典算法作出了改進(jìn)。文獻(xiàn)綜合考慮了屬性集中條件屬性的整體重要度和個(gè)體重要度,改善了常見冗余屬性為0引起的矛盾。文獻(xiàn)在考慮冗余屬性權(quán)重的同時(shí)通過設(shè)置高級(jí)優(yōu)先隊(duì)和低級(jí)優(yōu)先隊(duì)來避免出現(xiàn)冗余權(quán)重大于非冗余權(quán)重的情況,確保權(quán)重的合理性。
然而有時(shí)候我們求信息系統(tǒng)的權(quán)重,即數(shù)據(jù)表中沒有決策屬性,需要單從條件屬性出發(fā)解決權(quán)重的分配問題。
本文采用基于條件信息熵的權(quán)重確定方法,具體步驟如下:
設(shè)信息系統(tǒng) S=(U,A),A={A1,A2,Λ,An},令 X=U/IND(Aj)={X1,X2,Λ,Xm}表示等價(jià)關(guān)系 IND(Aj)在 U 上的劃分,

定義屬性Aj的信息熵H(Aj)為:
H(Aj)=-∑mi=1P(Xi)log2(P(Xi))
進(jìn)而,屬性Aj的權(quán)重定義為:
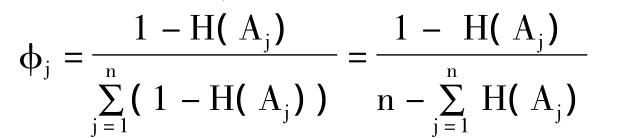
總之,基于粗糙集理論的權(quán)重確定方法完全是由數(shù)據(jù)決定的,比較客觀,但粗糙集理論對(duì)樣本數(shù)據(jù)的要求比較高,如果樣本數(shù)據(jù)不具有代表性,其決定的權(quán)重也會(huì)偏離實(shí)際。
三、灰色關(guān)聯(lián)度權(quán)重確定方法
經(jīng)典的灰色關(guān)聯(lián)度權(quán)重確定步驟如下:
(一)構(gòu)建評(píng)價(jià)矩陣A,并無量綱化處理得矩陣C。
A=(aij)n×m;
Cij(k任意確定,且aik≠0)
(二)求取屬性兩兩之間的關(guān)聯(lián)度并構(gòu)建關(guān)聯(lián)度矩陣R。
εij(一般 =0.5)
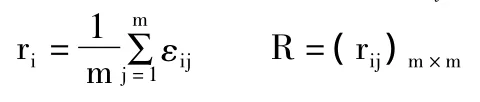
(三)計(jì)算各屬性的權(quán)重。
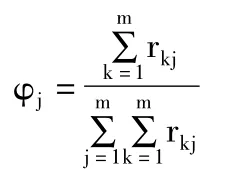
該算法中分辨系數(shù)ρ的取值具有主觀不確定性,使得灰色關(guān)聯(lián)度算法受專家決策的影響較大。
四、綜合權(quán)重的確定
綜合權(quán)重wj=αφj+(1-α)φj;α為經(jīng)驗(yàn)因子。
可以通過設(shè)置經(jīng)驗(yàn)因子,調(diào)整主觀權(quán)重和客觀權(quán)重的比重。
五、應(yīng)用
我們以屬性約簡(jiǎn)后的玉米樣本集為例,將上述提出的主客觀集成權(quán)重確定算法應(yīng)用到玉米良種選育當(dāng)中,如表1所示,共有7個(gè)屬性,51個(gè)對(duì)象。
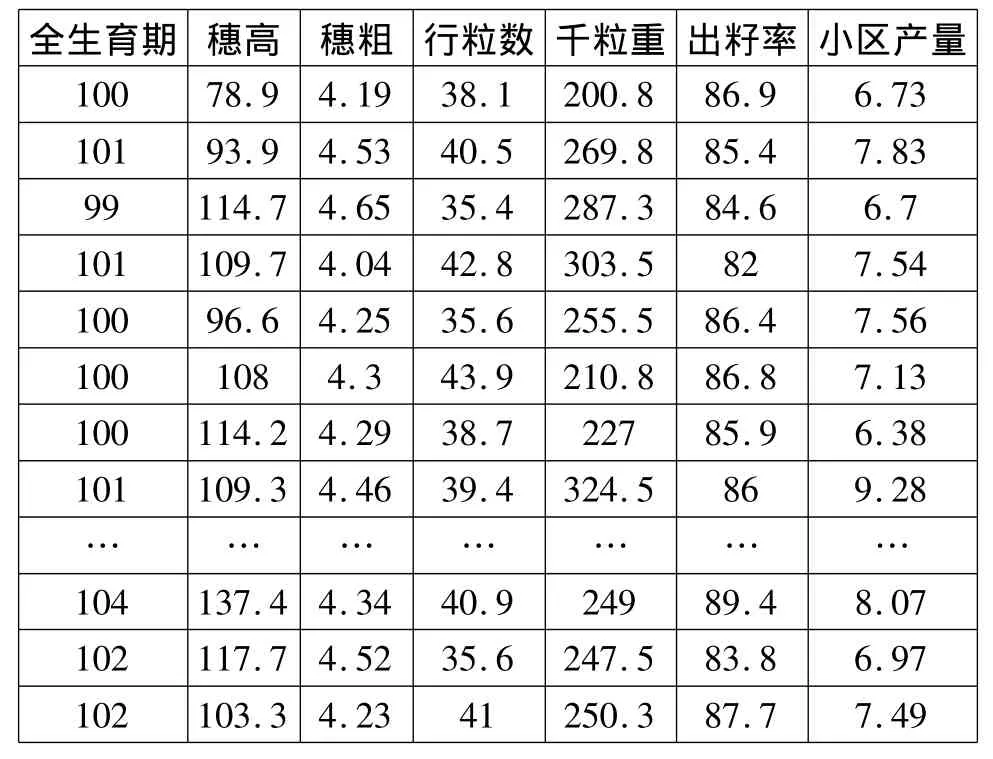
表1 玉米樣本集
(一)求粗糙集權(quán)重。七個(gè)屬性的信息熵分別求得為:1.3325、1.5736、1.5833、1.5699、1.5427、1.5801、1.397。
求得結(jié)果見表2。
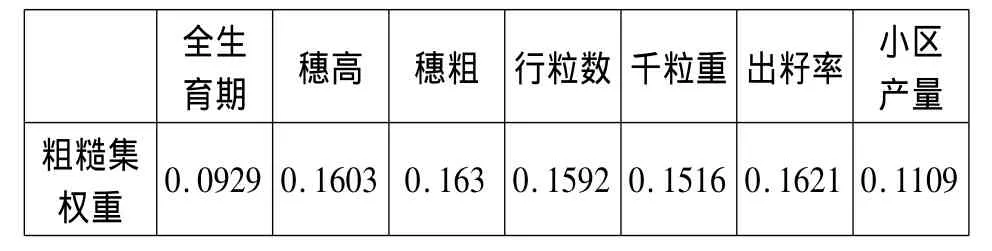
表2 粗糙集權(quán)重
(二)灰色關(guān)聯(lián)度權(quán)重。
1.求取標(biāo)準(zhǔn)化矩陣。因?yàn)楦鲗傩缘牧炕邓诘膮^(qū)間不完全相同,因此首先要進(jìn)行無量綱化處理,這里令第一行屬性值為1,其余行屬性值,結(jié)果見表3。
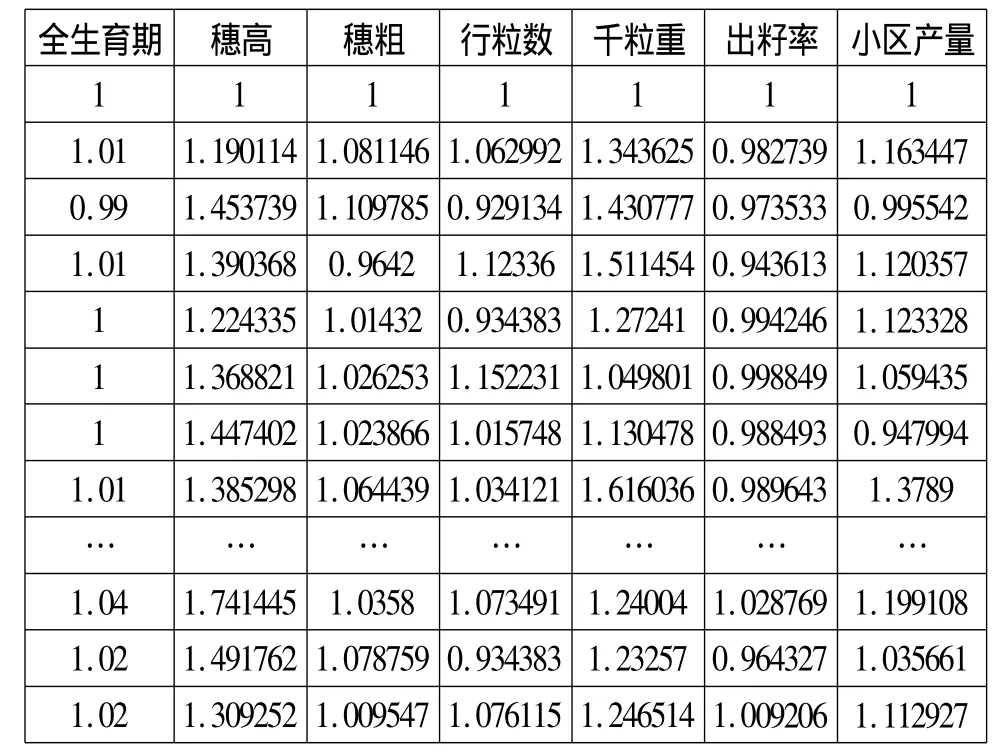
表3 標(biāo)準(zhǔn)化矩陣
2.構(gòu)建關(guān)聯(lián)度矩陣。如表4所示。

表4 關(guān)聯(lián)度矩陣
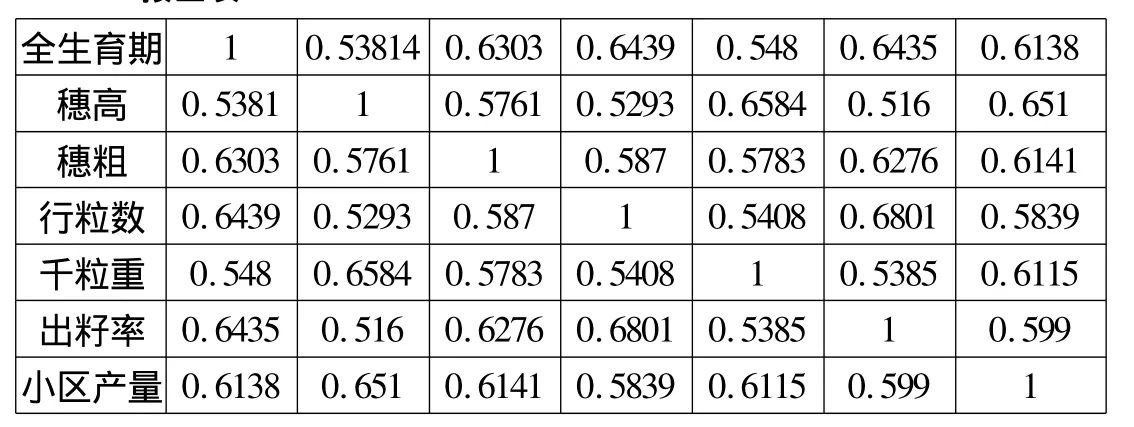
全生育期 1 0.53814 0.6303 0.6439 0.548 0.6435 0.6138穗高 0.5381 1 0.5761 0.5293 0.6584 0.516 0.651穗粗 0.6303 0.5761 1 0.587 0.5783 0.6276 0.6141行粒數(shù) 0.6439 0.5293 0.587 1 0.5408 0.6801 0.5839千粒重 0.548 0.6584 0.5783 0.5408 1 0.5385 0.6115出籽率 0.6435 0.516 0.6276 0.6801 0.5385 1 0.599小區(qū)產(chǎn)量 0.6138 0.651 0.6141 0.5839 0.6115 0.599 1
3.各屬性的灰色關(guān)聯(lián)度權(quán)重。如表5所示。
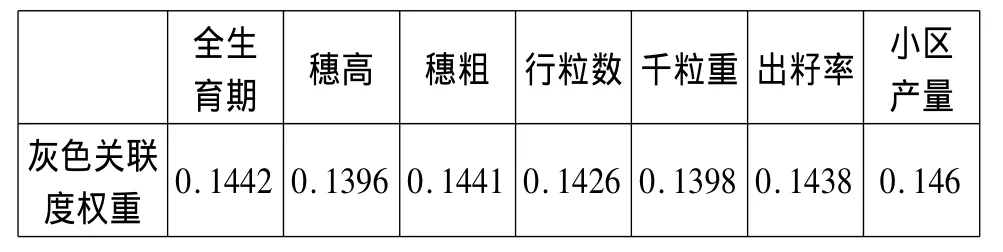
表5 灰色關(guān)聯(lián)度權(quán)重
(三)綜合權(quán)重。令 α =0.5,則 ω =0.5φ +0.5φ,因而綜合權(quán)重為:
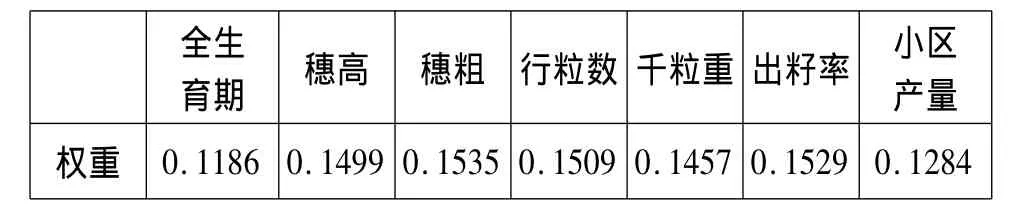
表6 綜合權(quán)重
三個(gè)權(quán)重對(duì)比見表7。

表7 權(quán)重對(duì)比
可以看出粗糙集權(quán)重和灰色關(guān)聯(lián)度權(quán)重的側(cè)重點(diǎn)并不相同,具有互補(bǔ)性,將它們結(jié)合起來得出的綜合權(quán)重更具合理性和實(shí)用價(jià)值。
六、結(jié)語(yǔ)
單一的賦值法在效果上或者偏主觀或者偏客觀,本文選取偏主觀的灰色關(guān)聯(lián)度權(quán)重確定法和偏客觀的粗糙集權(quán)重確定法,將兩者有效結(jié)合從而確定信息系統(tǒng)的綜合權(quán)重,在一定程度上改善了單一賦值法的不足,提高權(quán)重的合理程度,從而使最終決策更加準(zhǔn)確。但文中經(jīng)驗(yàn)因子的設(shè)置不夠科學(xué),需要進(jìn)一步研究。
[1]Mareschal B.Weight stability intervals in multi-criteria decision[J].European Journal of Operational Research,1998
[2]周宇峰,魏法杰.基于模糊判斷矩陣信息確定專家權(quán)重的方法[J].中國(guó)管理科學(xué),2006
[3]鮑新中,劉澄.一種基于粗糙集的權(quán)重確定方法[J].管理學(xué)報(bào),2009
[4]朱紅燦,陳能華.粗糙集條件信息熵權(quán)重確定方法的改進(jìn)[J].統(tǒng)計(jì)與決策,2011
[5]鄒永紅,譚建林.基于綜合灰色關(guān)聯(lián)度加權(quán)法的玉米品種評(píng)價(jià)[J].南方農(nóng)業(yè)學(xué)報(bào),2011
- 產(chǎn)業(yè)與科技論壇的其它文章
- 新形勢(shì)下基層領(lǐng)導(dǎo)干部心理問題的調(diào)適
- 醫(yī)院財(cái)務(wù)風(fēng)險(xiǎn)的防范與控制
- 我國(guó)商業(yè)銀行個(gè)人住房貸款的風(fēng)險(xiǎn)及對(duì)策探索
- 權(quán)力不是一種可以任意享受的權(quán)利——從“四風(fēng)”的思想認(rèn)識(shí)根源上防止其反彈回潮
- 基于大學(xué)科技園的互聯(lián)網(wǎng)創(chuàng)新創(chuàng)業(yè)孵化體系構(gòu)建——以南京郵電大學(xué)國(guó)家大學(xué)科技園為例
- 高校工會(huì)職能的構(gòu)建與完善

