基于改進矩陣束算法的水輪機控制系統參數辨識

劉俊敏，李興源，王 曦，丁理杰

（1.四川大學電氣信息學院，成都 610065；2.四川電力科學研究院，成都 610065）

0 引言

隨著電力系統的規模越來越大，運行狀態越來越復雜，電網安全及其穩定運行問題的重要性也日益突出。水電機組的運行狀況對維持電網頻率的穩定和安全至關重要，水輪機控制系統參數的設置不當將嚴重影響水電機組調頻功能的發揮，因此對水輪機控制系統參數的辨識是不容忽視的[1]。

目前，針對連續系統直接進行參數辨識存在的微分信號不易獲得且對其近似處理會加劇噪聲的問題[2]，專家學者們進行了廣泛的研究。常用的參數辨識方法有最小二乘法、prony算法等。基于最小二乘法的參數辨識需對連續的時間系統進行離散處理，存在原理和計算方面的誤差，使得辨識結果不準確。而 prony算法由于其系統模態階數難以確定，所以辨識過程復雜且結果不能盡如人意[3-5]。

近年來，矩陣束算法被廣泛應用于連續系統參數辨識，且在電力系統分析和控制及信號處理等多個領域的應用中取得了不錯效果。矩陣束算法采用內積形式，有較強的抗噪能力，且其運算屬于非迭代過程，不存在迭代解法中初值限定、累積誤差及高運算量等問題，是一種高效實時的計算方法[6-7]。文獻[6]利用矩陣束算法實現對同步電機參數的準確辨識，文獻[7]利用改進的矩陣束算法對電力系統振蕩模態進行分析研究，提高參數辨識的精度，減少計算量。本文將改進矩陣束算法進行拓展，將其應用于水輪機控制系統的參數辨識中，在 Matlab中編制辨識程序，并基于Simulink模型仿真對水輪機控制系統進行參數辨識。結果表明，改進矩陣束算法在對水輪機控制系統參數辨識方面是精確快速的。

1 水輪機控制系統模型[8]

水輪機調節系統是由水輪機控制系統和被控制系統組成的閉環系統[8]，結構如圖1所示。

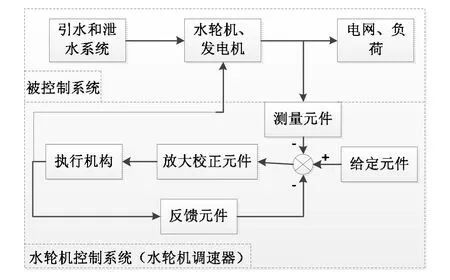
圖1 水輪機調節系統結構框圖

水輪機控制系統由調速器系統和水輪機及其引水系統組成。調速器模型模擬導葉開度的動作情況，以此通過水輪機及其引水系統模型仿真得到輸出功率。

近年來，國內水輪機調速器的主導調節規律多采用以并聯PID為基礎的調節規律，隨動系統采用兩級放大的機械液壓隨動系統，調速器及隨動系統模型框圖如圖2所示。

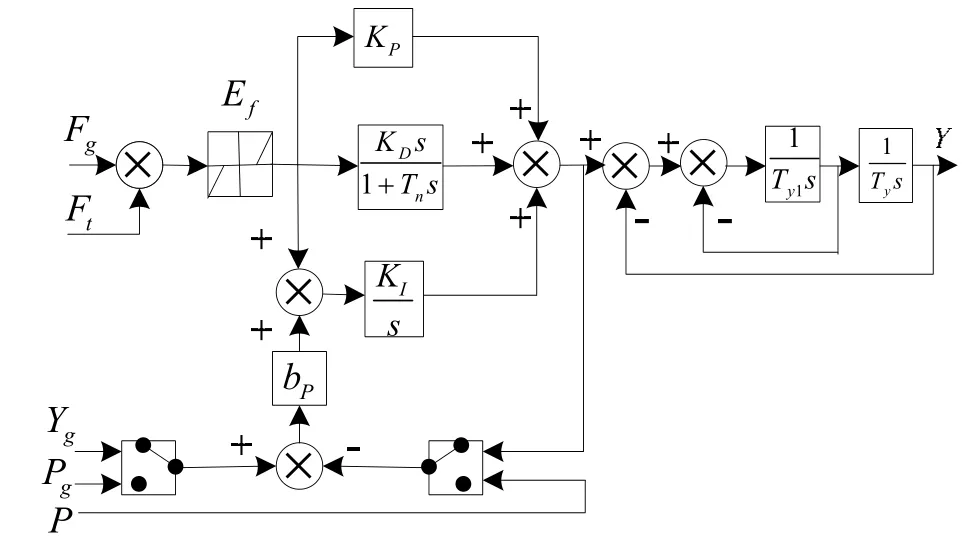
圖2 調速器及隨動系統模型

圖2 中，Fg為頻率給定值；Ft為機組頻率；Yg為開度給定值；Pg為功率給定值；P為機組功率；Ef為人工頻率死區；KP、KI、KD分別為比例、積分、微分增益；bp為永態調差系數；Tn為微分時間常數；Ty為主接力器反應時間常數；Ty1為中間接力器反應時間常數；G為導葉開度輸出。

原動機模型采用簡單水輪機模型，水輪機及其引水系統模型結構框圖如圖3所示。

圖3 水輪機及其引水系統模型

圖3 中，eh，ey分別為水輪機轉矩的水頭傳遞系數和接力器行程傳遞系數，eqh，eqy分別為水輪機流量的水頭傳遞系數和接力器行程傳遞系數，通常取eh=1.5，ey=1.0，eqh=0.5，eqy=1.0；TW為引水系統水流慣性時間常數；mt為功率輸出。

2 基本原理

2.1 矩陣束原理

矩陣束算法可以用于從系統的擾動響應中直接提取與信號有關的信息，如信號的頻率、相位、幅值等[9]。

矩陣束算法采用等間距采樣點，設觀測到的系統響應為y(kΔt)，其離散時間的函數形式為：

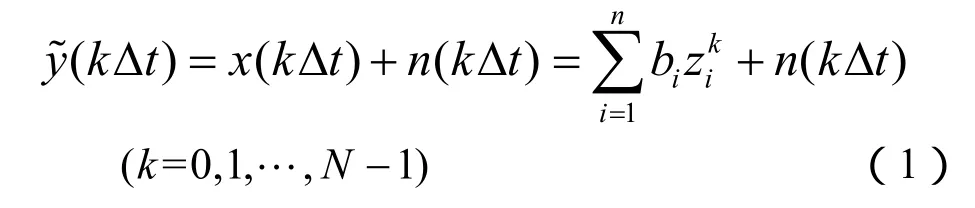
式中：x(kΔt)為不含噪聲的響應；n(kΔt)為系統噪聲；N為采樣點數；Δt為采樣間隔。

將y～(kΔt)作為實際采樣點y(kΔt)的近似。式（1）中，假定bi和zi為復數，即

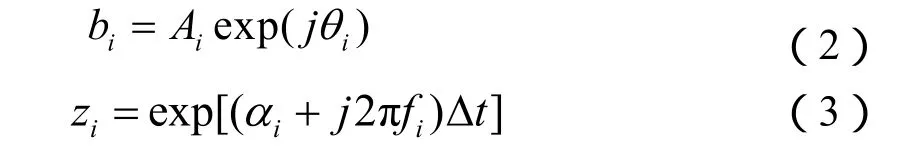
式中：Ai為幅值；θi為相位，rad；αi為衰減因子；fi為振蕩頻率。

步驟1：由采樣序列y(kΔt)構造(N-L)×(L+1)階Hankel矩陣Y，L為矩陣束的參數，恰當的選取L可以有效地抑制噪聲干擾，通常L=N/ 4—N/3。

步驟2：對矩陣Y進行奇異值分解

式中：S為(N-L) × (N-L)的正交矩陣；D為(L+ 1 )×(L+ 1 )的正交矩陣；V為(N-L)×(L+ 1 )的對角陣，其對角元素σi即為Hankel矩陣的第i個奇異值。

對于不含噪聲的信號，Y有L+1個奇異值σi，將其中非零值按下標由小到大構造一個非增序列。從σi中篩選出最大值σmax，若滿足σi/σmax≥μ，則可將最大模態數記為n=i，式中μ為設定的閾值。由V的前n個奇異值形成的新矩陣為

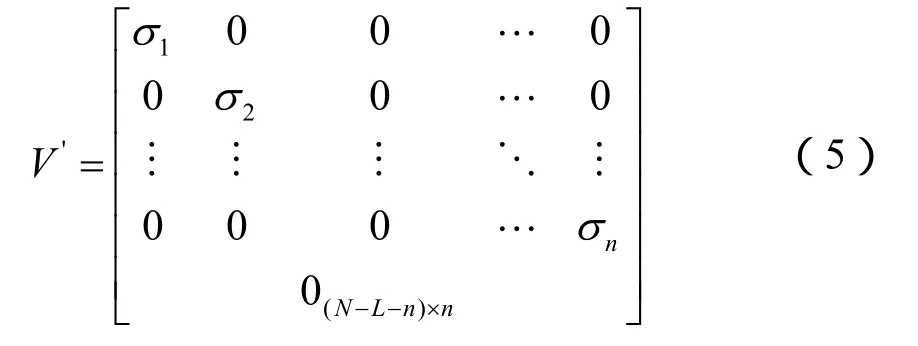
式中，V'為(N-L)×n矩陣，前n行是由Y的前n個非零奇異值組成的n×n方陣，后N-L-n行全為0 。

步驟 3：取矩陣D的前n個主導右特征向量構成(L+1)×n的矩陣D'，刪去D'的最后一行形成L×n的矩陣D1，刪去D'的第一行形成L×n的矩陣D2。定義

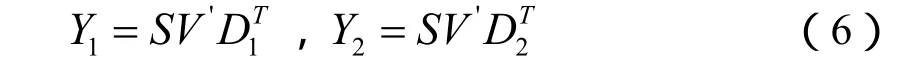
Y1和Y2為2個(N-L)×L階矩陣。

由Y1和Y2組成矩陣束Y2-λY1，并求解其廣義特征值，即求解

式中：為Y1的偽逆矩陣。

矩陣束Y2-λY1的廣義特征值記為λi(i= 1 ,2,3,… ,n)，利用矩陣相關原理可知，此特征值即為采樣信號的極點。

步驟4：根據式（6），可計算得到參數b。

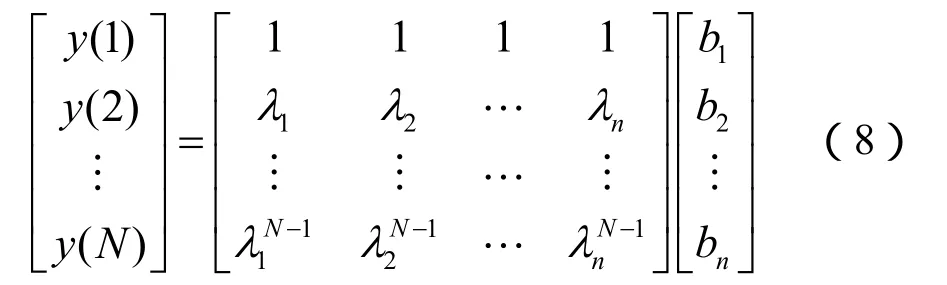
步驟5：利用式（2）、（3）可計算出各分量的幅值、相位、衰減因子和頻率。

2.2 改進的矩陣束算法

Hankel 矩陣Y中的奇異值iσ越小，則所能反映的信息量越少，因此為降低復雜程度，引入信息熵來確定模態階數。將奇異值iσ所占的比重定義為pi，則奇異值的信息熵可以表示為

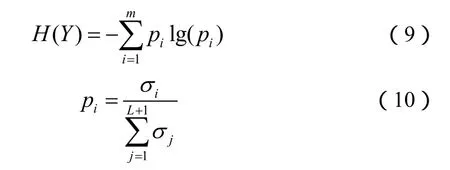
奇異值σi越小，其所占比重pi越小，從而信息熵H(Y)迅速收斂至有界值。當取到奇異值σm時，信息熵H(Y)最接近有界值，此時模態階數可以設定為n=m。

3 基于改進矩陣束算法的參數辨識方法

利用改進矩陣束算法辨識水輪機控制系統參數的步驟如下。

步驟1：對水輪機控制系統模型施加擾動信號，對輸出信號進行采樣。

步驟2：確定改進矩陣束算法中的模態階數。

步驟 3：利用改進矩陣束算法對采樣數據進行運算，確定采樣信號的極點，留數等特征量。

步驟4：利用得到的特征量對調速系統各參數進行辨識。

系統辨識的基本流程如圖4所示。

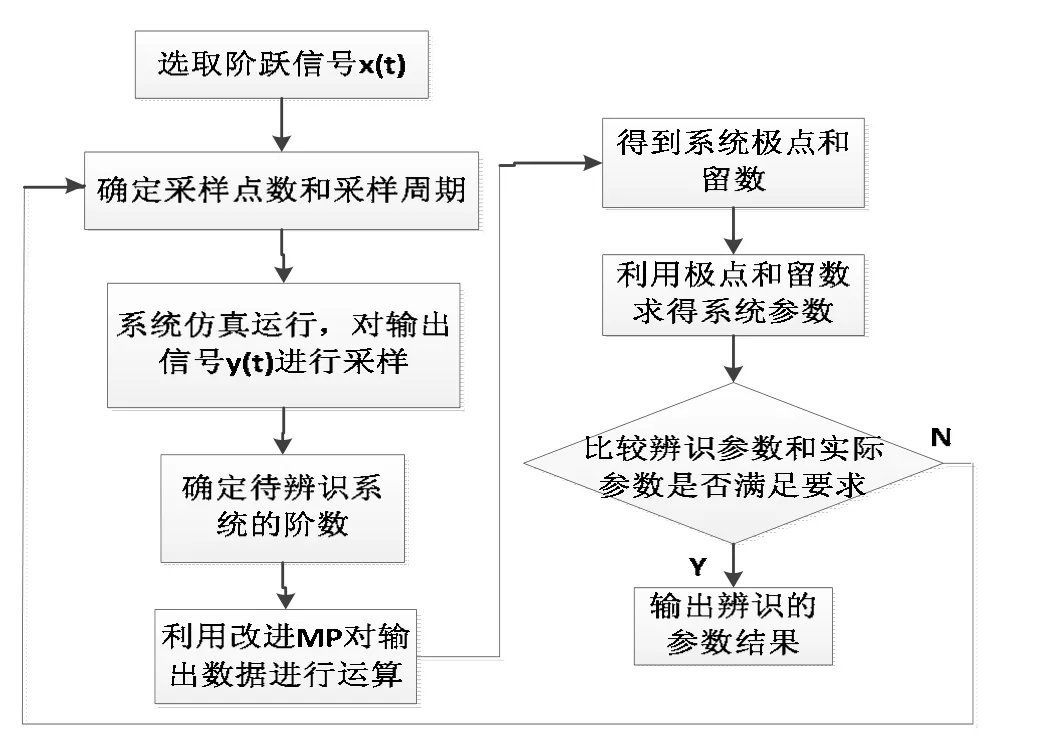
圖4 參數辨識流程圖

4 模型仿真實例

本文通過matlab/simulink建立圖2、圖3所示的水輪機控制系統模型，遵循GB/T9652.1-2007《水輪機控制系統技術條件》、GB/T9652.2-2007《水輪機控制系統試驗規程》的標準，設定調速系統各參數值如下：Ef=0.06%，KP=1.28，KI=0.285，KD=1.25，Tn=0.28s，bp=0.02，Ty=0.65s，Ty1=0.5s，TW=2.0s。水輪機穩定運行于95%出力工況，55s時通過一次調頻使水輪機出力減少 10%，為了驗證改進矩陣束算法對噪聲的抑制能力強及辨識精度高的特點，進行三組對比試驗，其中兩組在輸入信號中加入高斯白噪聲，分別采用改進矩陣束算法和 prony算法對水輪機控制系統參數進行辨識。辨識結果如表1所示。

由表1可知，在加噪聲與不加噪聲兩種情況下，改進矩陣束算法的辨識值均與系統真實值很接近，誤差均在5%以下，表明該方法對干擾具有較強的抑制能力。而同在加噪聲情況下，改進矩陣束算法的辨識精度遠高于prony算法的辨識精度。

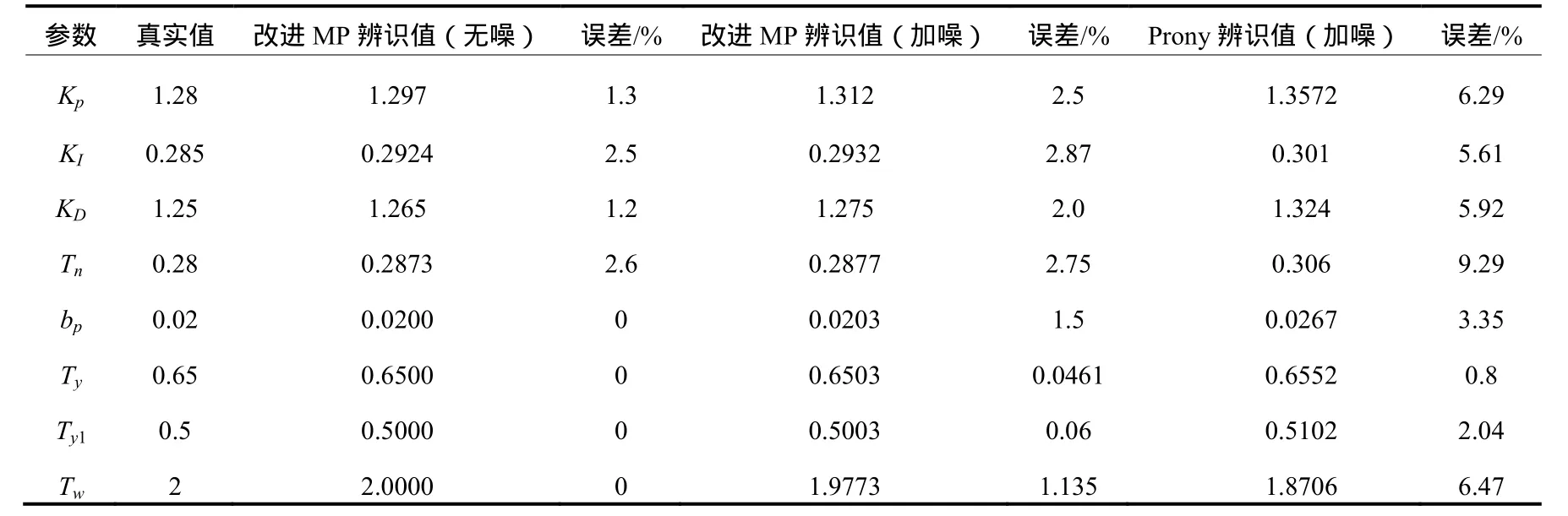
表1 水輪機控制系統參數辨識結果

將表1的三種辨識結果分別代入到模型中進行仿真，導葉開度輸出和功率輸出曲線如圖5和圖6所示，圖中曲線1為實際系統輸出結果，曲線2為理想情況下改進矩陣束算法辨識得到的參數模型的仿真輸出結果，曲線3為加噪聲時改進矩陣束算法辨識得到的參數模型的仿真輸出結果，曲線4為加噪聲時prony算法辨識得到的參數模型的仿真輸出結果。

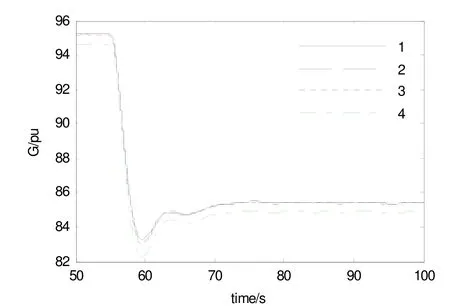
圖5 導葉開度輸出

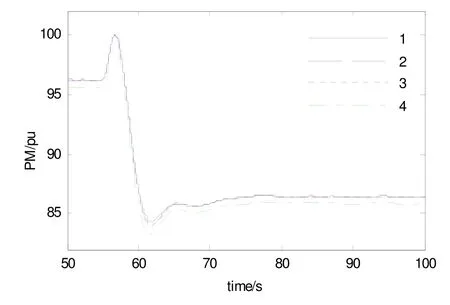
圖6 功率輸出

從圖5和圖6可以看出，系統輸出功率的變化規律與導葉開度的動作情況一致，且曲線2、3與曲線1基本一致，利用改進矩陣束算法得到的辨識模型的仿真輸出曲線與系統的實際輸出曲線基本吻合，模型的整體辨識精度很高，且由曲線3、4的仿真輸出結果可知，改進矩陣束算法在高斯噪聲干擾下的參數辨識結果更貼近實際。

5 結語

改進矩陣束算法利用奇異值分解和矩陣的低秩近似等方法，對噪聲干擾有較強的抑制能力，適合應用于實際工程中，且能較為容易且有效地確定模態階數，提高辨識的效率和精度。

改進矩陣束算法在水輪機控制系統參數辨識方面的應用還是首次，經本文檢驗了其有效性，從而豐富了水輪機控制系統模型參數辨識方法。

[1]龔強, 吳道平．水輪機控制系統參數辨識與系統建模測試簡介[J]．江西電力, 2011, 35(3)：36-39．

[2]李超順, 周建中, 雷慧, 等．基于 Hartley變換的水輪機調速器參數辨識[J]．大電機技術, 2009, 3：57-61．

[3]蘆晶晶, 郭劍, 田芳, 等．基于Prony方法的電力系統振蕩模式分析及PSS參數設計[J]．電網技術，2004, 28(15)：31-34．

[4]劉紅超, 李興源. 基于 Prony辨識的交直流并聯輸電系統直流阻尼控制的研究[J]. 中國電機工程學報, 2002, 22(7)：55-57．

[5]戚軍, 江全元, 曹一家．電力系統傳遞函數的通用Prony辨識算法[J]．中國電機工程學報, 2008,28(28)：41-45．

[6]朱瑞可, 李興源, 趙睿, 等．矩陣束算法在同步電機參數辨識中的應用[J]．電力系統自動化, 2012,36(6)：52-55．

[7]李寬, 李興源, 趙睿, 等．基于改進矩陣束的高壓直流次同步振蕩檢測[J]．電網技術, 2012，36，(4)：28-132．

[8]魏守平．水輪機調節系統仿真[M]．武漢：華中科技大學出版社, 2011．

[9]王宇靜, 于繼來．電力系統振蕩模態的矩陣束辨識法[J]．中國電機工程學報, 2007, 27(19)：12-17．