一個創新型數學實驗項目的設計與實現
□ 呂國才 李 曄 艾冬梅 李艷晴
黨的十八大正式將“創新驅動”上升為國家戰略之后,李克強總理2015年更是倡導要“大眾創業,萬眾創新”。那么,如何實施好創新驅動發展戰略、激發全社會的創新活力、培育經濟社會發展的新動力呢?實際上,高等院校開設的實驗教學就是一門很好的激發學生想象力和創造力的課程,然而由于開設的實驗多以基礎性和驗證性實驗居多,綜合性實驗和創新實驗較少,使得實驗教學沒能完全發揮激發學生創新能力的作用。以數學實驗課為例,近年來,我國許多高等院校都已開設了《數學實驗》課程,并編寫了相應教材[1~4]。然而,許多高校《數學實驗》教學多停留在使用MATLAB等數學軟件,進行一些簡單的驗證性實驗上。這些教學內容對熟悉軟件,初步掌握數學建模的基本方法是有意義的,但是在培養學生創新能力,提高學生的綜合素質方面還很不夠。因此,需要將現有的數學實驗教學提高一個層次[5~7]。將科學研究中一些簡單、有趣的問題移植到創新實驗教學中,有利于調動學生學習的主動性和積極性,激發學生的研究熱情,培養學生創新精神和創新意識。本文精心設計將分子模擬中結構優化的科學研究問題轉化為一個創新實驗教學實驗項目。
隨著計算機技術和數值計算方法的不斷發展,利用計算機模擬技術研究分子的性質已得到廣泛的應用。在模擬的過程中,首先要建立初始模型,由于初始模型的構建通常是靠大量的實測數據的平均值,所以構建出的初始模型不是分子的穩定結構。因此要應用最優化方法對初始模型進行結構優化。這一問題從數學模型建立、求解及最后的結果分析都不是很復雜,可以應用到數學實驗中。數學實驗中常用的最優化方法有單純形法、最速下降法、共軛梯度法和牛頓-拉森方法等[8,9]。共軛梯度法因其存儲小,收斂性好等優點可以用來解決結構優化問題。
一、實驗目的及要求
(一)實驗目的。理解共軛梯度優化方法的基本原理及其優化特點。
(二)實驗要求。掌握共軛梯度方法編程技巧,并能對分子模擬初始模型進行優化。

圖1 Fe原子在三維空間的初始結構
二、實驗原理
共軛梯度法是1952年Hesteness和Stiefel為求解線性方程組提出的,后來用于求解無約束極值問題[10]。它是一種重要的優化方法。共軛梯度法的基本思想是把最速下降法與二次函數共軛方向結合起來,利用已知位置處的梯度構造一組共軛的方向,并沿著這一組方向進行一維搜索,求出目標函數的極小點。
(一)共軛方向的構造。共軛方向可依據Gram-Schmidt正交化方法來構造。設Q是n×n階對稱正定矩陣,g0為任意向量。定義向量序列{gi}和{pi}如下:

取

可使集合{gi}相互正交,集合{pi}是相互Q共軛的。
(二)共軛梯度方法。由式(1)和(2)構成的向量集{pi}是相互Q共軛的,{gi}是相互正交的。當令gi=-△f(xi)時,以下求極值的算法稱為共軛梯度法。
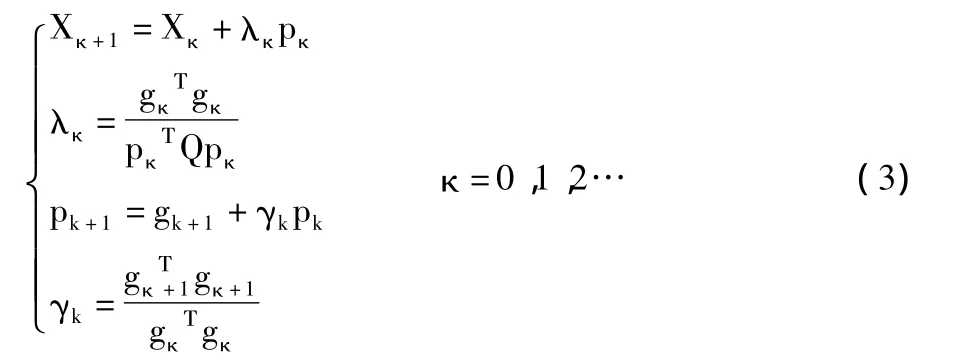
初始值取 x0,p0=g0,= -△f(x0),其中,gκ為 κ點處函數△f(x)的梯度,共軛方向為從κ點開始維搜索的方向。
三、實驗步驟
第一,應用MATLAB軟件構筑Fe原子在三維空間的初始模型,如圖1所示。構筑的x,y和z方向分別沿、和三個晶體學方向。空間點陣大小為10×10×10a0(a0為晶格常數,初始結構的晶常數取3.0)。
第二,應用MATLAB軟件編程實現共軛梯度算法。
第三,用第二步中實現的共軛梯度算法對第一步中構筑的Fe原子初始模型進行結構優化。
第四,實驗數據處理與分析。
四、結果與討論
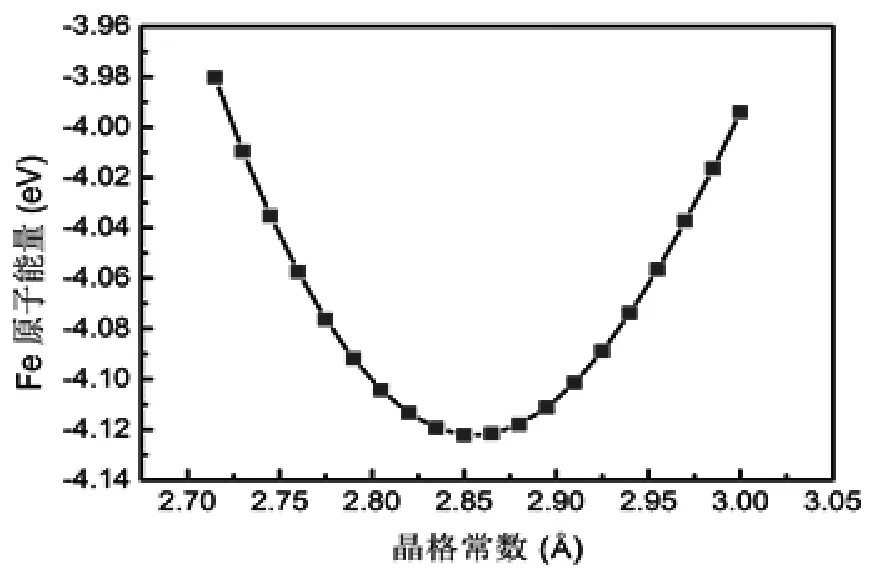
圖2 Fe原子能量與晶格常數間的變化關系
圖2給出的是應用共軛梯算對Fe原子初始結構進行結構優化過程中Fe原子的能量與晶格常數間的變化關系,其中方塊表示能量的數據點,黑色的實線是擬合的曲線。由擬合曲線得到Fe原子的能量在晶常數為2.855時達到最小。因此晶格常數為3.0時的初始結構并不是穩定結構。體系處于穩定結構時的晶格常數應該是2.855。
五、結語
通過上述實驗:可以使學生了解共軛梯度方法的基本原理,掌握應用MATLAB編程的技巧,對于分子模擬結構優化的科學研究問題也有了初步的認識,為學生以后從事科學研究和生產活動打下一定的基礎。同時通過該實驗的實施可將自主創新的科學理念融入到學生的日常學習和實驗中,激發學生探索科學問題的熱情,培養學生的創新意識。
[1]姜啟源,謝金星,邢文訓.大學數學實驗[M].北京:清華大學出版社,2005
[2]艾冬梅,李艷晴,張麗靜.MATLAB與數學實驗[M].北京:機械工業出版社,2014
[3]李秀珍,龐常詞.數學實驗[M].北京:機械工業出版社,2008
[4]王向東,戎海武,文翰.數學實驗[M].北京:高等教育出版社,2004
[5]李繼成,朱旭,王綿森,武忠祥.《數學實驗》課程建設及分層次教學與實踐[J].大學數學,2005,21(6):29~31
[6]周錦蘭,王宏,聶進.多層次大學生創新實驗平臺的構建與實踐[J].實驗技術與管理,2011,28(4):16 ~21
[7]趙冰,阮曉青.新形勢下高等數學分級教學模式的探索[J].高等數學研究,2010,13(5):7 ~9
[8]陳正隆,徐為人,湯立達.分子模擬的理論與實踐[M].北京:化學工業出版社,2007
[9]陳敏伯.計算化學-從理論化學到分子模擬[M].北京:科學出版社,2009
[10]程極泰.最優設計的數學方法[M].北京:國防工業出版社,1981,11

