自動錨泊定位系統的張力混合優化算法

蘇曉宇， 金鴻章， 胡曉東

(1.上海工程技術大學電子電氣工程學院，上海201620;2.哈爾濱工程大學自動化學院，黑龍江哈爾濱150001;3.中船重工第七0四研究所，上海200031)

0 引言

為了改善傳統錨泊定位系統定位精確度低的缺點，本文從經濟性及安全性角度出發，提出一種新的基于錨鏈切換控制的自動錨泊定位方案。該方案為半潛平臺提供均勻分布的水平回復力以平衡環境擾動，以保持其在海面上的位置及安全性。據以往的海洋平臺事故資料，當錨泊事故發生時，首先均是受力最大的錨鏈斷裂，環境外力在余下的纜繩中重新分配又引起余下錨鏈中受力最大的斷裂直至全部斷裂，導致嚴重的后果［1］。因此，環境力在錨鏈上的分配不均是安全的大隱患，有時即使環境載荷不大，但由于受力嚴重不均還是有可能產生事故。所以，研究一種使錨鏈受力均衡的方法尤為必要。所提出的自動錨泊定位方案是以張力的均勻分布為基礎，優化方法的效率和精確度將直接影響整個系統的運行速度和定位精確度，傳統的優化方法則存在各自的局限性，因此利用全局搜索和局部搜索相結合的混合優化策略來提高優化效率，保證海洋平臺的快速準確定位。其中，全局搜索采用遺傳算法，局部搜索則采用模擬退火算法。

由于海洋環境的不確定性，導致系統方程中的水動力參數具有嚴重不確定性，所以采用具有較強魯棒性的保性能控制器來產生抵抗環境擾動的控制合力，其特點是對于所有允許的不確定性，閉環系統是漸近穩定的，并能保證閉環系統的性能指標不超過某個確定的上界［2］。考慮到平臺主要受定常環境擾動的影響，這使得系統的穩態誤差顯著，因此在最優保性能控制器中引入積分作用來減小系統的穩態誤差。

1 自動錨泊定位系統方案

半潛式平臺對于風浪流作用下產生的水平運動不具有回復力，需要配備定位系統以平衡外力。為保證平臺的作業性能及設備安全可靠，提出具有自動收放錨鏈及均衡錨鏈張力分布等功能的自動錨泊定位系統。圖1為系統的原理框圖，系統由積分型最優保性能控制器計算出在環境擾動作用下，平臺定位到期望位置所需要的控制合力，張力優化算法將控制合力均勻分配給12條錨鏈，以保證錨鏈力場的均勻分布，同時將優化值作為錨鏈切換的閾值。隨動機構通過控制錨鏈的收放來保證張力達到設定的閾值，從而使平臺盡可能地保持在海平面上所要求的位置。

傳統的自動錨泊定位系統采用12臺錨機控制12條錨鏈的收放以產生張力來削弱海洋環境的干擾，將其改良為僅由4臺三鏈輪臥式錨機分別對12根錨鏈進行切換控制。中央控制站同時向4臺錨機發送指令，控制4條錨鏈的收放，即每臺錨機的驅動裝置只能與其中的一條錨鏈結合，而其余2條錨鏈處于切斷狀態。當與驅動裝置所接合的錨鏈的張力達到優化方法所設定的閾值時，發送控制指令控制錨機驅動裝置進行切換，與另一條錨鏈接合，繼而控制所接合錨鏈的收放，直到到達理想的位置。這種控制方式在保證平臺的定位精確度的基礎上，降低了自動錨泊定位系統的總體成本，同時兼顧了錨鏈張力場的均勻分布，避免了因張力分配不均而引起錨鏈斷裂的安全隱患。

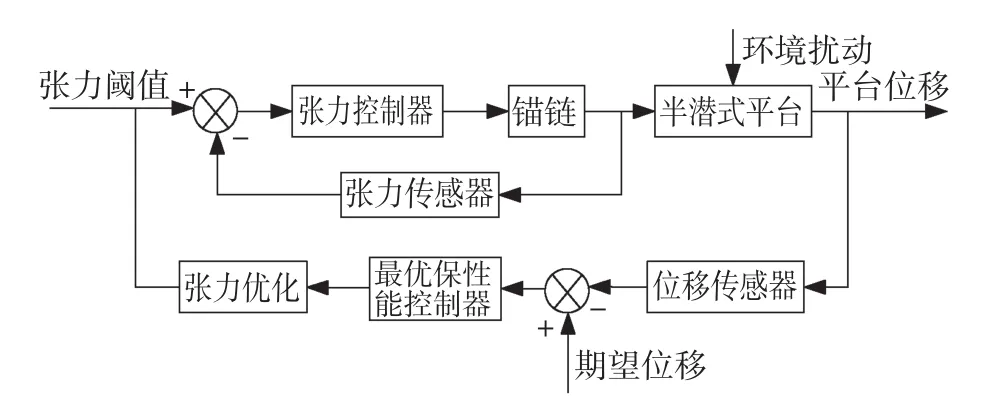
圖1 錨泊自動定位系統原理Fig.1 Principle of Automatic Mooring Positioning System

2 錨泊定位系統保性能控制器設計

2.1 平臺數學模型

半潛式平臺在風浪流等海洋環境擾動作用下將產生高頻往復運動及低頻慢漂運動。高頻運動只是影響到平臺的運動姿態，對平臺位移的影響很小，而低頻運動是使平臺漂離基準位置的主要因素。若對高頻模型進行控制，會引起錨機響應頻繁、錨鏈磨損加速及系統控制能量消耗增加等問題，因此僅考慮平臺的低頻運動模型。平臺水平方向的控制模型一般可表示為

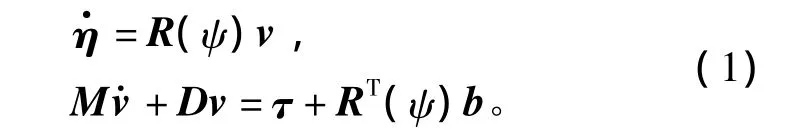
式中:η =［x，y，φ］T為固定坐標系下的平臺縱蕩位移、橫蕩位移及艏搖角度;v=［u，v，r］T為運動坐標系下相應的水平方向上的速度向量;R(ψ)為固定坐標系和運動坐標系間的旋轉矩陣;M為質量矩陣;D為包括錨鏈阻尼及平臺阻尼在內的總阻尼矩陣;τ=［Fx，Fy，Nz］T為錨鏈張力及低頻環境擾動力在水平方向上的合力(力矩);b∈R3表示未建模的環境力(力矩)。為減少旋轉矩陣中的耦合性，假設艏向角相對于期望值的變化不大，則可應用小角理論，非線性的旋轉矩陣可近似的表示為一個單位矩陣［3］:=Rv?Iv，基于此假設條件，式(1)可轉化為如下的狀態空間形式:

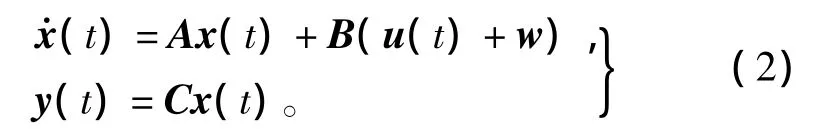
式中:x=［vT，ηT］T為狀態向量，u(t)為水平方向上控制力(力矩)的合力(力矩);W為三維擾動向量，包括穩流風、隸屬于低頻范圍內的湍流風、海流及波浪漂移載荷;y是平臺位置和艏向角的觀測向量。系數矩陣

由于海洋環境的不確定性，使得平臺運動方程中的質量及阻尼矩陣具有嚴重的不確定性［4］，同時考慮到平臺主要受到可視為定常擾動的穩流風，流及二階波浪力作用，使得系統的穩態誤差顯著，因此在模型中引入能有效減小穩態誤差的積分作用形成增廣空間，計入不確定性及積分作用的平臺自動錨泊定位系統控制模型可以表示為

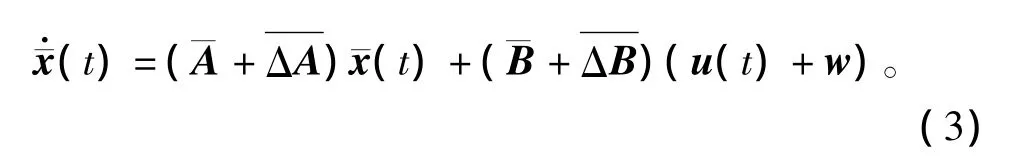
2.2 最優保性能控制

保性能控制是研究不確定系統的一種重要的魯棒控制方法，運用保性能控制可以保證對于所有允許的不確定性，閉環系統是漸進穩定的，并具有一定的魯棒性。針對式(3)所表示的不確定性系統，假設所考慮的參數不確定性是范數有界的，且具有以下形式［5］:

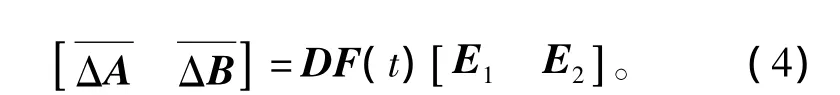
式中:D，E1，E2為適當維數的已知常數矩陣，反應了不確定性的結構信息，F(t)∈Ri×j是一個未知矩陣，它可以是時變的，且滿足:F(t)∈ΩF:={F(t):‖F(t)‖≤I}，針對系統(3)，定義二次型性能指標:

對于系統(3)和性能指標(5)，如果存在一個控制律u(t)和一個正數J*，使得對于所允許的不確定性，閉環系統是漸進穩定的，且閉環系統性能指標滿足J≤J*，則J*為不確定系統(3)的一個性能上界，u(t)為不確定系統的一個保性能控制律。如何選取一個適當的控制律使得系統性能指標最小，即為最優保性能控制，具體過程如下:

定理1 對給定的系統(3)及性能指標(5)，如有以下優化問題:

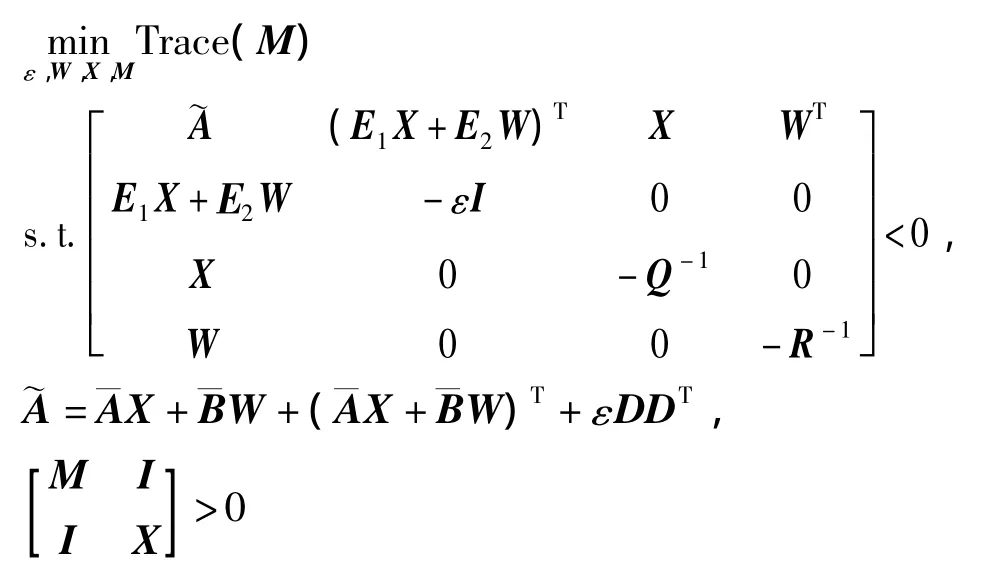
證明過程略，參照參考文獻［5］。

由最優保性能控制計算出使平臺定位到期望位置所需的控制力(力矩)，需張力優化算法將控制合力均勻分配給12條錨鏈，以保證錨鏈力場的均勻分布，同時將優化值作為錨鏈切換的閾值。

3 錨泊定位系統張力優化

3.1 優化模型

錨泊自動定位系統應通過對錨鏈的收放，使平臺盡可能保持在目標位置，并能同時保證各錨泊張力的均勻分布。錨鏈張力的均勻分布對于防止錨鏈斷裂，保證海洋平臺的安全具有重要意義［6－7］。因此，目標是在保證平臺目標位置的基礎上優化錨鏈的張力分布，結合錨泊系統模型，定義目標函數為各錨鏈張力差的平方和，即

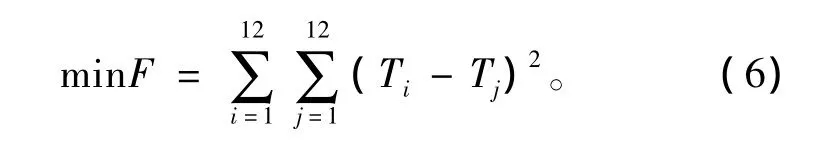
約束條件為

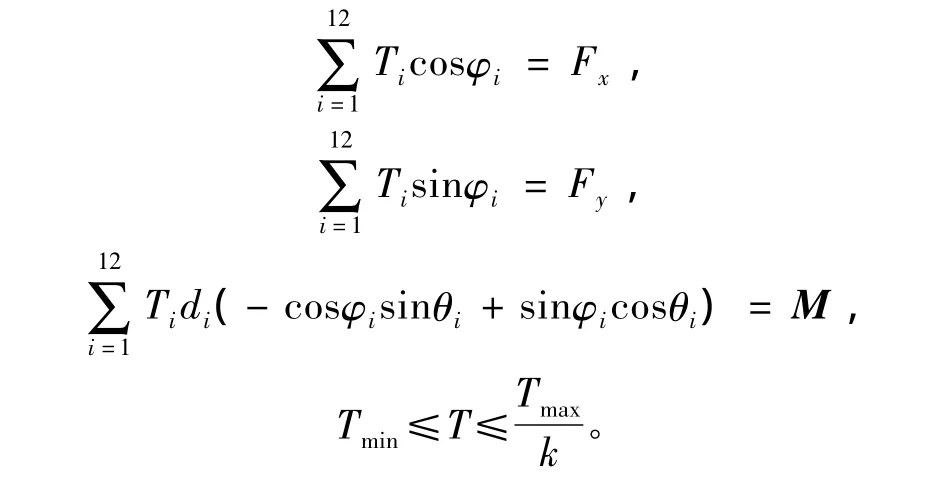
其中:Fx和Fy分別為橫蕩及縱蕩方向上的海洋環境擾動力;M為艏搖方向的海洋干擾力矩;Ti為各錨鏈的張力值;φi為錨鏈的布置角度;θi為著纜點與平臺中心的連線和x軸的夾角;di為著纜點到平臺中心的距離;K是錨鏈的安全因子，根據API RP－2SK規定，其一般大于1.67［8］。約束條件中的等式約束用來保證海洋平臺的位置，而不等式約束則用來保證錨鏈的安全性。

3.2 混合優化算法總體框架

所提出的自動錨泊定位方案是以張力的均勻分布為基礎，優化方法的效率和精確度將直接影響整個系統的運行速度和定位精確度，而傳統的優化方法則存在各自的局限性，因此將遺傳算法和改進的模擬退火算法結合形成混合搜索策略來提高優化效率［9］，保證海洋平臺的快速準確定位。

遺傳算法全局搜索能力強，但進化后期收斂速度慢;而模擬退火算法局部搜索能力強，運行時間較短，求解精確度高。因此，為提高自動錨泊定位系統的整體運行速度，保證錨鏈張力的均衡分布及海洋平臺的定位精確度，借鑒Memetic算法思想將遺傳算法與模擬退火算法相結合。混合優化基本流程的偽碼描述為:

Procedure general MA

begin

for i=1 to p－size do

initialize p(t);

evaluate f(xi);

endfor

if SA is applied then

add the ε largest fitness individuals to EP;

apply SA upon each individual of EP;

endif

do until a termination condition is reached

selection;

crossover;

mutation;

update p(t);

for i=1 to p－size do

update p(t):add EP to p(t)and replace the small fitness individuals with EP;

endfor

select for next generation

enddo

end

其中p－size表示種群個體數，EP表示具有高適應度個體的精英集合。如上面流程所示，這種混合算法仍是從一個隨機產生的初始種群開始，然后利用遺傳算法從種群中選擇適應度較高的精英集合進行局部改進，執行模擬退火算法，直到滿足終止條件為止。

3.3 改進模擬退火算法

模擬退火算法中，隨機搜索變量的產生方式，初始及終止溫度的選取，接受概率及冷卻函數均是影響尋優速度的關鍵因素［10］。在每代進化中引入精英集合EP(‖EP‖?p－size)，僅對EP中的個體進行SA局部搜索。同時對標準SA算法進行改進以提高搜索尋優效率:由混沌遍歷搜索確定初始溫度，以便消除高溫階段的冗余迭代;由一維logistic混沌遍歷搜索代替隨機搜索。用一維logistic映射產生混沌變量，即

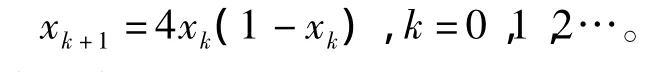
確定初始溫度

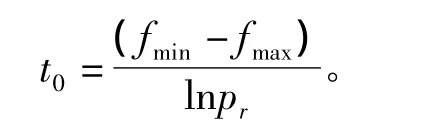
其中:fmin及fmax分別為初始種群中最大及最小適應度值;pr為最差初始接受概率。如此可通過pr來調整初始溫度，避免過高初溫對尋優速率的影響及過低初溫對優化質量的影響。同時用線性變換將logistic產生的混沌向量映射到錨泊線張力分配的狀態空間中，并對其采用混沌遍歷搜索作為SA算法中的搜索策略。

4 仿真結果及分析

對半潛式海洋平臺在一年一遇海洋環境擾動下的縱蕩運動進行仿真研究。為了有效利用Matlab中LMI工具箱，半潛式平臺采用無因次參數描述，在系數矩陣A，B的基礎上，由于積分作用的引入，需對系數矩陣進行增廣，增廣之后如考慮3自由度運動，則系數矩陣A是9維方陣，為節約篇幅，僅給出縱蕩運動設計過程參數，其他兩個自由度具有相同的過程。

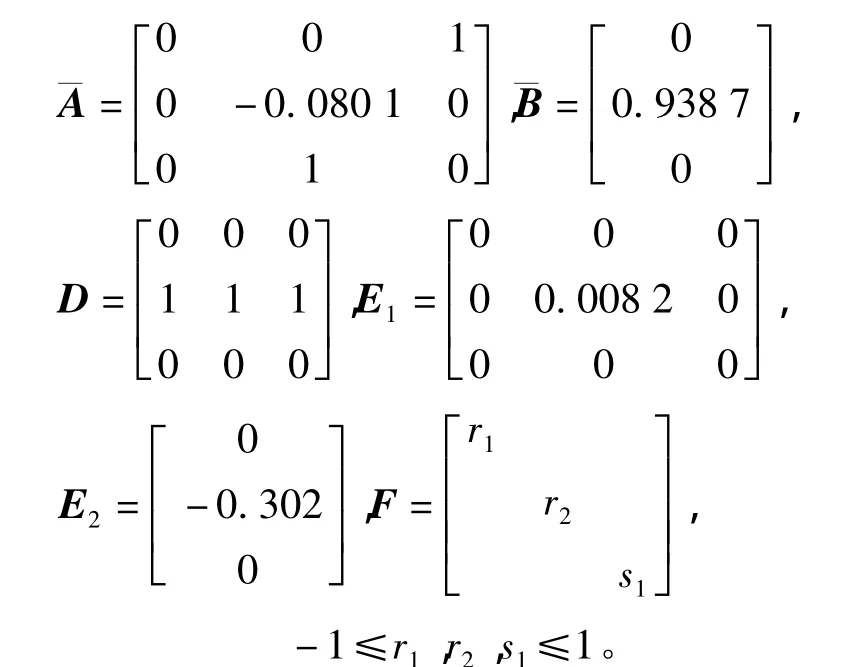
系統性能指標(5)的加權矩陣為

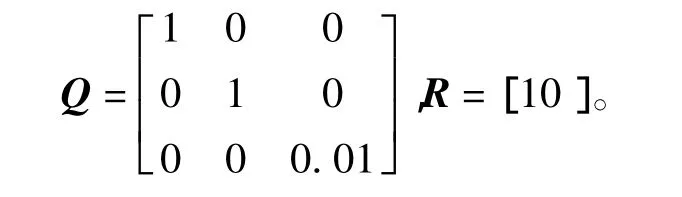
根據定理1，求解矩陣不等式，可得

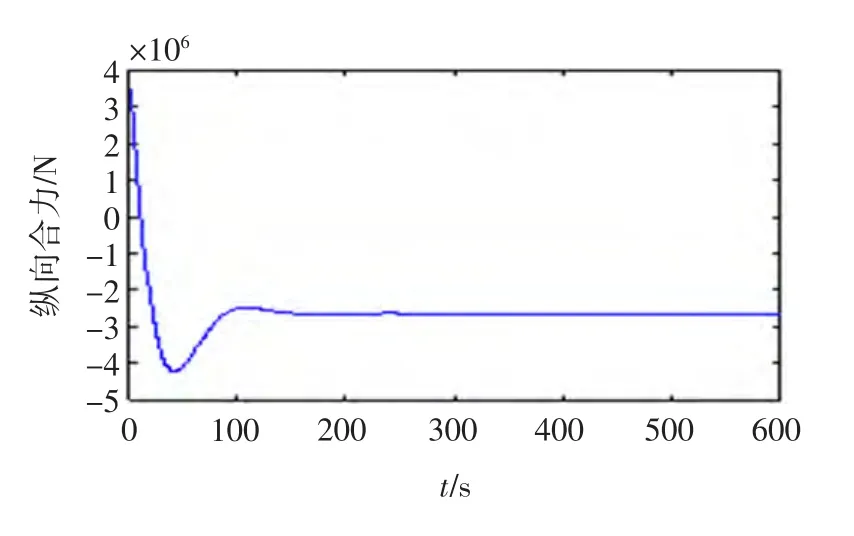
圖2 縱蕩方向的合力Fig.2 Force in surge direction

目標平臺的作業水深為1 500 m，錨泊系統采用鏈－纜－鏈分段組合形式，共12根，布置方式如圖3所示。考慮風、浪、流方向相同的最不利工況(以海洋環境載荷以45°方向作用于平臺為例)。

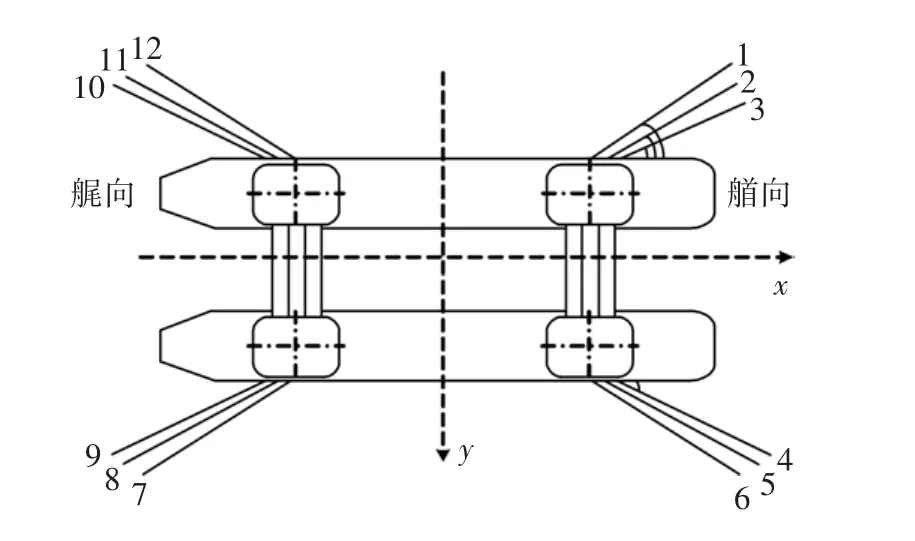
圖3 錨鏈布置示意Fig.3 Distribution of mooring lines

令初始種群規模為200，在遺傳算法的選擇操作中應用精英保留策略，即通過適應度函數對個體進行評價排序，適應度較高的個體(本文中選取20%)進行局部改進，執行模擬退火算法。遺傳算法交叉概率0.7，變異概率0.02，精英保留個數40，進化代數200。模擬退火算法中初始溫度500℃，溫度下降參數0.85。分別采用遺傳算法及混合優化算法對12根錨鏈的張力分配進行優化。優化結果如表1及圖4所示。

優化結果表明，混合優化算法相對于傳統遺傳算法更適合于本文提出的基于錨鏈張力優化值作為切換閾值的海洋平臺自動錨泊定位系統的設計，因為其具有更快的收斂速度及更高的優化精度，能夠保證海洋平臺的快速準確定位，平臺縱蕩方向的位移如圖5所示。

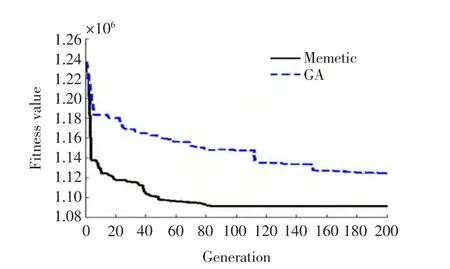
圖4 兩種優化方法進化進程Fig.4 Evolution process of two optimization methods

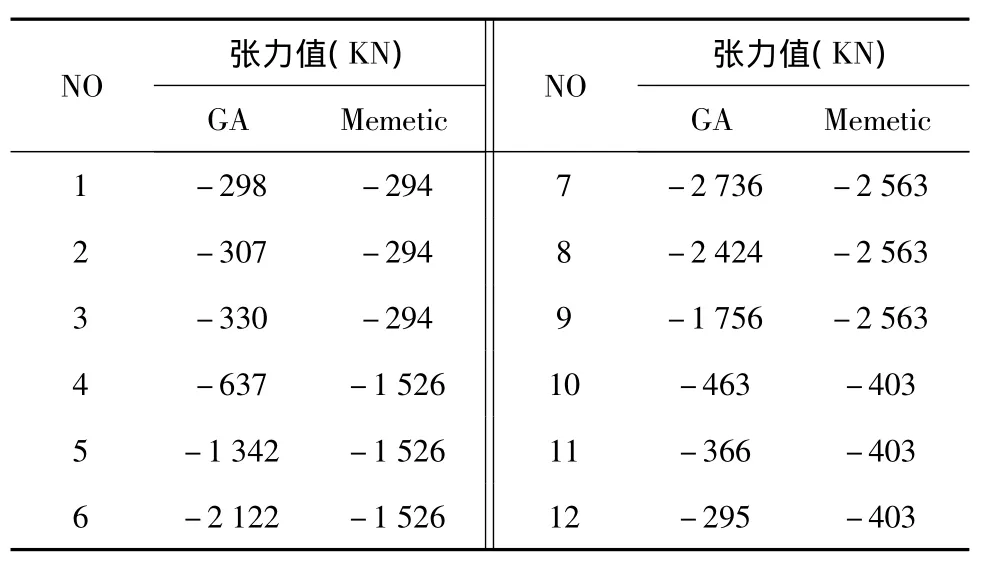
表1 兩種優化方法優化結果Table 1 Optimization results of two methods

圖5 平臺縱蕩位置仿真結果Fig.5 Surge simulation results of the platform

由圖可知，引入積分作用的最優保性能控制有效減小了穩態誤差。但引入積分作用后，仍存在一定的穩態誤差(期望位置為縱向5 m處)，一方面是由于作為錨鏈切換閾值的張力優化結果存在一定的允許誤差，致使張力的合力不恒等于零而引起的位移偏差;另一方面，環境擾動中的高頻一階干擾力所引起的誤差:為了避免錨機動作頻繁，錨鏈的磨損加速及控制能量消耗增加等現象，僅對低頻擾動進行控制，盡管控制過程中不計入高頻的一階干擾力，但其作為環境擾動是真實存在的，在理想情況下，高頻一階擾動是均值為零的隨機過程，但在一段時間內，其均值存在不等于零的情況，引起一起部分誤差。雖然方案存在一定的誤差，但其充分滿足平臺的作業要求，并能均衡錨鏈力場的分布，保證了海洋平臺工作的安全性。

5 結論

本文提出了一種基于錨鏈切換控制的自動錨泊定位新方案。利用保性能控制在處理參數不確定性方面的優勢，設計了改進最優保性能控制算法，解決了由于海洋平臺運動模型的不確定性對系統設計造成的困難，同時所設計的控制器由于積分作用的引入，減小了系統的穩態誤差。張力優化方面，利用遺傳算法和模擬退火算法的互補性，以實現各錨鏈張力值方差最小為目標函數，構造混合算法來優化錨鏈的張力分布以使其受力均衡，防止單根錨鏈因受力過大而斷裂，并將優化結果作為錨鏈切換的閾值。優化結果表明，混合優化算法具有更快的收斂速度及更高的優化精確度，更加適用于本系統設計。整體仿真表明，提出的方案能夠保證海洋平臺的定位要求，并能兼顧錨鏈力場的均勻分布。同時，由于錨鏈切換控制的加入，使得該錨泊定位系統僅采用4臺三鏈輪錨機即可實現原有12臺錨機的功能，降低了系統的總體成本，保證了經濟性。

［1］BERNTSEN P I，LEIRA B J.Ensuring mooring line integrity by dynamic positioning:Controller design and experimental tests［J］.Automatica，2009，1285 －1290.

［2］馬闖，李清華，伊國興，等.大延時網絡化控制系統保性能控制［J］.電機與控制學報，2008，12(1):104 －108.MA Chuang，LI Qinghua，YI Guoxing，et al.Guaranteed cost control for networked control systems with large time delays［J］.Electric Machines and Control，2008，12(1):104 －108.

［3］GARRETT D.Coupled analysis of floating production systems［J］.Ocean Engineering:2005，32(7):802－816.

［4］SORENSEN A.Structural issues in the design and operation of marine control systems［J］.Annual Reviews in Control，2005，29(1):125－149.

［5］俞立.魯棒控制——線性矩陣不等式處理方法［M］.北京:清華大學出版社，

［6］LOTFI K G，SHERIFA M，ASHRAF O N.A particle swarmbased genetic algorithm for scheduling in an agile environment［J］.Computers＆ Industrial Engineering，2008，55(3):707－720.

［7］SHAFIEEFAR M，REEZVANI A.Mooring optimization of floating platforms using a genetic algorithm［J］.Ocean Engineering，2007，34:1413－1421.

［8］嚴傳續，錢宏，項軍毅，等.鋪管船錨泊定位系統優化設計研究［J］.中國造船，2010，51(1):84 －93.YAN Chuanxu，QIAN Hong，XIANG Junyi，et al.Study on design optimization of mooring positioning system for pipelaying vessel［J］.Shipbuilding of China，2010，51(1):84 －93.

［9］GALLARDO J E，COTTA C，FERANDEZ A J.On the hybridization of memetic algorithms with branch-and-bound techniques［J］.IEEE Transactions on Systems，Man，and Cybernetics－ Part B，2007，37(1):77－83.

［10］張軍，張侃諭，周強.基于改進模擬退火算法的多臺冷水機組負荷優化分配［J］.農業機械學報，2012，43(3):187－19.ZHANG Jun，ZHANG Kanyu，ZHOU Qiang.Improved simulated annealing algorithm in optimal load distribution of multiple chillers for energy conservation［J］.Journal of Agricultural Machinery，2012，43(3):187－19.