立體幾何課堂教學中模型應用的思考和探索

邵鵬菲

立體幾何是高中數學較有特色的一個部分，是學生第一次較為系統和全面地學習三維空間的知識，不僅是對初中所學的平面幾何的延伸，也是為他們今后進一步學習高等數學打下基礎，這部分內容在高考中也占有一定的比重，因此教師在進行這部分的教學時較為細致。其中“異面直線所成角”這一小節內容是高中數學教學要求中明確文理科都必須掌握的，可謂是重中之重。

在我初次接觸立體幾何教學時，我注意到教材中在介紹了異面直線所成角的定義之后，給出了下面這個非常基礎的例題：

【例】已知正方體ABCD-A1B1C1D1的棱長為a，求下列異面直線所成角的大小：

（1）AB與B1C1；（2）A1B與CC1；（3）AB1與BC1

作為如此重要的一個教學內容，當時的我覺得僅給出這樣一個例題太過簡單。正方體是學生較為熟悉的一種幾何體，也是比較特殊的幾何體，即使學生會在正方體中求異面直線所成角，那在其他幾何體中，他們是否還會呢？何況在配套的練習中，的確出現了很多在普通棱柱、棱錐中求異面直線所成角的習題。于是，我在教學過程中，添加了兩道例題：

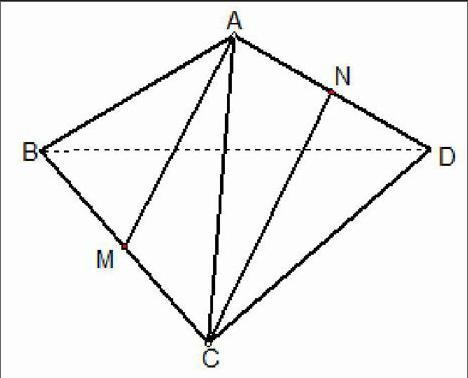
【補1】空間四邊形ABCD中，AB=BC=CD=DA=AC=BD=a，M、N分別是BC、AD的中點，求AM與CN所成角的大小。（平移法）

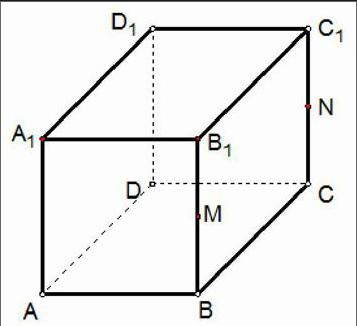
【補2】長方體ABCD-A1B1C1D1中，AB=5，BC=3，AA1=4，求AC與BD1所成角的大小。（補形法）

經過實踐發現這樣的課堂效果并不理想，主要有這樣一些問題：

1.學生接觸立體幾何時間還不長，對于用平面圖像表現空間幾何體還未完全接受，因此，識圖和繪圖有困難，每道題出現，他們要花很多時間來畫圖，添加輔助線時更是不知所措，經常是畫平行線卻畫出異面直線；

2.整節課時間非常緊張，學生能夠自主思考的時間非常少，基本上是聽老師不停地提示和引導，就算是這樣緊湊的情況下，補2還沒能講完；

3.三道例題需要畫出三種不同的圖像，其中還蘊含兩種解題方法。上課時就發現有些學生皺著眉頭，有些學生一臉茫然，只顧著模仿我的作圖和抄寫筆記。學生反饋說感覺就是一會兒這樣一會兒那樣，即使跟著老師的引導，也會覺得比較累。

出現了這樣的情況，讓我意識到這節課內容的教學活動不能一味加大例題的容量，而應從根本上先排除學習障礙——圖像。我回憶了我自己在學習立體幾何時的經歷：那時候我作為學生，對于立體圖像也不是一下子適應的，于是我每天會有一些時間用在制作模型上，遇到難以理解的圖像，就根據題意用細鉛絲和老虎鉗做個實物拿在手上觀察，用細繩綁在模型上表示各種異面直線，久而久之，我能夠自如地畫出各種立體圖像，熟練地判斷空間各種關系，也不再覺得添加輔助線是很難預知的事情了。

在第二天的教學中，我帶去了兩個相同的長方體模型。當我拿著模型出現在講臺上時，學生都很新奇地看著這個東西，瞬間注意力集中到了課堂上。為了將前一天未講完的補2分析清楚，我配合例題在模型上用彩色的塑料繩分別表示出了異面直線，讓學生很直觀地看到了它們的位置。因為要講的是補形法，我便將兩個長方體拼接起來，幾乎就是在那一瞬，他們看出了異面直線所成角的位置。

課后竟然有學生跑上講臺主動要求看那個模型，他們覺得看著模型就能夠理解圖像中的實線和虛線分別表示了哪些線條，摸到看到實物后，就很容易聯想到需要添加哪些輔助線。同時他們表示，可惜上課時只有老師手里有模型，他們只能下課后來摸一摸。我很高興曾經幫助過我的模型在多年后也能幫到我的學生們，于是鼓勵學生們自己嘗試做一些模型。這之后，在立體幾何的學習過程中，圖像對他們來說不再那么難以接受，輔助線也不再那么“高深莫測”。

時間飛逝，一轉眼我第二次接觸到了立體幾何這一章的教學。雖然在第一次教學中，我及時用模型補救，幫助學生克服了圖像的障礙，可是那節課呈現出的其他問題不止一次地引起我的反思。

隨著不斷地學習和進修，我的教學理念也發生了一些變化，我開始認識到數學課堂教學應該是活動的教學，教師的作用是引導學生進行數學活動，倡導的數學學習方式是自主探索、合作交流與動手實踐。而且在校本培訓中，前輩們不止一次地提到過，我們不是要將所有的題目呈獻給學生，而是要教會他們自己思考和總結方法，正所謂“授人以魚不如授人以漁”。所以我想在這次教學中嘗試新的模式，不僅解決圖像的問題，也要盡量增加學生的思考空間。既然上次題量過大導致學生無暇思考，那這次我就精簡例題，以期事半功倍。

我事先利用課余時間組織學生用一次性吸管做了很多正方體模型，基本上全班可以保證每兩人至少有一個模型。而上課時，我先用動畫課件解釋了異面直線所成角的定義和原理，然后給出了唯一的例題：

【例】已知正方體ABCD-A1B1C1D1的棱長為a，M、N分別是BB1、CC1的中點，求下列異面直線所成角的大小：

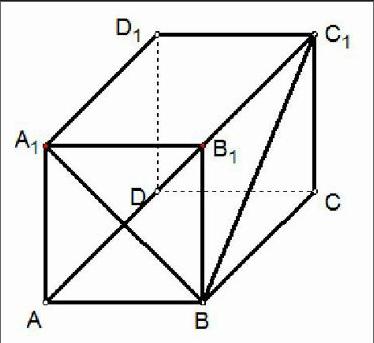
（1）AB與B1C1；（2）AB1與CC1；（3）AB1與BC1；（4）AM與BN；（5）AC與BD1

前三個小題是書上的原題，比較基礎，常規方法（平移法）足以解決，所以我決定完全由學生自己看著模型思考，我只是根據他們的描述簡單寫了較為規范的解題過程，提醒他們如何將思路用數學語言表達清楚。

第四小題稍有變化，我建議他們兩人一組討論。一陣沉默之后，他們一人扶著模型，一人拿著塑料繩比劃。過了沒多久，有人叫著“這兩條不是平行線嘛，這不就平移到一個交點了嘛！”“我找到這條了！”……我笑著請幾位學生分別介紹他們找到的平行線，雖然線各不相同，但是答案卻不謀而合，真正是“英雄所見略同”。

第五小題是思考題，是“借用”了之前的補2，我建議他們四人一組討論。與之前大不相同的是，這次時間上很充足。有的學生還是在努力比劃著平行線，想模仿之前的小題用平移法解決問題，而有的學生看到自己有不止一個模型，便考慮將兩個模型拼接起來，這樣一來他們竟然在沒有得到任何提示的情況下，自己找到了補形法！我順利地“教”會了他們這兩種方法：平移法和補形法。

之后作業反饋的情況也非常理想，學生并沒有像我最初想象的那樣，被局限在正方體中，而是在其他圖形中仍然應對自如。

按照烏申斯基的說法，直觀的教學不是以抽象的概念和詞語為依據，而是以學生的直接感知的具體形式為依據的。因此，教會學生去有意識地使用立體幾何模型，是順利地進入立體幾何之門的金鑰匙。而且模型并不局限于教學使用的立體幾何教具，也可以是學生觸手可及的桌面、書本、筆等。善于使用這些現成的模型，可以使許多立體幾何問題變得比較直觀，比較容易解決。

立體幾何的教學，還要能調動學生的學習興趣，幫助他們建立學習的自信，讓他們找到“竅門”，學會空間與平面之間的聯想與轉化。其實立體幾何的許多定理、結論都源自生活實際，源自平面幾何，因此要教會學生聯想實際模型，聯想平面幾何中已經熟悉的東西，借助可取之材來建立空間想象，其中若能加強直觀教學，就容易讓學生接受，讓他們喜歡上這一門學科，從而更有效地培養他們的空間想象力，提高他們解決立體幾何問題的能力。

這樣看來，動手制作模具的活動不僅能幫助學生具體直觀地理解空間幾何體，還讓學生對這部分“陌生”的知識產生了興趣和學習的信心，從而培養學生的自主設計、自主探索、自主歸納和總結的能力。雖然制作與畫圖過程都需要花費一定的時間，但只要教師作適時、必要的引導，課堂適當采用多媒體配合使用，發揮各自優勢，互補各自不足，還是可以獲得意外的收獲的。

（作者單位：上海風華中學）endprint