法線和副法線螺旋彈簧勁度系數的研究

戴璐，臧濤成，葛麗娟

（蘇州科技學院數理學院，江蘇蘇州215009）

法線和副法線螺旋彈簧勁度系數的研究

戴璐，臧濤成，葛麗娟

（蘇州科技學院數理學院，江蘇蘇州215009）

借助于Cosserat曲線理論定量研究了法線和副法線螺旋彈簧的勁度系數。計算結果表明，在拉伸螺旋彈簧過程中勁度系數并非始終保持定值。并且副法線螺旋彈簧比法線螺旋彈簧有更好的線性彈性性，所以副法線螺旋彈簧更有利于應用在機械系統。

法線和副法線螺旋彈簧；Cosserat曲線理論；勁度系數

在大學物理的教學研究中彈簧的勁度系數被認為是常數[1-2]。然而筆者在研究微納米螺旋機械性質的時候發現，螺旋結構的胡克常量會隨著螺旋軸向拉伸而變化[3]。微納米螺旋具有超彈性，其在軸向高負載的作用下幾乎可以被拉伸成直線，當撤去負載時，螺旋恢復原形，所以微納米螺旋可以被當作彈簧[4-5]。筆者將借助考慮了拉伸和剪切形變的Cosserat曲線建立一套理論來定量研究整個拉伸和拉斷區域法線和副法線螺旋彈簧的勁度系數。

1 Cosserat曲線理論

Cosserat曲線這一概念首先在1909年由E·Cosserat和F·Cosserat提出，他們用3個方向矢量來定義一條曲線，并用4個矢量場來表示該曲線，即Cosserat曲線[6]。Whitman和DeSilva將該理論應用于彈性細桿的研究，從而形成彈性細桿三維非線性平衡理論，即彈性細桿的Cosserat曲線理論[7-8]，其平衡方程為

其中τ，m分別為作用于整個細桿的力和力矩矢量，ε為輪轉算符，W和y分別為位置矢量和方向矢量。下標α，β，γ取1，2，3。，拉伸量λ＝?s/?S，S和s分別為沿著固定結構和形變結構的弧長。

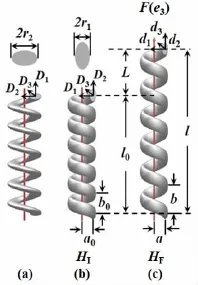
圖1 法線螺旋彈簧結構（a）及副法線螺旋彈簧受到軸向拉力F作用前后的結構（b）、（c）

如圖1（a-c）所示，筆者考慮了兩種橢圓截面的螺旋形彈簧，分別稱為法線螺旋和副法線螺旋[9-10]。橢圓截面的兩個半軸長分別為r1和r2（r2＞r1）。假設一N匝均勻螺旋HI，半徑為a0，螺距為b0，長為l0。螺旋HI在軸向拉力F作用下被拉伸為螺旋HF，半徑為a，螺距為b，螺旋拉伸量為L。在模型中HI為Cosserat曲線理論中固定參考結構，而HF為形變結構。Di（i=1，2，3）為螺旋HI的方向基矢，而di為螺旋HF的方向基矢，它們分別由兩組歐拉角φ0，θ0，ψ0和 φ，θ，ψ定義。對于螺旋結構都為常數，不隨弧長變化[11]。選擇HI的第三個方向矢量D3沿著螺旋線中心線的切向，拉力F沿著固定笛卡爾坐標系的e3軸。D1、d1和D2、d2分別沿著彎曲剛度最大和最小的方向。

法線螺旋和副法線螺旋HI的方向變化矢量W（0）有以下形式

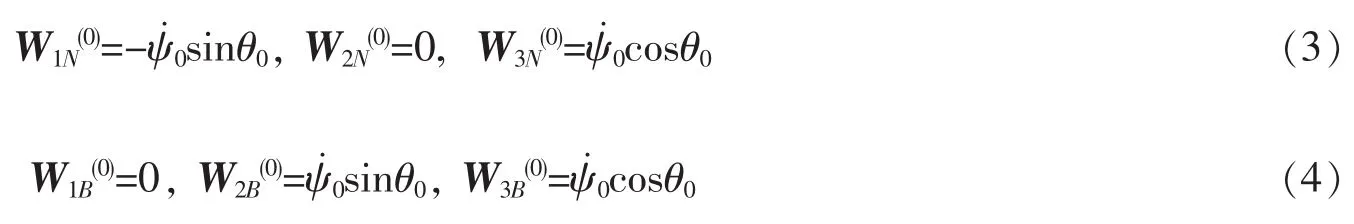
將螺旋HF的方向變化矢量代入平衡方程（2）得到法線螺旋的方程

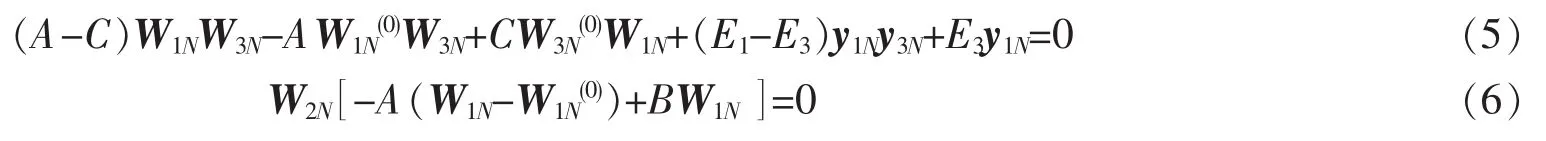
和副法線螺旋的方程

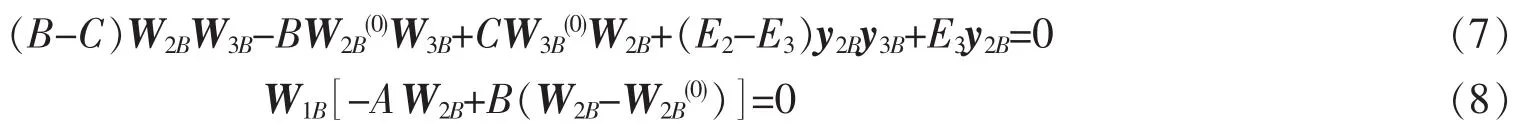
其中E1=E2=KGtw，E3=Etw，A=EI1，B=EI2和C=4GI1I2/（I1+I2）[12]。K為Timoshenko切系數，可用泊松比ν來表示[12]。E和G=E/2（1+ν）分別是楊氏模量和切模量。I1=（πr23r1）/4和I2=（πr2r13）/4是截面的轉動慣量。

因為負載力決定了螺旋HF的形狀，所以方程（6）和（8）表示，對于法線螺旋來說方向變化矢量W有如下形式

對于副法線來說W有如下形式

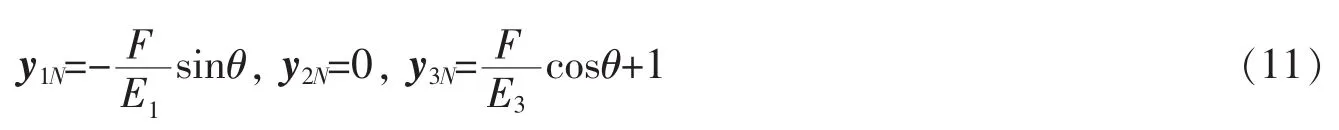
以及副法線螺旋的變化矢量

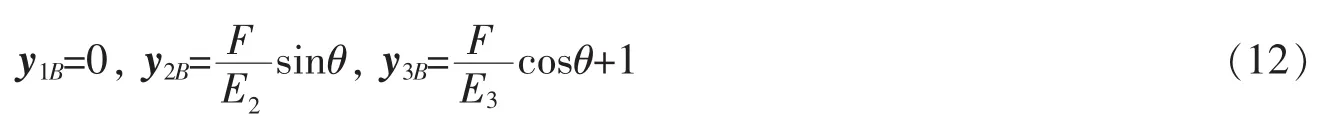
根據方程（11）、（12），不僅可以得到拉伸量λ

還能得到法線和副法線螺旋HI和HF的半徑和螺旋角，用歐拉角表示為

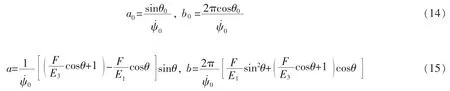
其中Δ≡I2/I1，對于法線（或者副法線）螺旋來說i=1（或者i=2），δi2為克羅內克函數。并且力矩M沿著螺旋軸向，即負載力F方向的表達式為

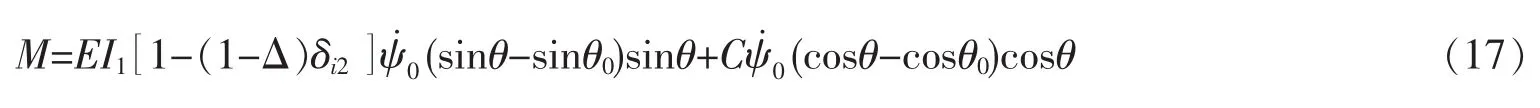
根據方程（14）、（15）、（16）和胡克定律k=dF/dL，螺旋HF的勁度系數可表示為

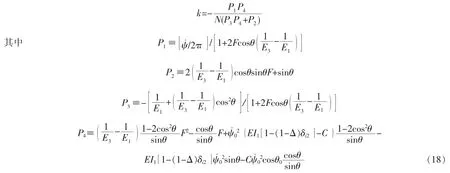
通過測量螺旋HI的幾何參數a0，b0，r1，r2，N和負載或者力矩，就可以根據方程（13-18）以及螺旋線長度l=λl0和體積守恒條件分別是螺旋線形變前后的長度（如圖1（a）和1（b）））來計算螺旋HF的半徑a，螺距b和勁度系數k。

2 討論與結果

筆者將基于Cosserat曲線模型，利用Si3N4微米螺旋來定量研究在整個軸向拉伸過程中法線和副法線螺旋的勁度系數。Si3N4微米螺旋具有圓截面，其半徑為r0=2.58 μm[5]。在計算中假設螺旋線截面面積為定值πr02，然后令長短半軸比為2來得到橢圓截面螺旋。Si3N4微米螺旋的其他幾何參數和材料參數為a0=80 μm，b0=200 μm，N=8，E=240 GPa[5]，ν=0.25[13]，其中幾何參量來自于SEM圖像。首先要確定螺旋能承受的最大負載，即拉斷螺旋的力Fbreak。根據楊氏模量和勁度系數的定義，在拉斷點有k=kS=EA/l0，其中kS為螺旋線彈性常數，A為拉伸后螺旋線截面面積（A=πr1r2/λ）。結合方程（14）-（18），得到Si3N4微米法線和副法線螺旋能承受的最大負載分別為Fbreak=120×10-3N和Fbreak=51×10-3N。

在已知材料的Fbreak后，根據方程（18）圖2（a）和2（b）分別給出了整個拉伸區域Si3N4法線和副法線微米螺旋的勁度系數。勁度系數—拉伸曲線可分為3個區域：區域I為螺旋線性彈性區域。在該區域內，即負載初始階段，勁度系數幾乎不隨伸長變化，法線螺旋平均值為0.39 N·m-1，副法線螺旋的平均值為0.28 N·m-1。區域II為螺旋非線性彈性區域。在該區域中繼續拉伸螺旋，螺旋被拉緊，勁度系數呈非線性增長到高應力區域：勁度系數隨拉伸迅速增加。區域III為螺旋線線性彈性區域，在該區域螺旋被更大負載力拉成一根緊繃直線直到拉斷，其勁度系數進入一飽和值，即螺旋線彈性常數kS。

通過比較圖2（a）和2（b）可以得到法線和副法線螺旋的線性彈性區域分別為大約1.2 mm和2.1 mm處，這兩個螺旋拉伸量分別為螺旋原長的600%和1 050%。顯然副法線螺旋的線性彈性區域更大，這表明副法線螺旋的線性彈性性更好，也就是機械穩定性強。并且在線性彈性區域內副法線螺旋的勁度系數比法線螺旋的勁度系數小，在相等的負載力作用下，副法線螺旋會有更大的形變量，即彈性更好。所以副法線螺旋更有利于應用在機械系統。

3 結語

基于Cosserat曲線理論定量研究了大學物理中彈簧的勁度系數。以橢圓截面法線和副法線螺旋彈簧為研究對象，推導出以螺旋幾何參數、材料參數和負載力為自變量的勁度系數表達式，并利用Si3N4微米螺旋彈簧定量解釋了整個拉伸和拉斷區域的勁度系數。研究結果發現，在拉伸過程中螺旋彈簧的勁度系數會發生變化，而副法線螺旋彈簧比法線螺旋彈簧有更長的線性彈性性區域，因此，更有利于應用。

[1]馬文蔚，周雨青.物理學教程（上冊）[M].2版.北京：高等教育出版社，1999.

[2]程守洙，江之永.普通物理學（上冊）[M].6版.北京：高等教育出版社，2006.

[3]Dai L，Shen W Z.Cosserat curve model for superelasticity of helices[J].Nanotechnology，2009，20（46）：465707（1-6）.

[4]Chen X，Zhang S，Dikin D A，et al.Mechanics of a carbon nanocoil[J].Nano Lett，2003，3（9）：1299-1304.

[5]Cao C B，Du H L，Xu Y J，et al.Superelastic and spring properties of Si3N4microcoils[J].Adv Mater，2008，20（9）：1738-1743.

[6]Cosserat E，Cosserat F.Theorie des Corps Deformables[M].Paris：Hermann，1909.

[7]Whitman A B，DeSilva C N.Stability in a linear theory of elastic rods[J].Acta Mechanica，1972，15（3、4）：295-308.

[8]Whitman A B，DeSilva C N.An exact solution in a nonlinear theory of rods[J].J Elasticity，1974，4（4）：265-280.

[9]Fonseca A F，Malta C P，Galvao D S.Mechanical properties of amorphous nanosprings[J].Nanotechnology，2006，17（22）：5620-5626.

[10]Goriely A，Shipman P.Dynamics of helical strips[J].Phys Rev E，2000，61（4）：4508-4517.

[11]Zhou Z，Lai P Y，Joós B.Elasticity and stability of a helical filament[J].Phys Rev E，2005，71（5）：052801（1-4）.

[12]Love A E H.A Treatise on the Mathematical Theory of Elasticity[M].New York：Dover，1944.

[13]Fate W A.High-temperature elastic moduli of polycrystalline silicon nitride[J].J Appl Phys，1975，46（6）：2375-2377.

Stiffness coefficients of normal and binormal helical springs

DAI Lu，ZANG Taocheng，GE Lijuan
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

With the aid of Cosserat curve theory，we investigated the stiffness coefficients of normal and binormal helical springs.The results show that the stiffness coefficients are not immune to the elongation in the entire stretching process.The binormal helical springs are quantitatively confirmed to excel over the normal ones in linear elasticity.Therefore，the binormal helical springs are more beneficial to the applications in engineering.

normal and binormal helical springs；Cosserat curve theory；stiffness coefficients

O469

A

1672－0687（2015）02－0037－04

責任編輯：李文杰

2014－10－04

國家自然科學基金資助項目（11347136）；江蘇省自然科學基金資助項目（BK20130265）

戴璐（1981-），女，江蘇蘇州人，講師，博士，研究方向：納米材料。