“等待時間”強余震預測方法的改進與應用——以尼泊爾地震為例
劉珠妹 李盛樂
1 中國地震局地震研究所(地震大地測量重點實驗室),武漢市洪山側路40號,430071
2015-04-25發生的尼泊爾Mw7.8(M8.1)地震是尼泊爾81a來遭遇的最強烈地震。此次地震強余震不斷,共發生Mw5 以上余震17 次,且地震破裂由西向東遷移,對我國西藏等地區造成一定的影響。
大地震發生后,對后續強余震發生時間的研究是震后趨勢判定的工作重點之一。谷繼成等[1]對我國1931~1977年28個地震序列進行研究,提出地震序列中相鄰余震之間“等待時間”規律,并以此判斷地震類型,以及進行大震后強余震發生時間的短臨預測。但在實際工作中,該方法更多地被用于地震序列類型的判定[2-4],而較少應用于強余震發生時間的預測[5-8]。本文首先從理論上對“等待時間”強余震預測法的殘差結構改變問題進行分析,在此基礎上給出了基于加權最小二乘擬合的模型改進方法,并將其應用于尼泊爾地震的強余震預測。
1 問題提出與模型改進
1.1 “等待時間”強余震預測模型
“等待時間”即一個地震序列中相鄰兩組強余震之間的時間間隔。谷繼成[1]發現,主余型地震序列中第i與第i-1個強余震的等待時間Δti與第i個強余震的發震時刻ti滿足以下關系:
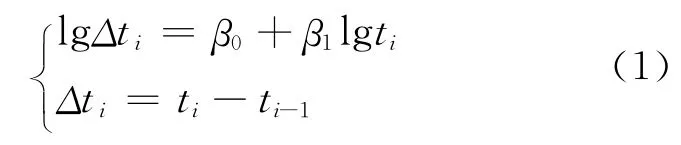
根據已知的地震余震序列,采用最小二乘法即可求得式(1)的線性擬合參數β0、β1,進而通過最近一次強余震的發震時間ti預測后續余震的發震時間。
1.2 基于加權最小二乘的強余震預測模型
“等待時間法”對觀測數據采用了對數變換,使其滿足線性模型假設。但同時,對數變換也改變了模型殘差的方差性質。在最小二乘求解線性方程時,改變了最小二乘法的準則函數[9]。
設Δt為相鄰強余震的等待時間,t為強余震的發震時間,則“等待時間-發震時間”模型的普通最小二乘準則函數為:
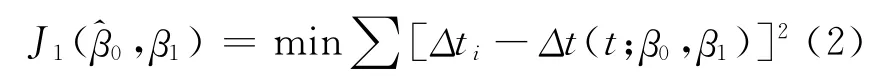
而對數變換后的最小二乘準則為:
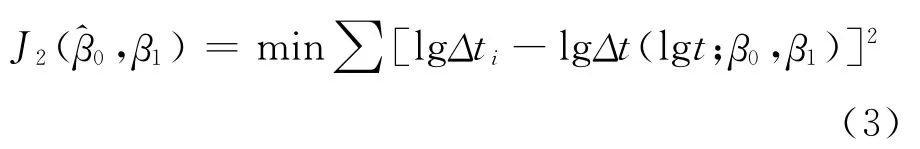
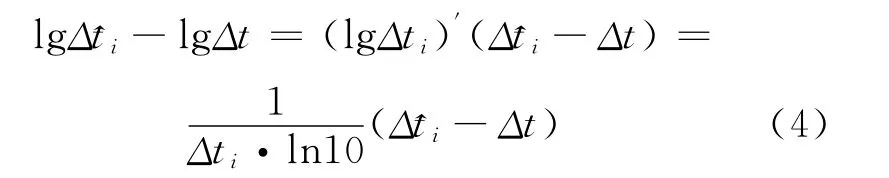
從而
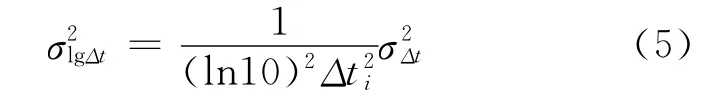
忽略常數項,對數變化后的最小二乘準則函數變為:
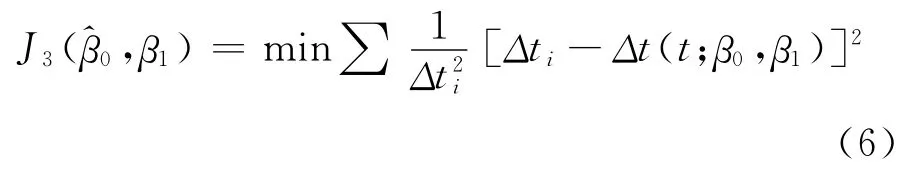
將原始“等待時間-發震時間”數據作對數變換相當于對原始數據進行加權,且權值為。加權的結果導致等待時間Δt值較小時,權值較大;隨著能量的衰減,相鄰兩次強余震等待時間增大時,權值較小。因此利用普通最小二乘法求解擬合參數時,最近的余震樣本距主震發震時間較遠,權值較低,對下一次強震時間預測控制力不足,從而影響預測的精度。
為抵消上述加權結果,在對數變換后線性擬合時,同樣可對數據加權:
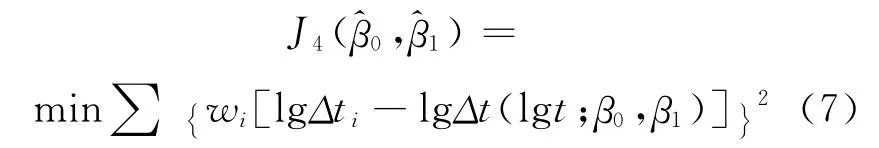
令權值wi=Δti,即可在一定程度上彌補雙對數變化對余震預測誤差的影響,從而提高預測的精度。利用加權改進的“等待時間法”進行強余震預測的流程見圖1。
2 尼泊爾地震強余震預測
2.1 余震目錄準備
谷繼承[11]建議,對于7 級以上強震,一般篩選低于主震2.5~3級的余震作為已知樣本進行后續預測,確定合適的序列震級下限。本文分別針對尼泊爾地震Mb4.5、Mb5以上余震目錄進行“等待時間”分析。數據采用美國ANSS 地震目錄,時 間 截 至05-12 07:05(UTC 時)發 生 的Mw7.3強余震。
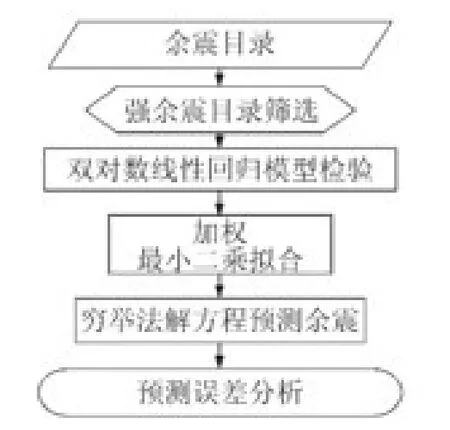
圖1 “等待時間法”強余震模型預測流程Fig.1 Flow of waiting time prediction for strong aftershocks
圖2(a)中余震下限為Mb4.5時,序列在“發震時間-等待時間”雙對數坐標軸中的線性擬合決定系數R2為0.68,樣本均方誤差MSE為0.26,余震序列分布較分散,不適宜進行后續余震時間預測;而圖2(b)中,5級以上余震序列線性擬合決定系數R2為0.95,MSE為0.06,線性關系更為顯著,序列分布更集中。因此,選擇Mb5以上尼泊爾余震目錄進行“等待時間”強余震預測實驗。
表1 給出了尼泊爾Mw7.8 地震序列中Mw5.0以上地震目錄,并計算每個余震樣本距離主震的發震時間ti、等待時間Δti和各自的對數值。其中序號13的余震與后續余震的間隔時間(0.28h)小于前一個強余震等待時間(7.88h)的1/20,文中將其視為同一次能量釋放,取較大震級的余震參與分析[11]。
修正目錄前后,樣本的線性關系發生明顯變化。圖3(a)中,未篩選目錄擬合系數R2為0.532,修正后R2提高到0.873,達到0.01的顯著水平(圖3(b))。
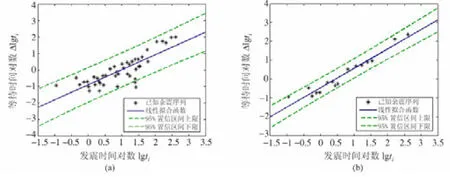
圖2 不同余震下限樣本的線性關系Fig.2 The linear relationship of samples with different minimum magnitudes
2.2 實驗分析
選取整個序列中通過線性回歸R檢驗及F檢驗,表現為顯著線性關系的N個樣本進行多組強余震預測實驗。首先對樣本分別進行普通最小二乘擬合和以Δti為權值的加權最小二乘擬合。將線性擬合參數β0、β1代入式(1),得到擬合線性方程。再窮舉Δt=i(i=1,2,3,…,n),tN+1=tN+ΔtN-1/20+i,作出窮舉線(圖4)。窮舉線與擬合線的交點即為預測的第N+1個強余震,交點x坐標值經乘冪變換后即為強余震的發震時間。
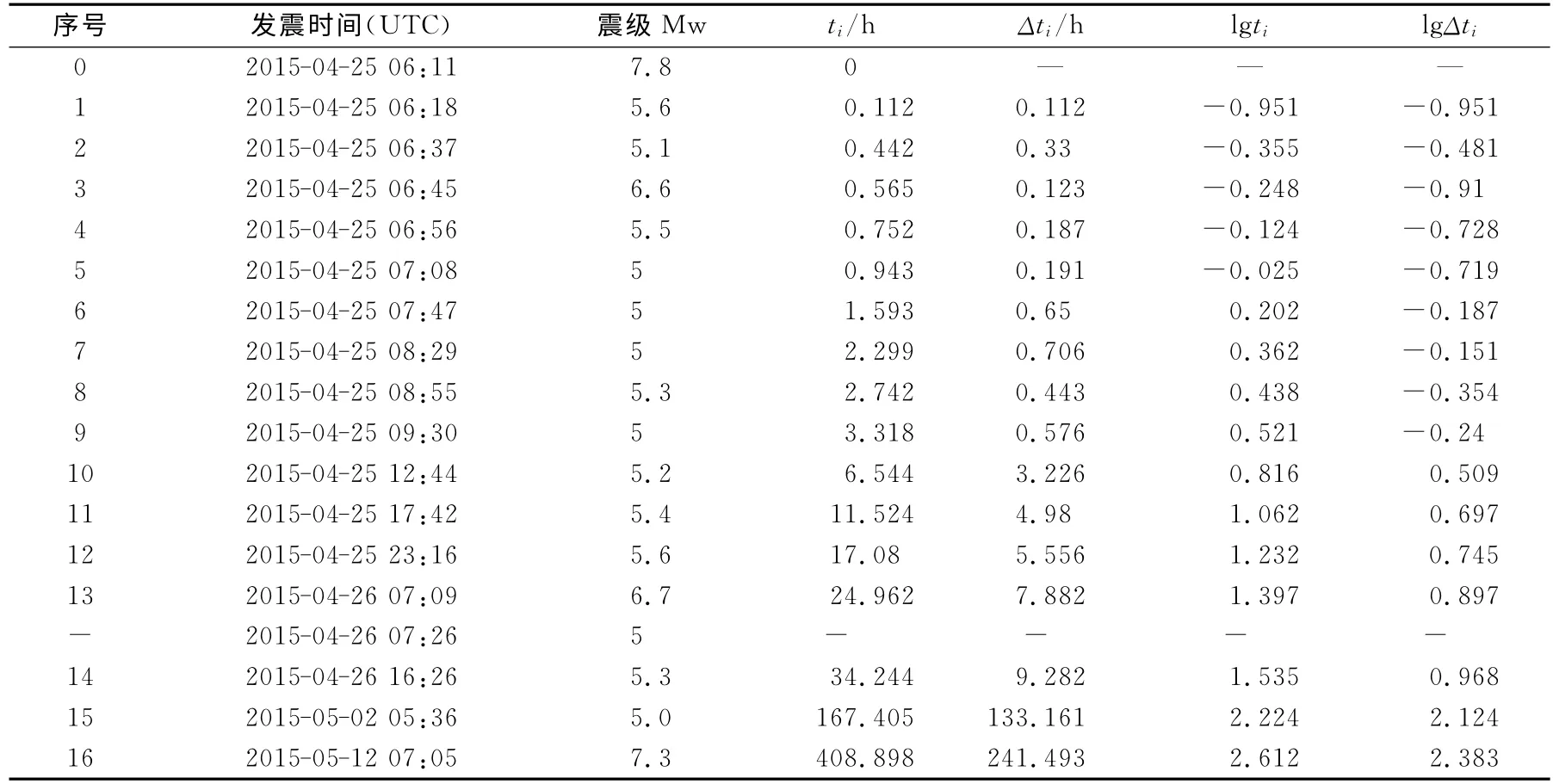
表1 尼泊爾Mw7.8地震5級以上余震序列統計表Tab.1 Mw7.8Nepal earthquake sequences with Mw≥5.0
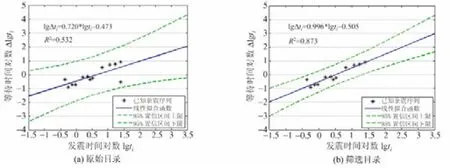
圖3 篩選目錄前后樣本的線性關系Fig.3 The linear relationship of samples before and after sequence sieving
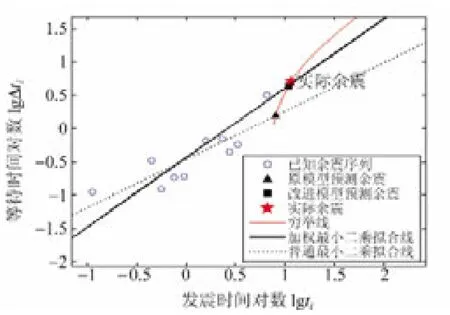
圖4 窮舉法求解余震發震時間(樣本數N=10)Fig.4 Solving equation by exhaustion methods(sample number=10)
表2中“最大樣本時間”指參與建模的最后余震距主震的發震時間。除N=11/13的兩組實驗外,其他5組經過加權改正的余震預測精度均有不同程度的提高。總體平均絕對殘差由原模型的0.173降為0.16,模型預測精度得到改善。預測的置信區間跨度也由原模型的0.590 縮小為0.125,說明預測結果的不確定性降低,預測實用性有了一定的提高。
3 分析與討論
為進一步驗證加權改正模型的適用性,本文另選取幾組典型的7級以上主余型地震的強余震樣本進行模型改正前后的強余震預測對比實驗。表3給出不同震例分別采用普通最小二乘和加權最小二乘得到的后續余震預測值、預測殘差以及真實發震時間與實際誤差。
由表3 及圖5 可見,經過改進的“等待時間法”應用于多個震例后,模型預測精度均有不同程度的提高。精度提高最大的烏恰震例,原模型預測誤差為0.323,模型改正后預測誤差減小為0.014。蘆山余震預測誤差,也由0.112 減小為0.071。6 個震例的平均絕對殘差由原模型的0.24降為0.045,平均降幅高達71%。
雖然經過模型改正后,余震預測的誤差有了不同程度的降低,但由對數模型轉化為真實時間后,實際預測誤差卻長達數10h,甚至上百h。由表3可見,于田、通海等震例改正模型的預測誤差均小于0.1,而轉化為實際時間后,后續余震的預測發震時刻和實際發震時刻相差長達4~5d。
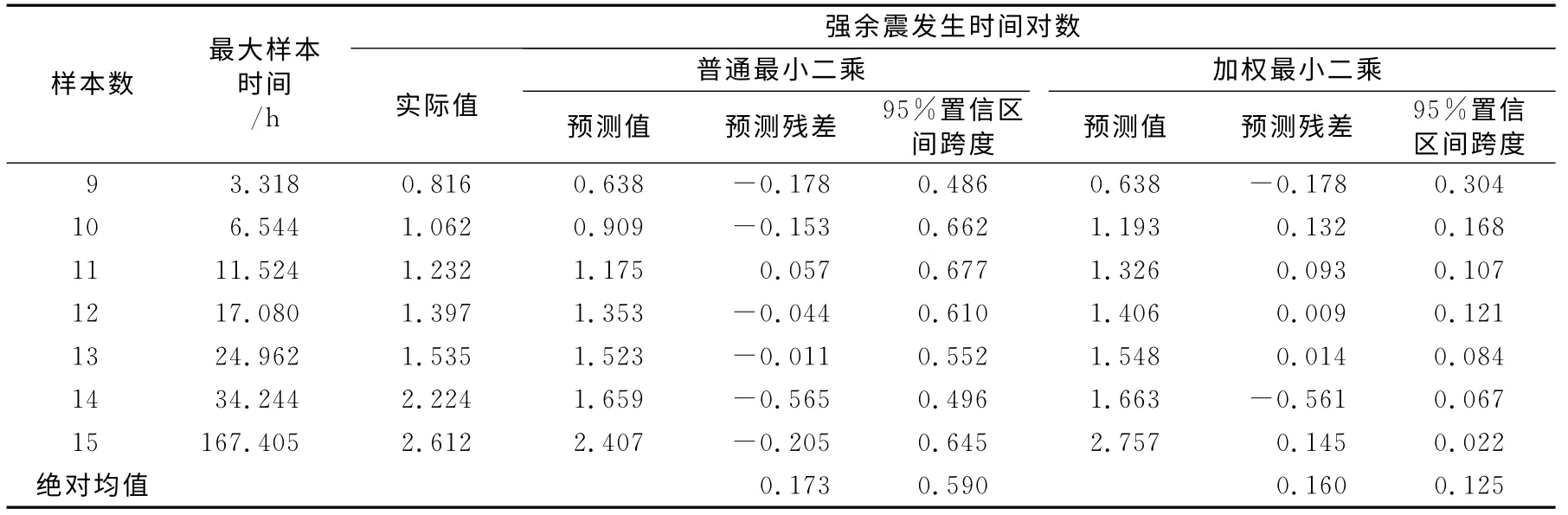
表2 原模型和加權改正的“等待時間”余震預測結果統計Tab.2 Statistical results of aftershock predictionwith two methods
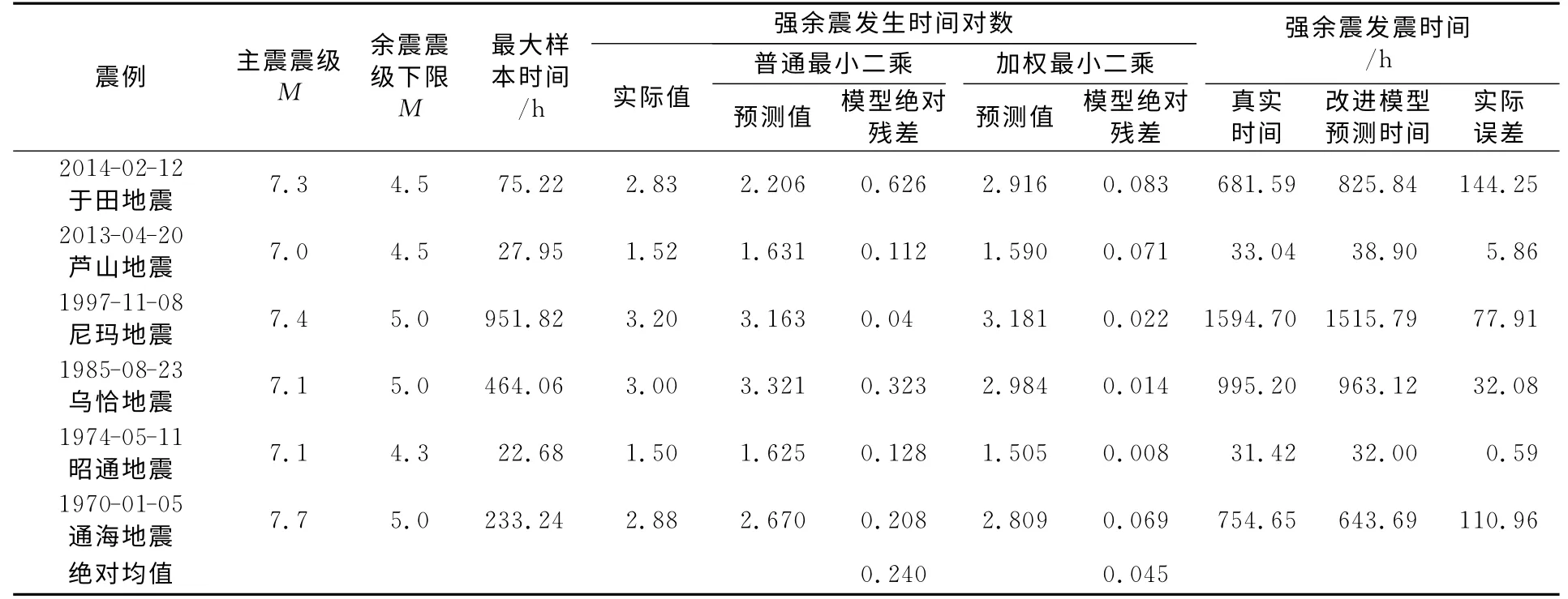
表3 典型震例的“等待時間”法強余震預測分析結果統計Tab.3 Statistical results of aftershock prediction among typical earthquake instances
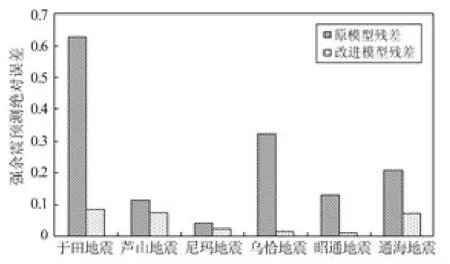
圖5 多震例的模型改正前后預測誤差比較Fig.5 Error comparation of predicting model before and after correction
圖6將樣本距主震時間分組為“1d以內”、“3 d以內”、“7d以內”、“15d 以內”以及“15d 以上”,分析模型誤差、實際誤差與樣本天數的關系。由圖中可知,改進后的預測方法雖然模型誤差控制在了較小的范圍內(<0.1),但隨著發震時間的推移,3d以后實際時間誤差可達數天,已不滿足應急所需。由于“等待時間法”樣本數要達到5個以上才具有穩定的擬合結果,對于短時間內發生較多強余震的主余型震例,利用本文方法進行強余震預測有效性較高;反之,對強余震發震較稀疏、時間跨度較大的震例而言,利用“等待時間法”進行余震預測的效率則不甚明顯。
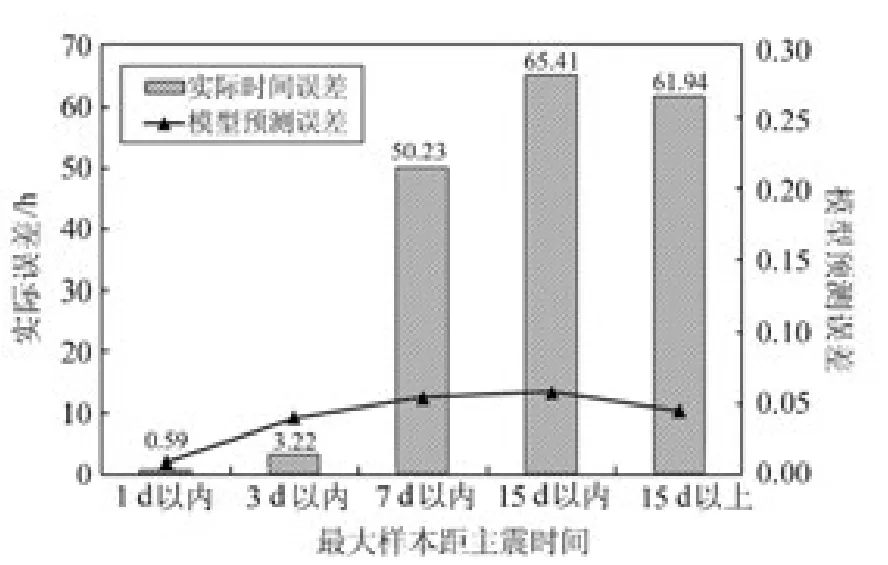
圖6 模型誤差和實際誤差與樣本時間的關系Fig.6 Relationship among model error、true error and sample time
[1]谷繼成,謝小碧,趙莉.強余震的時間分布特征及其理論解釋[J].地球物理學報,1979(1):32-46(Gu Jicheng,Xie Xiaobi,Zhao Li.On Temporal Distribution of Large Aftershocks of the Sequence of a Major Earthquake and Preliminary Theoretical Explanation[J].Chinese Journal of Geophysics,1979(1):32-46)
[2]蔣海昆,黎明曉,吳瓊,等.汶川8.0級地震序列及相關問題討論[J].地震地質,2008(3):746-758(Jiang Haikun,Li Mingxiao,Wu Qiong,et al.Features of the May 12 M8.0 Wenchuan Earthquake Sequence and Discussion on Relevant Problems[J].Seismology and Geology,2008(3):746-758)
[3]華愛軍,刁守中,王紅衛.強余震“等待時間”判別方案預報效能的研究[J].地殼形變與地震,1996(2):47-52(Hua Aijun,Diao Shouzhong,Wang Hongwei.Study on Prediction Ability of Method for Distinguishing the Waiting Time of Strong Aftershock[J].Crustal Deformation and Earthquake,1996,16(2):47-52)
[4]孟令媛,周龍泉,張小濤,等.2014年新疆于田Ms7.3地震序列和震源特征初步分析[J].中國地震,2014(2):159-167(Meng Lingyuan,Zhou Longquan,Zhang Xiaotao,et al.Study the Characteristics of the Yutian,Xinjiang Ms 7.3 Earthquake,February 12,2014[J].Earthquake Research in China,2014(2):159-167)
[5]曲延軍.新疆部分地震的余震序列特征及強余震預報[J].內陸地震,1990(1):87-96(Qu Yanjun.The Characteristics of Aftershock Sequence and the Prediction of Strong Aftershock in Some Parts of Xinjiang[J].Inland Earthquake,1990(1):87-96)
[6]秦乃崗.廣東及鄰區地震頻度衰減系數和余震等待時間[J].華南地震,1990,10(4):42-49(Qin Naigang.The Method of Earthquake Frequency Attenuation Coefficient and Aftershock Duration Time Applied in Guangdong[J].South China Seismological Journal,1990,10(4):42-49)
[7]趙小艷,韓立波,徐甫坤,等.2014年云南魯甸6.5級地震序列跟蹤分析研究[J].地震研究,2014(4):508-514(Zhao Xiaoyan,Han Libo,Xu Fukun,et al.Research on Tracking Analysis for Ludian Ms6.5 Earthquake Sequence in Yunnan in 2014[J].Journal of Seismological Research,2014(4):508-514)
[8]平建軍,劉榮環,賈炯,等.地震序列較強余震灰色及最小二乘擬合預測方法的應用研究[J].華北地震科學,2005(1):6-13(Ping Jianjun,Liu Ronghuan,Jia Jiong,et al.The Application Study of the Predict Method of the Gray and the Method of Least Square in the Earthquake Array Strong Aftershock[J].North China Earthquake Sciences,2005(1):6-13)
[9]耿鴻江.對數變換的問題及其改進[J].水文,1996(2):13-16(Geng Hongjiang.Problems in the Logarithmic Transformation and Improvements[J].Journal of China Hydrology,1996(2):13-16)
[10]楊安華,彭清娥,賀昌政,等.雙對數模型對模型模擬誤差的放縮問題探討[J].數學的實踐與認識,2006(8):135-139(Yang Anhua,Peng Qinge,He Changzheng,et al.The Discussing of the Problem of Enlarging or Reducing Simulation Error by Double Logarithmic Model[J].Mathematics in Practice and Theory,2006(8):135-139)
[11]谷繼成.地震類型的判別與強余震的預測[J].地震,1987(6):1-9(Gu Jicheng.A Method of Distinguishing Earthquake Type and of Predicting Large Aftershocks[J].Earthquake,1987(6):1-9)

