基于加權L1極小化模型選擇線性回歸模型中的自變量求解

李立亞,鄭桃云

（1.湖北第二師范學院 數學與統計學院，武漢 430205；2.湖北中醫藥大學護理學院，武漢 430065）

1 問題的提出

在上述介紹中，我們了解了自變量選擇的幾個準則，以及幾種自變量選擇方法的基本思想。從中可以知道經典的自變量選擇有局限性：自變量的所有可能子集構成了2m-1個回歸方程，當可供選擇的自變量不太多時，用全局擇優法可以求出一切可能的回歸方程，然后用幾個選元準則去挑選出最優的方程，但是，當自變量的個數較多時，要求出所有可能的回歸方程是非常困難的。還有就是，根據不同的方法和準則，選出的最優回歸模型也不一定相同，真正哪個回歸模型最優，同樣面臨選擇的困難。逐步回歸法也有明顯的不足之處：前進法不能反映引進新的自變量后的變化情況，因為某個自變量開始可能是顯著的，但當引入其他自變量后它就變得不顯著了，但是也沒有機會將其剔除，即一旦引入，就是“終身制”的；后退法同樣存在類似的問題，一旦某個自變量被剔除，他就再也沒有機會重新進入回歸方程，而且一開始把全部自變量引入回歸方程，這樣計算量很大；即使是吸收了前進法和后退法的優點，克服了它們的不足的最受歡迎的逐步回歸法，也有它的不完美的地方，即當自變量的個數達到幾百個，甚至更多上千萬個的時候，它也會慢慢失去其相對的優越性，不能成為我們理想的線性回歸模型的選元方法。

本文主要采用?1極小化模型在線性回歸模型中自變量選擇上的應用，即通過?1極小化理論和數據的稀疏性的應用，從所有可能的回歸系數矩陣β中選出含零元最多的一個，那么線性回歸中對應零元系數的自變量便可以舍去。這樣便大大的減少了自變量的個數，從而減輕了回歸的計算量并且能保持回歸模型的質量。

2 利用?1極小化模型選擇線性回歸模型的自變量

2.1 普通最小二乘法的參數估計

在一個實際問題的線性回歸建模中，有m個可供選擇的自變量 x1，x2，…，xm，因變量為y，并對該問題進行n次觀測，所得數據為(X1，X2，…Xm，y)。其線性回歸模型為

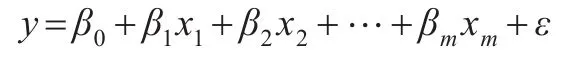
其中，β0，β1，β2…βm是 m+1個未知參數，β0稱為回歸常數，β1，β2…βm稱為回歸系數，回歸系數代表了每個自變量對回歸模型所做貢獻的大小，系數越大，貢獻也越大；系數為零，沒有貢獻，則該自變量可以舍棄。ε是隨機誤差，我們假定誤差項ε服從正態分布，即ε～N(0，σ2)

用矩陣表示該線性回歸的一般式，令：

性回歸模型為：

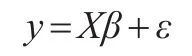
其中X是一個n×(m+1)階矩陣。對該線性回歸模型用普通的最小二乘法計算參數估計值，即求使觀測值與回歸值的離差最小下的參數：

當（X'X）-1存在時，即可得回歸參數的最小二乘估計為：

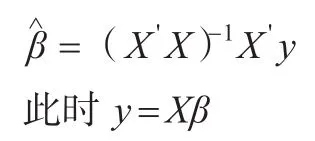
2.2 ?1-minmization model

最小二乘法是用所有的自變量來做線性回歸，并沒有起到回歸選元的作用。而經典的線性回歸選元方法，對自變量的個數較多時回歸效果并不好。如今人們發現可以通過?1極小化理論和數據的稀疏性來大大的減少自變量的個數且能保持回歸模型的質量：要使線性回歸模型y=β0+β1x1+…+βmxm+ε簡單而高效，我們可以減少不必要的自變量來減輕計算量，由于回歸系數代表了每個自變量對回歸模型所做貢獻的大小，系數越大，貢獻也越大；系數為零，沒有貢獻，則該自變量可以舍棄。那么只要使自變量對應的回歸系數估計值βi盡可能為零就可以達到此目的，即使參數估計值盡可能的稀疏。由?1極小化理論中信號的稀疏表示原理可知，即求

又因為?1最小范數在一定條件下和?0最小范數具有等價性，可得到相同的解。而且相較?0最小范數，?1最小范數更具有優勢，它便于計算。由于?0最小范數是要求向量元素不為零的最小個數，它是一個NP難題，要求這個問題是很難的。而?1最小范數是要求向量元素之和的最小值，它將非凸化問題轉化為凸化問題來求最優化求解，即將求?0范數的NP難題轉變為求?1范數的線性問題來找到信號的逼近，針對極小化?1范數模型來提出線性規劃方法，這個問題的求解方法有很多，更便于計算。所以可以替換（2）如下：

2.3 加權?1-minmization model

（4）當收斂或?達到指定的最大迭代次數?max時終止程序。否則，增加?并回到第2步驟。

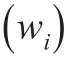
2.4 加權?1極小化模型選擇線性回歸模型的自變量

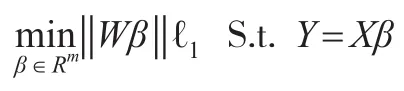
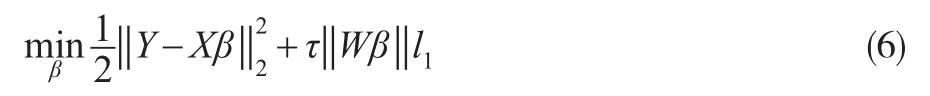
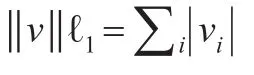
接下來將式子(6)轉變為一個二次規劃形式，它是通過將所求變量β分為兩部分完成的，通常稱這兩部分為積極和消極的部分，設：

2.5 GPSR(稀疏重建的梯度投影)法求解二次規劃問題

（4）當執行到給定的最大次數或有滿足的近似解

3 結果

3.1 仿真數據結果

用仿真方法來證實：加權?1極小化模型能有效地選擇線性回歸模型中的自變量。仿真數據從如下線性回歸模型產生：

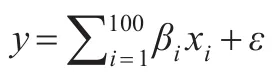
在上述回歸模型中，所含參數的個數為100個，第2，3，5，7，9個參數不為0，其它參數均為0；殘差項服從均值為0，標準差為0.1的正態分布。假設自變量均是0-1之間的均勻分布的隨機數。利用Matlab自帶函數生產隨機數的方法，產生50組樣本值及每組樣本值相應的殘差項，根據上述回歸模型，可計算相應因變量的值。因變量的值如圖1所表示。

由這50組樣本數據和相應的因變量的值，需要估計回歸分析模型中參數的值。明顯的，利用普通的線性回歸模型中的最小二乘法，因這些數據只能構造50個線性方程，無法準確的估計真實的參數。然而，利用加權?1極小化模型，可以幾乎完美的估計出真實的參數。如圖二所表示。原因在于加權?1極小化模型，它除了利用數據提供的信息之外，還能有效的利用待估參數先驗信息，即稀疏性。而普通的線性回歸模型中的最小二乘法只能利用數據提供的信息。

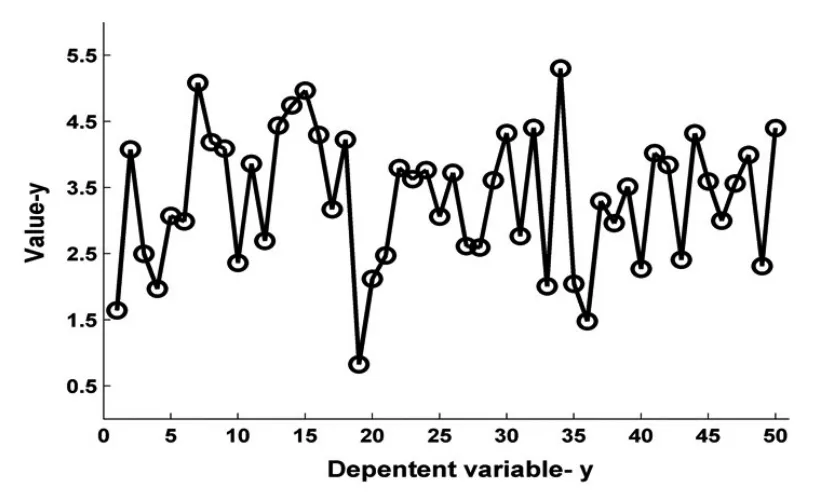
圖1 為仿真產生的50組樣本值所對應的因變量的值

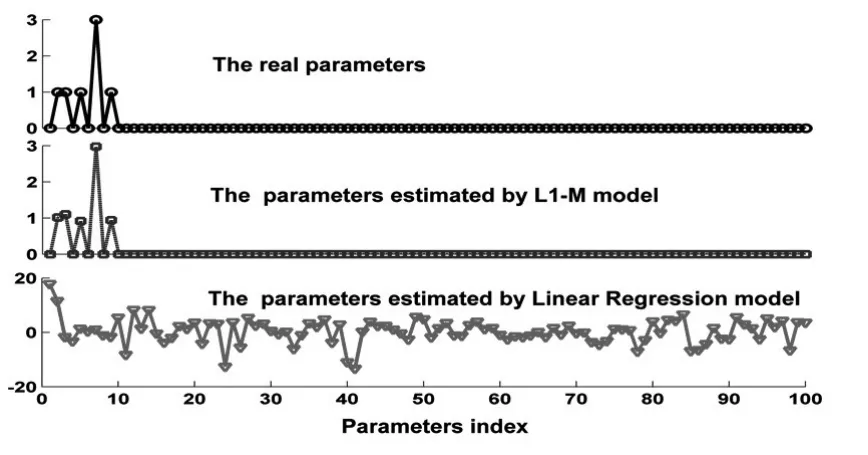
圖2 L1極小化模型對線性回歸系數的有效性

該仿真模型結論表明：利用加權?1極小化方法求得的回歸系數估計值的非零個數，遠遠小于最小二乘法求出的個數，且它極為接近原先設定的較為稀疏的實際系數值，幾乎可以完全模擬出實際的自變量系數。由于回歸系數為零的自變量對因變量沒有任何貢獻，可以剔除，所以，該方法可以大大的減少自變量的個數，起到線性回歸選元的作用。

3.2 實驗數據結果

本文選取2009年《中國統計年鑒》我國30個省、市、自治區（西藏地區失業率數據缺失，因此從樣本中剔除西藏）2008年的數據。

現實生活中，影響一個地區居民消費的因素有很多，例如，一個地區的人均生產總值、收入水平、消費價格指數、生活必需品的花費等。本例選取9個解釋變量研究城鎮居民家庭平均每人全年的消費性支出y，解釋變量為：x1居民的食品花費，x2居民的服裝花費，x3居民的居住花費，x4居民的醫療花費，x5居民的教育花費，x6地區的職工平均工資，x7地區的人均GDP，x8地區的消費價格指數，x9地區的失業率。本例題以居民的消費性支出（元）為因變量，以如上9個變量為自變量，其中，自變量x1，x2單位為元，x9單位為%。文中利用加權?1極小化模型來這些對自變量作變量選擇，并用Matlab編寫程序。

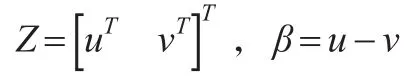
β=[1.2083-0.5232，0-0，0.5550-0.3883，0-0，0-0，0.7376-0.5023，0.5147-0.3591，0-0，0-0]=[0.6851，0，0.1667，0，0，0.2353，0.1556，0，0]

其中，第2、4、5、8、9個回歸系數元素為零，則其對應的自變量對因變量沒有任何影響，即可以剔除x2、x4、x5、x8、x9。所以，剩下的自變量 x1、x3、x6、x7為程序挑選的自變量，可建立最優的線性回歸模型。即居民的食品花費，居民的居住花費，地區的職工平均工資，地區的人均GDP是建立線性回歸方程的最優自變量，對所求因變量居民的消費性支出起到顯著的影響。

該結果與實際是非常相符合的。我們知道現今社會，大部分人們的消費支出都用在了衣食住行上，但并不是它們都很重要，因為人可以不趕潮流，不買新衣服，但卻不能不吃飯，不租房睡覺，所以，居民的食品花費（x1）和居民的居住花費（x3），對居民的消費性支出有很大的影響，而居民的服裝花費（x2）不及它們的影響程度。同時，只要人們好好對待自己的身體，養成良好的作息習慣，就可以避免大量的醫療花費；而且由于地方省市的經濟大不相同，有的地方人們生活水平高，可以享受良好的教育環境，而有的地方人們食不果腹，接受教育無從談起，所以，居民的醫療花費（x4）和居民的教育花費（x5），對居民的消費性支出并沒有很大的影響。有工資就有錢來消費，人均GDP高的地方人們的生活水平就高一些，人們大多有錢用來消費，所以，地區的職工平均工資（x6）和地區的人均GDP（x7），是顯著的影響因素。而（x8）地區的消費價格指數和（x9）地區的失業率對不同的地區不盡相同，并不能成為顯著的影響因素。綜述所述，挑選居民的食品花費，居民的居住花費，地區的職工平均工資，地區的人均GDP為建立線性回歸方程的最優自變量，是非常符合實際情況的。另外，我們比較了最小二乘法與加權?1極小化方法所得到的參數估計值，見下表。

表1 最小二乘與加權?1極小化模型得到的待估參數

可以看出利用加權極小化模型所得到的回歸系數估計值更為簡單，且更合理。表一中最小二乘法得到的回歸系數值都不為零，不能舍去任何自變量，并沒有起到線性回歸選元的作用，而且這些回歸系數并不是能很好的解釋因變量的變化。因為消費性支出是指用于家庭日常生活的全部支出，包括食品、衣著、居住、家庭設備用品及服務、醫療保建、交通和通信、娛樂教育文化服務、其他商品和服務八大類等，所以將居民的醫療花費（x4）和居民的教育花費（x5）的回歸系數定義為負數是不合理的。反觀加權極小化模型，它求得的回歸系數值更為稀疏，可以舍棄許多不必要的自變量，減少計算量，極為有效的挑選出顯著的影響因素，得到最優線性回歸方程。

[1]何曉群，劉文卿.應用回歸分析（第二版）.北京：中國人民大學出版社，2011.

[2]石光明.劉丹華.高大化.劉哲.林杰.王良君壓縮感知理論及其研究進展-ACTA Electronica Sinica 2009，37(5).

[3]Donoho D.Tsaig Y Extensions of Compressed Sensing[J].Signal Processing,2006，(3).

[4]Candes E J,Wakin M B,Boyd S P.Enhancing Sparsity by Reweighted?1Minimization[J].Journal of Fowrier Ana Lysis and Applications,2008,14(5).