基于線性混合模型的風險相依信度模型構建
李政宵,謝遠濤,蔣 濤
(1.中國人民大學統計學院,北京100872;2.對外經濟貿易大學a.保險學院b.金融學院,北京100029)
0 引言
在許多團體保險業務中,保單之間通常具有很強的相關性,使得傳統信度模型在定價過程中會出現一定的偏差。同時傳統的信度模型運用非參數估計的方法估計結構參數,使得在實際運用中誤差偏大。Frees(1999,2001)[1]認為基于縱向數據在線性混合模型下的隨機效應的最佳線性無偏預測(BLUP)[2]可以分解出信度因子,并將B-S信度,Jewell分層信度[3]和Hachemeister回歸信度作為混合模型的特例進行實證研究[4]。至此,線性混合模型逐漸代替信度模型成為廣泛使用的經驗費率厘定的工具。
本文從傳統統計的思路出發,擴展了Frees(1999,2001)的研究,認為隨機效應和殘差間的相關性不再局限于特殊的形式。通過引入四種不同的協方差矩陣,解釋縱向數據之中存在的四種不同的相關結構。本文發現,數據間的相關結構會影響信度保費預測值的表達式。雖然信度預測值不再以線性形式表出,但是仍然能從理論上分解出信度因子,并滿足信度因子的特性。最后本文運用Hachemeister(1975)的縱向數據,探究不同形式協方差矩陣下隨機效應和固定效應的估計值以及信度因子的“收縮效應”,分析了數據間相關性對信度表達式的影響,為信度模型擴展提供相應的理論依據。
1 線性混合模型
在非壽險精算中經驗費率厘定中,信度定價基本的思想是在經驗數據和整體保單組合信息的基礎上,預測個體的未來賠款額度。而線性混合模型可以用來對縱向數據建模并預測,固定效應包含了個體歷史經驗信息,隨機效應則用來描述同一風險類別下保單的異質性(隱藏的風險特征)。因此,本文可以將線性混合模型和信度理論結合起來一起研究。
線性混合模型表示如下:
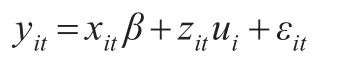
其中yit表示第i個個體在時間t的數據,i=1,2,...,n ,t=1,2,...,T(假設每個體都包含T 個觀察值),xit為固定效應解釋變量,zit為隨機效應解釋變量
矩陣形式表示如下:
y=Xβ+Zu+ε
其中殘差和隨機效應滿足下述假定:
(1)E(εi)=0 Var(εi)=Ri
(2)ui為隨機變量,期望與方差表示為 E(ui)=0,Var(ui)=Di
(3)殘差與隨機效應獨立,即 Cov(εi,ui)=0
響應變量y的協方差矩陣由兩部分構成:殘差的協方差矩陣R以及隨機效應的協方差矩陣ZDZ'。固定效應值影響y的期望值,隨機效應只影響y的方差,衡量了數據間的離散程度。在信度理論中,固定效應可以解釋為索賠平均值,信度預測值在均值的基礎上通過隨機效應進行調整。為了研究方便,本文假設 y的方差為:Var(y)=V=ZDZ'+R。因此響應變量 y服從期望為Xβ,方差為V 的多元分布,即 y~(Xβ,V)。
2 風險相依的信度模型
2.1 信度模型預期保費
保險數據的形式通常以縱向數據為主。下面根據線性混合模型的基本假定,建立縱向數據模型。數據結構為平衡數據結構(Balanced data),即每個單位個體有相同的觀察值,將個體記為 i(i=1,2,...,n),觀察值個數記為 j(T=1,2,...,T)。
第i個單位觀察值矩陣記為:

2.2 風險相依的信度模型
2.2.1 風險個體i之間獨立不相關
此時,隨機效應相關系數滿足ρu=0。y的方差矩陣簡化為
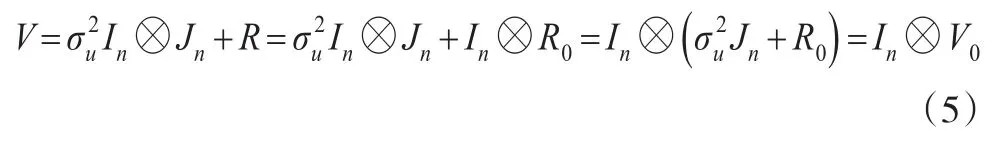

2.2.2 個體間獨立不相關,并且單位個體在不同時間上的觀察值也不相關。
此時滿足隨機效應之間的相關系數ρu=0,殘差的協方差矩陣滿足:

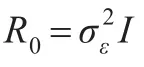
2.2.3 個體之間獨立不相關,即ρu=0。但是特定的風險個體在不同時間上的觀察值存在相關性。
殘差的協方差矩陣表示為

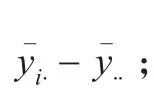
綜上所述,本文考慮了以上四種數據間的相關性情況,認為如果個體間和個體歷史觀察值之間都分別不相關,用線性混合模型得到的預測值可以分解為標準的Bühlmann信度公式,見表1。歷史觀察值之間的相關性會導致隨機效應的方差減小;相關性越高,個體之間的風險同質性越強,賦予其他個體間信息的權重越高;反之,相關性越低,個體之間風險異質性越強,賦予個體歷史經驗數據的信息的權重越高。另外,不同個體之間的相關性也會影響信度預測值的表達值。雖然信度預測值不能分離出信度因子的表達式,但預測值仍然可以看作個體歷史數據信息和組合信息根據權重進行調整,該權重從廣義上仍然可以解釋為信度因子。
2.3 特例B-S信度公式
本文探討了數據在組間和組內都不相關的假設下,估計結果可以由Bühlmann信度公式完全表示出。下面,沿著協方差矩陣形式(2):個體間獨立不相關,不同觀察值間殘差也不相關,將索賠頻率作為殘差協方差的權重引入線性混合模型模型中,殘差協方差矩陣形式調整為:
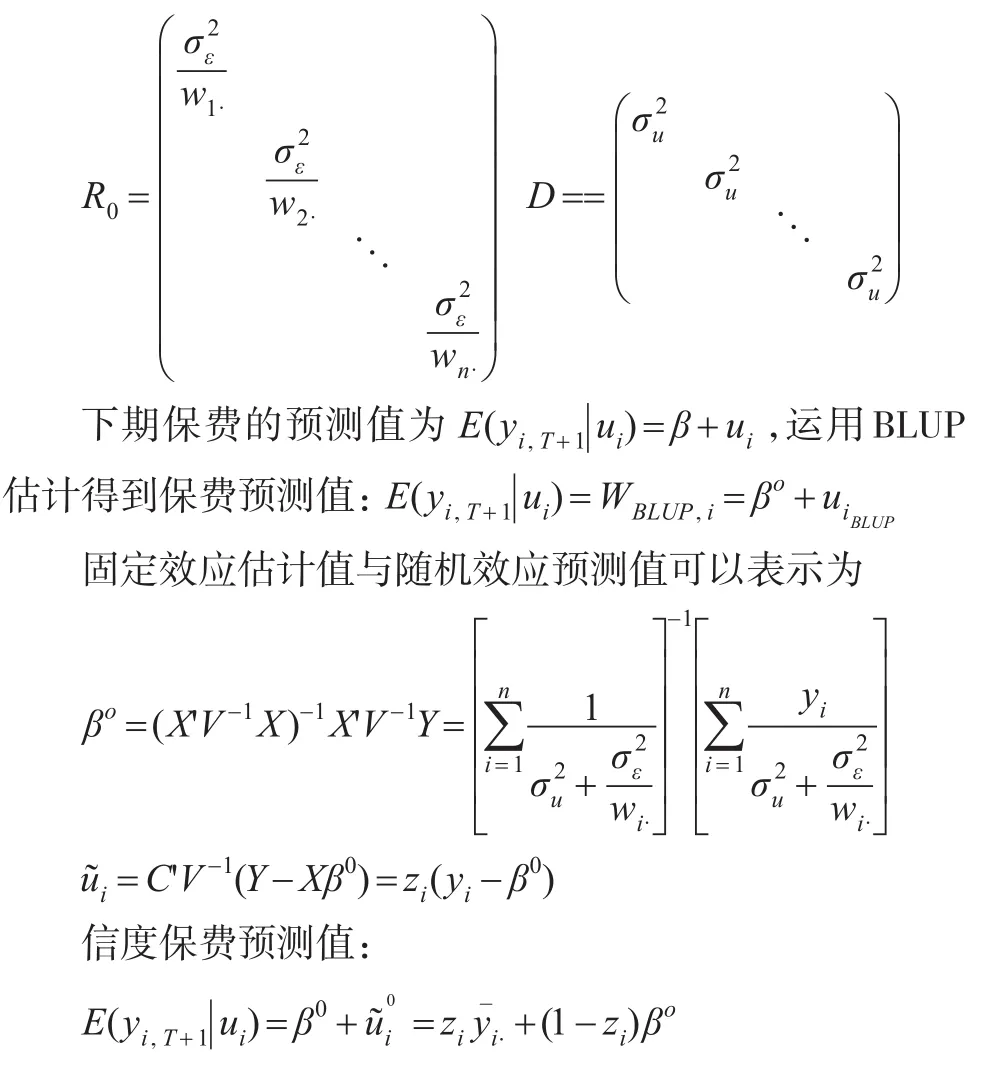

B-S信度公式不同于傳統Bühlmann信度公式在于:引入索賠頻率作為殘差協方差矩陣的權重后,信度因子不再是單一的值,而是隨著個體i的不同而不同,即滿足不同個體i都存在一個信度因子zi,對該個體的經驗數據和分類費率進行調整。
2.4 實證分析
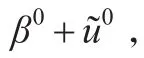
數據集包含美國6個州、12個月的汽車索賠強度和索賠次數的縱向數據。在線性混合模型的框架下,將每個州視為一個單位個體i,每個個體的觀察值T=12。本文選擇特例的B-S信度公式作為模型,引入索賠頻率對殘差協方差矩陣調整。
運用SAS統計軟件進行參數和方差估計,利用SAS中協方差矩陣(UN)的設定,在受限極大似然估計(REML)的估計方法下,得到固定效應的估計值(BLUE)和隨機效應的預測值(BLUP)(見表2)。
Frees(2001)指出通常情況下,信度因子具有“收縮效應”:個體經驗信息在信度預測值計算中起決定性作用,整體信息只是通過很小的權重進行調整,使得整體信息的定價作用收縮。根據實證結果,本文將得到的實際信度預測值與個體經驗信息(完全信度預測值)相比較,信度因子基本達到90%以上,即認為實際信度值與完全信度值存在較小差異。信度因子的“收縮效應”(shrinkage effect)見圖1。

表1 風險相依的信度模型
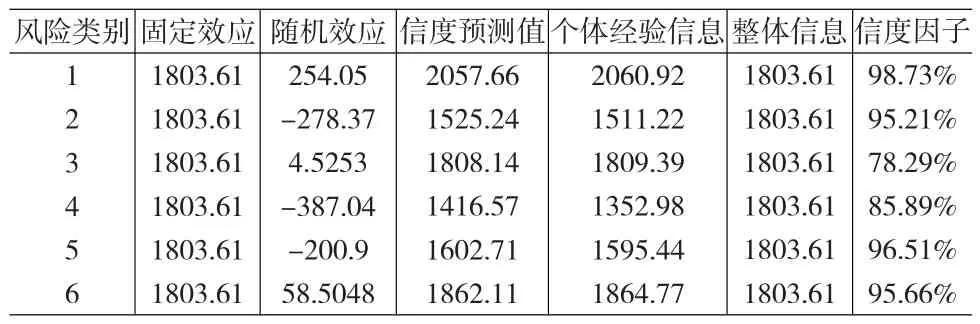
表2 估計值和信度因子
3 結論
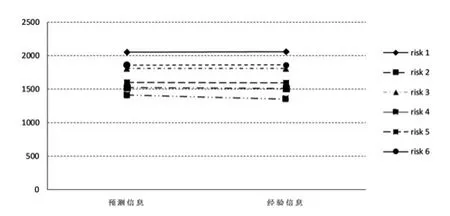
圖1 信度因子收縮效應
Frees(1997)通過線性混合模型模型推導出了4種著名的信度公式:Bühlmann信度,B-S信度,Hachemeister回歸信度和Jewell分層信度。但是其研究結果都是基于個體組間和組內相互獨立且不相關的假設。本文的創新點在于引入了4種協方差矩陣的形式建立組間和組內觀察值的相關性,探討了信度因子的不同表達形式,驗證了B-S信度下的線性混合模型模型分解出的信度因子的收縮特性。本文發現個體間的相關性會影響信度因子的表達式形式,即如果相互獨立,信度因子可以分離出與Bühlmann信度相似的表達式;反之,相關系數會對信度因子表達式進行調整,但仍然滿足信度因子的根本性質。另外一方面,殘差在個體觀察值之間的相關性會增加個體風險同質性的假設,使得信度因子減小,而從將更多的權重賦予其他個體的信息。
以上研究都是基于線性混合模型,由于考慮數據之間的非線性關系以及存在的右尾情況,將線性混合模型擴展到廣義線性混合模型(GLMMs)并嘗試分解出信度因子中是今后的研究方向。沿著隨機效應和殘差協方差矩陣的思路,通常認為引入copula回歸的結果比普通回歸的結果誤差更小,今后可以考慮用copula來研究個體間的相關性和個體觀察值之間的相關性,并構建相應的信度模型。
[1]Edward W.Frees,Virginia,Yu Luo.A Longitudinal Data Analysis Interpretation of Credibility Models[J].Insurance:Mathematics and Economics,1999,24(3).
[2]G.K.Robinson.That BLUP is a Good Thing:The Estimation of Random of effects,with Discussion[J].Statistical Science,1991,6(1).
[3]Jewell,W.S..The use of collateral data in credibility theory:a hierarchical model[J].Giornale dell'Instituto Italiano degli Attuari,1975,(38).
[4]Edward W.Frees,Virginia,Yu Luo,Case studies using panel data models[J].North American Actuarial Journal,2001,5(4).

