基于GARCH族模型的收益波動率預測績效評估方法

劉 青，戴經躍,楊 超

（1.遼寧師范大學 數學學院，遼寧 大連116029；2遼寧稅務高等專科學校 計統系，遼寧 大連 116023）

0 引言

波動率是金融經濟研究中的一個非常重要的變量，在金融市場中，無論是金融產品的投資組合、風險管理還是資產定價，波動率都扮演著非常關鍵的角色。如何對金融資產的收益波動率進行精確的描繪與預測是金融學領域關注的焦點之一。分析收益波動率的特性及走向，對投資者度量和規避市場風險均有重要的研究價值和實際意義。本文采用半參數方法估計GARCH族模型，并進行樣本外的一步外推（One-Step-Ahead）預測。EF方法在估計的過程中引入了收益率的偏斜和峰度信息，其估計結果比QMLE更高效。此外，與參數化的條件分布相比，EF方法不受限于具體的分布模式，這樣盡可能地降低了“模型風險”。EF方法與廣義矩估計（GMM）較為相似。不同之處在于，EF方法所使用的估計函數相當于GMM中的正交化處理功能，并依照一定的規則優化后的“矩條件”，其效率也高于GMM。本研究將分別采用這兩種方法進行估計和預測。此外，為了減少績效評估的“數據窺察”問題，給出統計意義下的結果，本文將采用最小二乘（OLS）方法進行模型績效對比。最后，檢驗結果發現，EGARCH模型能提供較為優越的預測效果。

1 GARCH族結構與參數估計

1.1 GARCH族結構描述

假定資產的收益率時間序列rt服從隨機分布rt|Ψt-1~D(μt，ht)，其中 Ψt-1為 t時刻的已知序列集。為了規避時間序列在1階矩上的自相關信息誤入2階矩，引入以下模型，

這里，截矩項μ0和滯后階數τ分別根據回歸的顯著性、殘差的Q統計量以及AIC信息準則決定；εt表示擾動項，基準擾動項zt條件在以往的信息上服從0均值單位方差的獨立同分布；ht=h(εt-1，ht-1，εt-2，ht-2，…)表示方差方程。每類GARCH族結構均根據一定的經驗發現并對h(·)作的不同變換。例如較常見的GARCH(1，1)模型，具有形式精簡、可理解的特點，基本形式如下式所示：

實際的波動曲線通常表現出較好的連續性，相關研究者提出了積分GARCH（IGARCH）：

此外，為了描述波動過程的非對稱性波動，采用較廣泛的指數型GARCH（EGARCH）：

從以上的模型構建中不難看出，一些模型之間存在相互重疊關系，例如GJRGARCH、AGARCH等都嵌套了GARCH基本模型。盡管模型之間存在較多的嵌套關系，但將這些被嵌套的模型納入“模型全集”有利于發現更加精簡的形式。這是由于若嵌套模型對被嵌套模型進行推廣，從波動率預測的視角來說并不必要，這樣，被嵌套的結構的參數估計將更為高效，繼而表現出更加有效的預測性能。

1.2 基于EF的參數估計策略

在傳統的GARCH族模型中，通常采用高斯分布下的極大似然法進行參數估計。由于金融資產的收益率曲線常顯示出偏斜和超額峰度特性。此時，QMLE盡管理論上仍能保持漸近一致性，但估計的效率較差。實際應用中，通常會綜合考慮預測的無偏性和效率性對模型的預測績效進行評估，如常用的“均方誤差”（MSE）指標。因此，QMLE方法在估計不同的模型時出現的效率代價，可能會改變MSE等指標對模型預測績效的評估結果。這就有必要采用比QMLE更為有效的參數估計方法。

由于在假定概率密度函數已知時，完全的參數化方法存在潛在的模型風險，因此，本研究將引入一種半參數方法——估計函數法EF，并將其應用到上述各族GARCH模型。此時，估計函數與GMM法中的矩條件較為類似，即找到一個連續可微的函數式 f(·)滿足下式

這里 Θ=(θ1，θ2)，θ1與 θ2分別是均值方程與方差方程中的參數序列；另外，Θ對應于隨機過程{rt|t=1，2，…，T}相應的概率空間。為了方便描述，不考慮條件信息集Ψt-1，并用Et(·)代表條件期望的計算函數。滿足式（5）的函數 f(·)稱之為正則函數。但與GMM方法中的矩條件具有差異性的是 f(·)滿足另一條件，即對?Θ=(θ1，θ2)，如下所示的Q 值均達到最小值，

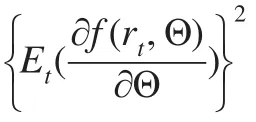
GARCH族模型中的正則函數可表示為如下：

2 一步外推預測與績效評估方法

2.1 滑動窗口的一步外推預測

為了避免過擬合問題，將{rt|t=1，2，…，T}劃分為T=S+F兩部分構成。這樣，將總體樣本更新為{rt|t=-S+1，-S+2，…，0，1，2，…，F}，待預測的時間序列為{ht|t=1，2，…，F}。采用滑動窗口的1步外推預測策略如下：（1）構建樣本估計模型{rt|t=-S+1，-S+2，…，0}，并預測 h1；（2）利用樣本{rt|t=-S+2，-S+3，…，1}預測 h2；根據以上步驟，在第k步，預測hk時所采用的樣本為{rt|t=-S+1+k，-S+2+k，…，k-1}，k=1，2，…，F 。 采用滑動窗口的一步預測法可允許訓練信息在模型中得以利用，還能提高模型在結構變化時的參數適應性。

這四種代價函數均為衡量模型預測的無偏性和效率性的有效指標，但不同的代價函數對異常點（Outlier）的敏感程度卻有所不同。因此，本研究將分別使用這四種代價函數對GARCH族結構的波動性預測績效進行測量。

2.2 預測的績效評估

2.2.1 已實現波動率

本文的研究將以“日”作為收益率的采樣周期。由于單日內的實際波動通常難以發現，因此我們以“已實現”波動作為替代變量，表示如下：

上式中，T表示一天內的樣本數量。不同于以往對代價函數的排序策略，本文將使用最小二乘（OLS）機制對6種GARCH族模型，分別利用QMLE和EF為參數策略時，四種預測的代價函數的差異進行對比和統計檢驗。

2.2.2 績效評估的最小二乘（OLS）檢驗

其中，截距c為模型m*與m分別采用d*和d作為參數估計策略時，代價函數的差異值。所以，截距c表示模型m*和m分別以d*和d為參數估計策略的相對代價；其中，m*，m=0，1，2，…，9 ，且 m*≠m ；d*，d=0，1。由于擾動項ξt存在潛在異方差和自相關現象，為了計算c的具有無偏性的標準誤差，擬合時采用NW方法進行微調。因此，如果c^顯著小于0，則表明標準模型m*以d*為參數時的預測性能顯著優于備選模型m以d為參數時的預測性能，反之則反。

3 實證研究

3.1 樣本描述

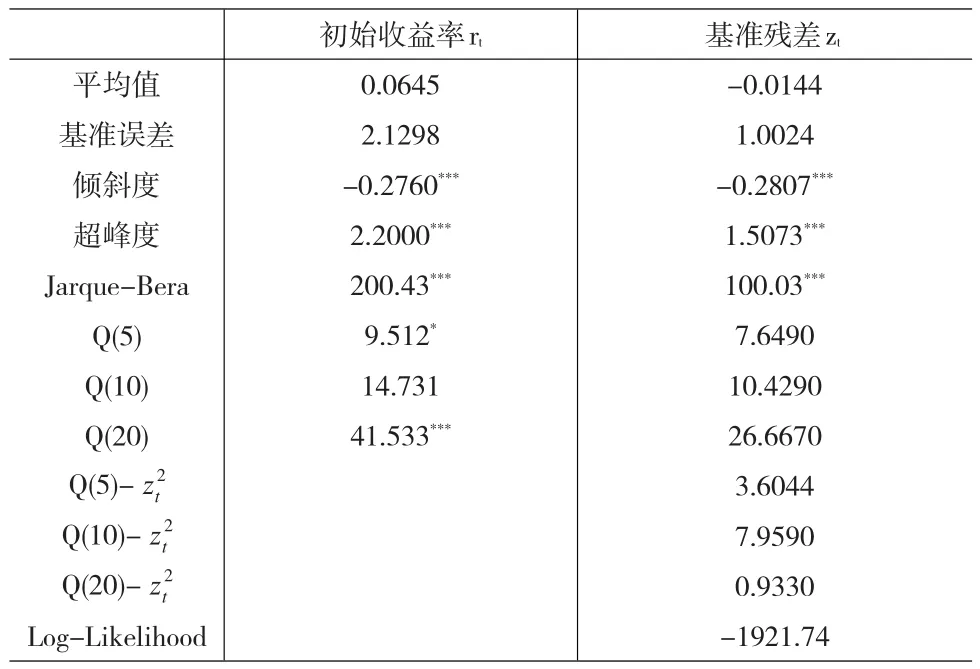
表1 上證綜指的初始收益率以及經AR(p)-GARCH擬合后的基準殘差的統計結果

表1中的統計量表明，由AR()p-GARCH擬合后，基準殘差的1階和2階矩上的自相關已基本抵消，意味著擬合后的基準殘差可等價于白噪聲過程。盡管如此，兩市的指數收益均有顯著的負傾斜度和超額峰度值，并且采用Jarque-Bera假設檢驗時，高斯模型被顯著拒絕了。這樣，描述性統計結果已初步表明高斯分布并不適合代表樣本數據的分布。

3.2 分析結果

研究中每種GARCH模型均采取滑動窗口的一步預測。將934天的最后100天作為外部觀察值。為了與現有的研究方法進行對比，我們也將高斯分布作為GARCH族模型的條件分布并作一步預測。表2顯示了4種代價函數下，6種GARCH結構的預測績效。圖1以柱狀圖的方式，直觀地顯示了4種代價函數下，各種GARCH結構的預測性能。

表2 高斯分布假設下GARCH族模型的波動率預測績效結果

圖1 基于QMLE方法的GARCH族模型的波動率預測績效

結合表2和圖1可觀察到，在高斯分布的假設下，采取QMLE估計策略來預測時，IGARCH是GARCH族模型中預測績效更好的一種異方差模式。然而，如圖2所示，基于EF方法的波動率預測結果與圖1所示結果具有一些差異。

圖2 基于EF方法的GARCH族模型的波動率預測績效

根據圖2中的結果，我們發現，采用MSE和MAE為評估指標時，IGARCH和AGARCH是較好的兩種異方差模式，而MAPE和HMSE的結果顯示，EGARCH模型的預測誤差相對較低。此外，與圖1對比，基于EF的波動率預測結果顯示各類GARCH結構的預測結果差異較大。這說明，QMLE方法在估計模型時存在的效率代價，使得各類模型的績效差異不會太大，即使最簡練的模型仍可呈現出最優的性能；而較為復雜的結構可能需要更加有效的估計策略，才可解釋其結構對數據特性的描述力。最終，圖2中的4種代價函數均表明，IGARCH結構是表現出較差的績效。為此，我們進一步考察采用OLS方法來對比各類GARCH結構基于QMLE和EF策略的預測性能，相關結果如表3所示。

表3 各類GARCH結構分別基于EF（基準模型）和QMLE方法的預測績效比較結果

表3中，方括號中數值代表基于EF方法的預測績效比QMLE方法提高的百分比，我們可觀察到，與QMLE方法相比，IGARCH結構在基于EF方法時的預測績效并未表現出較好的優越性。前兩種結構甚至顯著拒絕了EF方法的效果。除此之外的其它7種結構均顯示，EF方法與QMLE方法相比，可改善模型的預測性能。特別地，應用EF方法可以顯著改進EGARCH模型的預測性能。但由于EF方法引入了傾斜度和峰度等高階矩信息，因此，在模型確定可精確描繪收益率波動時，EF策略將有可能提高模型的預測性能。相反，如果模型設置錯誤，采用更為高效的EF策略也會進一步降低模型的預測性能。所以，根據表3的結果，相對于IGARCH結構，選取其它5種設定將更為合適。

圖3 QMLE和EF方法下預測績效好的GARCH族模型比較

為了進一步對不同的估計方法進行對比，我們將在IGARCH模型中使用QMLE策略的預測性能，以及在EGARCH結構中采取EF方法的預測績效加入同一個對比空間中。從圖3可以看出，采用EF方法預測中，性能較高的三種異方差結構均優于兩種QMLE方法預測性能高的模型。

綜上所述，與其它GARCH結構相比，EGARCH模型可更好對收益率的波動特性進行描述，具有較強的預測性能。此外，由圖2或圖3可發現，采用MSE和MAE作為度量指標，IGARCH的預測性能將高于EGARCH；但以MAPE和HMSE作為指標時，則不盡然。利用OLS策略將MAPE和HMSE的預測績效作對比，我們發現4種代價函數的相對績效并無顯著差異，回歸檢驗的p值分別達到0.324（MSE）、0.716（MAE）、0.430（MAPE）和0.362（HMSE），均高于顯著性水平0.02。因此，可認為EGARCH和IGARCH模型的預測性能并無明顯差異性。

4 結論

本研究從波動性預測的視角，采用一種半參數方法——估計函數策略進行參數估計。由于金融資產的收益率往往呈現出顯著的傾斜性和超額峰度，估計函數策略在進行參數估計時加入了一些高階矩信息，使得比QMLE的估計更為高效。另外，在進行績效評估時，傳統的代價函數排序法難以提供統計意義下的檢驗結果，且可能存在“數據窺察”問題，本文采用最小二乘（OLS）方法對預測模型進行檢驗。實證分析結果表明，在高斯分布的條件下，形式最精簡的積分GARCH（IGARCH）模型具有較優的預測性能。盡管如此，基于EF策略的預測結果表明，指數GARCH（EGARCH）的預測能力更為優越。主要是因為EF策略具有更佳的估計效率，因此，與其它GARCH類模型相比，本文得出EGARCH模型可更好地描述金融資產收益率的波動過程。

[1]林德欽.創業板指數波動率預測效果比較研究——基于GARCH族模型[J].金融教學與研究,2014,(1).

[2]王鵬，呂永健.基于不同記憶性異方差模型的中國股票市場波動率預測[J].中國管理科學,2013,(S1).

[3]吳曉雄.我國燃油期貨市場的波動率預測模型[J].統計與決策,2013,(14).

[4]楊科，田鳳平.農產品期貨市場波動率的動態特征及其預測模型[J].經濟評論,2014,(4).

[5]周偉峰，向華.權證和其標的資產波動率的相關性分析[J].重慶工商大學學報(自然科學版),2014,(1).

[6]楊繼平，袁璐，張春會.基于結構轉換非參數GARCH模型的VaR估計[J].管理科學學報,2014,(2).

[7]高艷超.GARCH模型、非參數GARCH模型及SV模型的比較綜述[J].現代商業,2012,(29).

[8]方立兵，郭炳伸，曾勇.GARCH族模型的預測能力比較:一種半參數方法[J].數量經濟技術經濟研究,2010,(4).

[9]李翠霞，郭二林，包美娟.一種帶有自權重的積分波動率的非參估計[J].中山大學學報(自然科學版),2013,(1).

[10]房小定.基于GARCH族模型族的創業板指數波動性研究[J].金融經濟,2014,(8).